《Codes With Local Regeneration and Erasure Correction》论文解读
首先确立自己读这篇论文期待收获什么：
1. 最重要的：懂作者如何将Local 和 Regeneration结合，通过什么样的方法，得到了什么样的结果
2. 理清作者的写作思路，尽量看懂作者引经据典的背后代表了什么
然后分析论文的结构和过程，看看作者是怎么写的：
1. 先从局部性出发，介绍什么是Locally Repair Code，自己也要理解什么是局部修复码，是怎么实现的
2. 在论文的Ⅱ：Scalar Codes With Locality 部分，作者先介绍了（r，δ） Codes Symbol Locality，再深入下去，Information Locality。
（r，δ） Codes Symbol Locality，参考导师毕业论文，
Codes With(r,δ)-Locality：一个LRC的定义是要求每个码符是一个长度不 超过r+1的单校验码的一部分。如果将这个要求替换为：每个码符是一个 [r+δ−1,r, δ]MDS码 的一部分，那么这样的码就是一个具有(r,δ)局部性的码。更加具体地说，一个Fq上具有(r,δ)局部性的码C是一个Fq上的[n,k] 线性码且满足对于每一个码符ci，存在一个索引集S i⊆[n]使得 dm in(C|Si)≥δ 且|Si|≤ r+δ−1，其中C|Si是这个线性码限制在索引集Si下的码，dmin(·)是最小汉明距离。具有(r,δ)局部性的LRCs也分为具有(r,δ)-ISL的LRCs和具有 (r,δ)-ASL的LRCs。在文献[64]中，Prakash等人类似地给出了具有(r,δ)-ISL 的LRCs的最小汉明距离的上界：
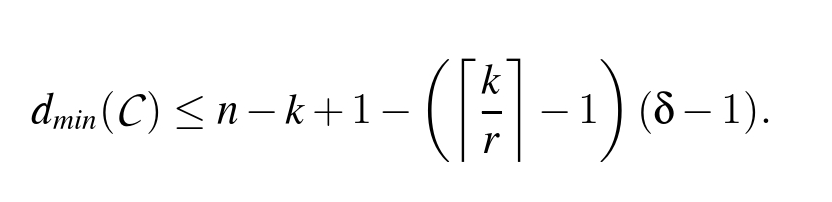
具有(r,δ)局部性且满足上述等式约束的码称为最优的。
上述汉语已经说的比较清楚，先不管是中间是怎么做的，得到的 每个码符是一个[r+δ−1,r, δ]MDS码的一部分，那么这样的码就是一个具有(r,δ)局部性的码；也满足上述图片中的不等式。
2024-4-17日记
在第二部分，通过金字塔码，推导出了singleton-like Bound，同时通过金字塔码也理解了r和δ的含义，接下来详细阐述。
同时也有几个问题，先列举出来，后面逐一解决。
1.是怎么和punctured code扯上关系的，punctured code我理解，但是locally code我不理解
2.金字塔码理解以后，关于它举的例子我不理解是什么意思
接下来介绍金字塔码：
首先：“Consider an [n′ , k, dmin] systematic MDS code over Fq ,where n′ = k + dmin − 1”，所以就有生成矩阵G = （Ps：这一步应该能理解，就是通过k和dmin来确定n'，然后抽象上构建一个G，G是生成矩阵，所以就满足生成矩阵的形式，左边是单位矩阵，右边是Q矩阵）
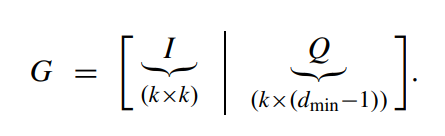
然后：Let k = xr + y, with 0 ≤ y ≤ (r − 1). First the matrix Q is partitioned into submatrices as shown below:（矩阵Q被划分为子矩阵，如下所示）（Ps：这一步应该也能理解，就是再细分，把Q细分成下面的形式）
Qi是r ×(δ−1)
Qx+1 是y ×(δ −1)
Q ′ 是k ×(dmin −δ)
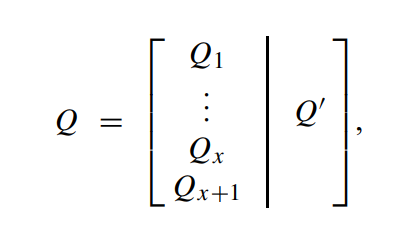
所以，左边Q1~Qx+1形成的矩阵是(rx+y) × (δ−1)，右边的矩阵是k×(dmin −δ)
再然后：“consider a second generator matrix G ′ obtained by splitting the first (δ − 1) columns of Q as shown below:”(通过分割Q的前 (δ − 1) 列，来获得第二个生成矩阵G')（Ps，其实就是把上面Q1~Qx+1，斜着写，组成的矩阵）
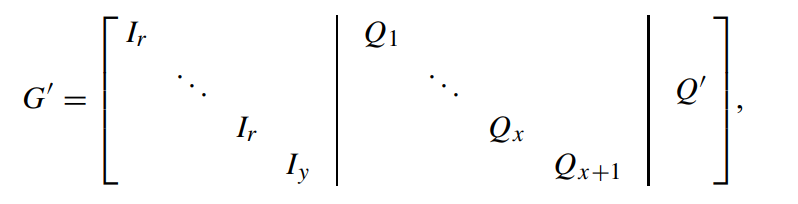
那么此时，G‘是多少行多少列呢？我们来计算一下：左边是I单位阵，根据G可知，左边是k×k（也可以写成rx+y，前面也说了，满足k = xr + y，所以此处也可以写成k×k）；中间的Q1~Qx每一个都是r ×(δ−1)，那么一共就有rx行，(δ−1)x列，再加上Qx+1，那么就是rx+y行，(δ−1)x+(δ−1)列，整理一下得，k行(δ−1)(x+1)列；右边Q’满足 k ×(dmin −δ)；综上，G‘是k行(k+(δ−1)(x+1)+(dmin −δ))列，同时G’也是k×n满秩矩阵，那么我们可以讲两者等价，即 n = (k+(δ−1)(x+1)+(dmin −δ))，将x用k和r表示，由k = xr + y得x = ⌈k/r⌉-1，得n = k + dmin +(⌈k/r⌉-1)(δ−1)，即满足：
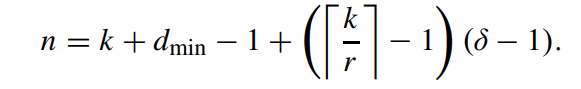
但是作者举例说明时，我对例子不理解
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
接下来是Ⅲ部分，Vector Codes，矢量编码的理解
主要还是偏向数学上的理解，我通过Google和OPENAI的人工智能，浅显的了解了一下：
