LRC codes理解
之前看了再生码的相关文献,大概知道了再生码的由来,也知道了两种trade off下的结果,且LRCs是针对RG codes来解决部分问题的。(2025年1月6日:这段描述是错误的,LRC不是针对再生码解决问题,LRC和RGC是平行的关系,甚至LRC比RGC更早提出和更多应用,无论是LRC或者RGC,都是解决分布式存储系统中的数据收集和数据修复问题,之前的修复是通过MDS性质重构数据节点,再通过重构出的数据节点替换失败节点完成,这样浪费了大量的带宽资源,LRC通过局部性解决该问题,RGC通过子分组解决该问题。)
LRC codes最根本的是要解决再生码修复过程中的修复度问题(利用局部性Locally来解决)。
------------------------------------------------------------------
Regeneration codes
存储开销和修复开销的关系:当码率越大,存储空间的效率越高,修复需要的数据量越大。(从定性分析的角度考量)
然后A.G.Dimakis等人首次利用信息流图推导出存储开销与修复开销满足以下(这个不等式之前也提到过):
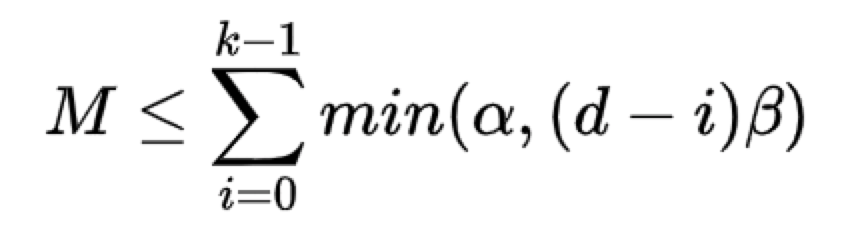
存储开销是所有节点存储量的总和:n×α
修复开销是所有参与修复的存储节点所需要传输的数据量:d×β
----------------------------------------------------------------------
LRC codes
接下来是说(n,k,r)LRC码的一些参数意义:
n:线性码中码长(总结点个数)
k:线性码中数据位的位数(数据节点个数)
r:如果是再生码中,这个r就是d(连接节点的个数),但是在LRC码中,r有不一样的含义,此处的r代表了“如果一个[n,k]线性码中的一个码符的值可以通过访问最多r个其他的码符来恢复,那么这个码符就具有修复局部性r(简称为r-locality)。具有修复局部性的码就称为局部可修复码(LRCs)。”,自己理解:修复一个码符时,需要借助r个其他的码来恢复该码符。
在论文《Codes with minimum bandwidth cooperative local regeneration》中的A部分,有提到(r,δ)-LRC,此处引入(r,δ)-LRC的目的是(在导师博士毕业论文中也有提到)“如果故障节点仅存在一个局部性为r的修复集,那 么如果这些r个节点中的一个也失效,则不能再通过只访问这r个节点来恢复故障的节点。换句话说,r-locality只能容忍一个节点故障。
引申出来的就有很多的研究细节问题:
1、单个节点修复(单次只修复单个节点)
2、多个节点修复(一次多个节点修复)
3、.......
另一方面来说,界(bound)就非常关键,因为界是衡量该码性能的标准,理解各个界(并且推导各个界)就是非常重要的课题。
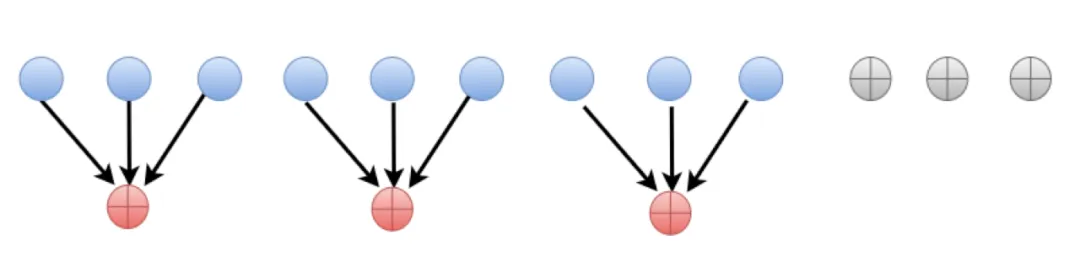
LRC码修复如图:
------------------------------------------------------------------------------
LRC码的最小距离满足上界如下:
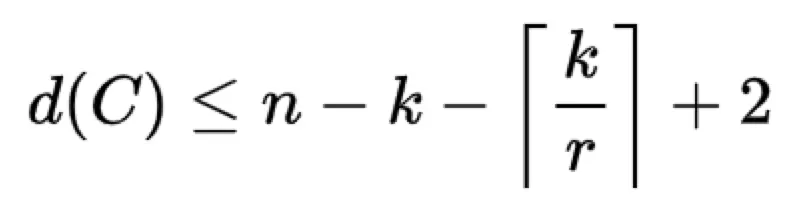
接下来证明这个上界怎么来的【论文《On the Locality of Codeword Symbols》】:
参考知乎文章:https://zhuanlan.zhihu.com/p/610398954
(我看不懂证明,希望以后能理解吧!再回来写怎么推导出来的)

2025年1月6日 补充:慢慢补足且学习上面的证明过程:
1、一个(n,k,d) 线性码中,通过最小距离d,我们可得:码字中任意d-1个错误都可以恢复,然而一旦有d个错误,数据无法恢复。(纠删码最多容忍d-1个数据块的丢失)
如何理解?我们要抓住最小距离深入分析,最小距离d意味着存在两个码,他们之间有d个符号不同,假设两个码中的一个码,它的d-1个码符出错,我们通过该码字的最小距离d,可以通过出错后的码符重新计算出错误位,从而完成数据恢复。
举个例子说明:(n=7,k=4,d=3)Hamming Code,根据 d-1=2得:最多容忍2个错误。其生成矩阵为:
1 0 0 0 0 1 1 0 1 0 0 1 0 1 G = [ 0 0 1 0 1 1 0 ] 0 0 0 1 1 1 1
假设原始信息为m =[1,0,1,1],根据生成码字c = m· G 得: c = [1,0,1,1,0,1,0]。
现在假设两位出错,不妨设第2位和第6位出错,即生成码字c = [1,*,1,1,0,*,0],现在我们利用生成矩阵和剩余的5个符号进行恢复。
设原始信息m = [m1,m2,m3,m4],c=[c1,c2,c3,c4,c5,c6,c7]是生成码字,则有:
c2 = m2,c6 = m1+m3+m4,我们可以通过已知的符号c1,c3,c4,c5,c7建立以下线性关系:
c1 = m1 = 1
c3= m3 = 1
c4 = m4 = 1
c5 = m2+m3+m4 = m2+1+1 =m2 = 0
c7 = m1+m2+m4 = 1 +m2+1 = m2 = 0
因此 c2= m2 = 0
c6 = m1+m3+m4 = 1+1+1 =1
因此成功恢复丢失数据。
若按照上述例子,假设发生d=3个错误,我们尝试完成恢复。
假设在c2和c6出错基础上,c1也发生错误,我们能得到如下的线性关系:
c3= m3 = 1
c4 = m4 = 1
c5 = m2+m3+m4 = m2+1+1 = 0 => m2=0
c7 = m1+m2+m4 = m1+m2+1=0 => m1+m2=1 => m1=1
因此,通过c5和c6的线性关系可得,m1 = 1,m2=0,而c1=m1=1,c2=m2=0,c6=m1+m3+m4 = 1+1+1=1
---------------------------------------------------------------------------------
上述的局部修复码只能修复一个故障节点,针对多个故障节点的LRC修复,引入了(n,k,r,δ)-局部修复码,针对多个故障节点修复的局部修复码满足上界如下:
![]()
接下来也证明这个不不等式【《On the Locality of Codeword Symbols》和《Codes With Local Regeneration and Erasure Correction》】。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号