Decomposition——HDU7028

Decomposition

https://acm.hdu.edu.cn/showproblem.php?pid=7028

题目大意

给出 \(n\)个点的完全无向图，和长度为 \(k\)的序列 \(l\)，现要求将从完全图中取出 \(k\)条路径，第\(i\)条路径长度为 \(l_i\)，并且每条路径中不存在重边，输出每条路径。

解题思路

考虑欧拉回路的构造，即我们只要构造出一条包含 \(n\)个点欧拉回路，因为 \(n\)个点的欧拉回路保证连续 \(n+1\)条边才会出现重边，而题目 \(l_i \leq n-3\)，故欧拉回路可以满足题意。
然后固定起点，将第 \(2\)个点依次从剩下的\(n-1\)个点中取即可。这样我们总共会得到 \((n-1)n\) 条路径，满足题意中的总路径数量，所以只需要求出这 \((n-1)\)条欧拉回路即可。

欧拉回路的构造应该有很多种方法，现列出一种：
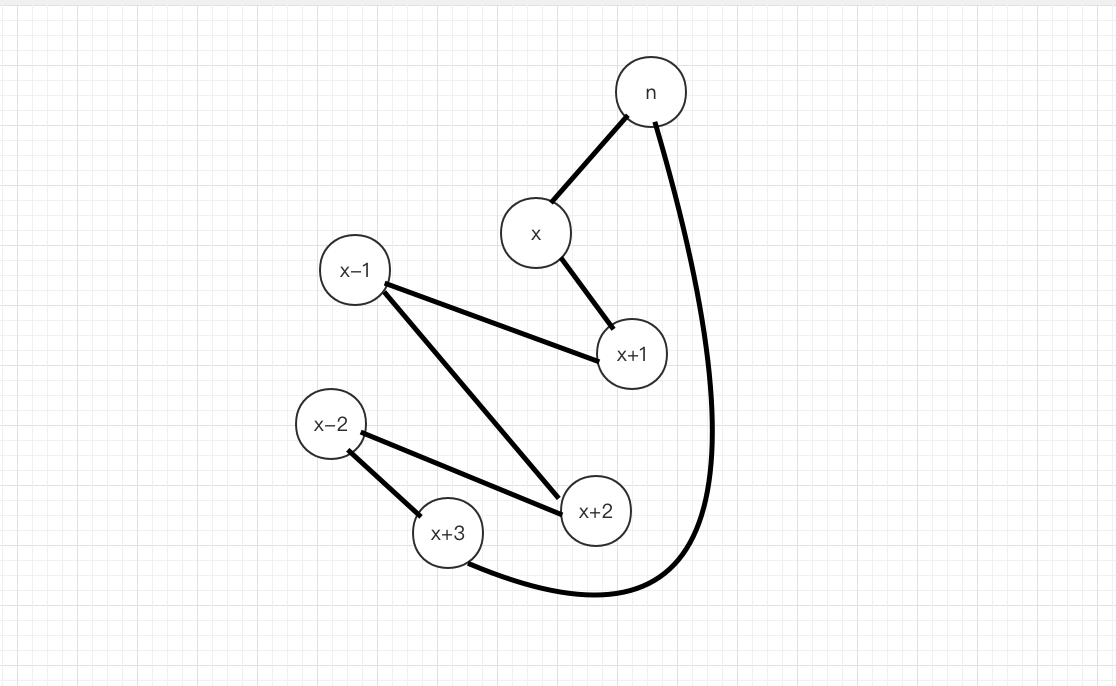
固定起点为 \(n\)，设与起点相连的点为 \(x\)，则我们可以构造这样一个序列：\(n,x,x+1,x-1,x+2,x-2,\cdots,n\)，后面在改变 \(x\)依照上式求即可。（注意此时的减\(1\)和加\(1\)是在模\((n-1)\)的意义下计算的）如下图。

Code

#include <bits/stdc++.h>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
#define fi first
#define se second
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define pb push_back
#define V vector
using namespace std;
const int N = 2e5 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
int a[N],tot;
void solve(){
	int n,k;
	cin >> n >> k;
	for(int i = 1; i <= k; i++){
		cin >> a[i];
	}
	V<int>v;
	v.pb(n);
	for(int i = 1; i < n; i++){
		int k = (i - 1 + n - 1) % (n - 1);
		if(k == 0)k = n - 1;
		v.pb(i);
		int cnt = 0;
		for(int j = i + 1; cnt < n - 2; ){
			v.pb(j);
			j = (j + 1) % (n - 1);
			if(j == 0)j = n - 1;
			if(++cnt == n - 2)break;
			v.pb(k);
			k = (k - 1 + n - 1) % (n - 1);
			if(k == 0)k = n - 1;
			++cnt;
		}
		v.pb(n);
	}
	int p = 0;
	cout << "Case #" << ++tot <<":\n";
	for(int i = 1; i <= k; i++)
	{
		a[i]++;
		for(int j = 1; j <= a[i]; j ++){
			cout << v[p++];
			if(j == a[i])cout << "\n";
			else cout << " ";
		}
		p--;
	}
}

int main()
{
	#ifdef ONLINE_JUDGE
	#else
		freopen("in.txt", "r", stdin);
		freopen("out.txt", "w", stdout);
	#endif

	qc;
	int T = 1;
	cin >> T;
	while(T--){
		solve();
	}
	return 0;
}