搜索
-
定义
套用一下OI wiki上的定义，搜索，也就是对状态空间进行枚举，通过穷尽所有的可能来找到最优解，或者统计合法解的个数。
不难看出，所谓搜索，本意上就是依靠自己对题目状态转移的理解进行枚举。
-
Lead-inⅠ
既然搜索本质是暴力，那我们为什么常用搜索而不常用暴力呢？
以全排列问题为例，对于\(n=3\)时，我们可以显然地用三重循环解决问题，那当\(n=4\)时呢？我们大可以再加一个特判写一个四重循环，那么我一直加下去，一直加到\(n=100\)呢？这时候显然无法枚举。对于这种无法用简单的思路进行枚举时，我们就可以进行搜索。
tips：或许你也可以这么理解，对于图和树，我们并不清楚他们的结构（至少在我们写代码时并不清楚），这种情况下枚举也是无法使用的。
-
DFS
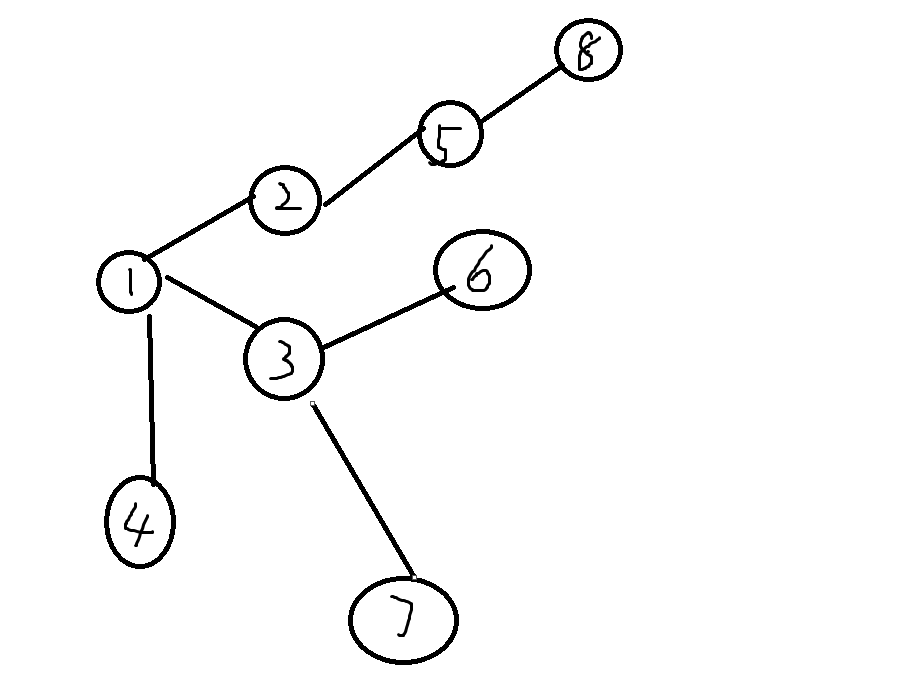
让我们来康康这个图，如何解释DFS的思路呢？就是一条路走到底。
DFS的搜索过程大体概括，就是一条路走到黑，走到头之后从后向前回溯更新结果，所以起点位置对应的ans即为此条路径的ans。
让我们来深究一下其原理，我们搜索每一个节点时枚举这个节点通往的所有节点，然后选取第一个进行搜索。
也就是说DFS形成了一个FILO（先进后出）结构，也就是栈。（至少tarjan理解返祖边时应该理解过dfs是栈的概念）。
DFS实现的代码（by Kazdale）
#include <iostream>
using namespace std;
int r,c,ans=0;
int map[120][120];
int xx[4]={0,1,0,-1};
int yy[4]={1,0,-1,0};
int temp[120][120];
int dfs(int x,int y){
if(temp[x][y]){
return temp[x][y];
}
int maxn=1;
for(int i=0;i<4;i++){
int dx=xx[i]+x;
int dy=yy[i]+y;
if(dx>=1&&dx<=r&&dy>=1&&dy<=c&&map[dx][dy]<map[x][y]){
maxn=max(maxn,dfs(dx,dy)+1);
}
}
temp[x][y]=maxn;
return maxn;
}
int main(){
ios::sync_with_stdio(false);
cin >> r >> c;
for(int i=1;i<=r;i++){
for(int j=1;j<=c;j++){
cin >> map[i][j];
}
}
for(int i=1;i<=r;i++){
for(int j=1;j<=c;j++){
ans=max(ans,dfs(i,j));
}
}
cout << ans << endl;
return 0;
}
-
BFS
BFS的思路是什么呢，就是我先走我先看到的节点。
BFS的搜索过程是将全部节点按照从起点向外的顺序都搜一遍，好处是只搜一遍，而劣势也十分明显，就是如果情况众多会造成大量的时空浪费。
在BFS中，我们枚举枚举这个节点通往的所有节点并将其放到缓存里。
这样形成了应该FIFO（先进先出），也就是队列。
tips：DFS和BFS的代码实现不难，这里就不放了，OI wiki自取。
BFS实现的代码（by Kazdale）
#include <iostream>
#include <cstring>
#include <queue>
#include <iomanip>
using namespace std;
int xx[]={1,-1,2,-2,2,-2,1,-1};
int yy[]={2,2,1,-1,-1,1,-2,-2};
int main(){
int n,m;
ios::sync_with_stdio(false);
cin >> n >> m;
int sx,sy;
cin >> sx >> sy;
int map[500][500];
memset(map,-1,sizeof(map));
queue<int>x;
queue<int>y;
queue<int>s;
x.push(sx);
y.push(sy);
s.push(0);
map[sx][sy]=0;
while(!x.empty()){
for(int i=0;i<8;i++){
int nx=x.front()+xx[i];
int ny=y.front()+yy[i];
if(nx<=n&&ny<=m&&nx>=1&&ny>=1&&map[nx][ny]==-1){
map[nx][ny]=s.front()+1;
x.push(nx);
y.push(ny);
s.push(s.front()+1);
}
}
x.pop();
y.pop();
s.pop();
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout << left << setw(5) << map[i][j];
}
cout << endl;
}
return 0;
}
-
两者的区别
有明确起始点时DFS会更好用，而求终节点时BFS更好用。
-
Lend-inⅡ
按理说，对于大部分问题，其逻辑都可以转化为一个DAG。
那么，对于一个有\(n\)个点，\(m\)条边的DAG，其复杂度达到了令人感叹的\(O(n^m)\)。
这显然是十分夸张的，所以我们需要优化搜索。
-
不换汤也不换药的优化
字面意思，这里是一些不换汤也不换药的优化。
这东西可能有个更好的名字，叫防卡常技巧。
这里就不细讲了，因为跟搜索算法的思路无关（但是你平时要是写搜索很难不碰见它），这是传送门。
-
换汤不换药的优化
简单来讲，就是你不用重构你dfs或者bfs函数的优化。
- 最优性剪枝
如果当前状态下不可能出现最优解时，进行剪枝。（往往出现于当前的最优解比整体最优解劣时）
一般的实现方式是考虑当前情况一直进行最优决策玉当前最优解的对比，剪去重复的情况或者推算出上下界。
- 可行性优化
如果当前状况违法时，剪枝。
- 二分查找
如果搜索函数中出现枚举找单点的代码，使用二分查找来优化，能优化一个\(log\)的复杂度。
信仰剪枝
如果执行时间逼近时限了，直接输出当前的最优解。（并不正确，只能让你的TLE多了几分AC的概率）- 例题：P1120 小木棍
暴搜的实现代码（by Amb1ti0n）
//dfs(int k,int last,int rest) 在拼第k根原来的长棍,使用的上一根短棍长度,目前还有多少长度
#include<bits/stdc++.h>
using namespace std;
int n;
int m;
int a[66];
int nxt[66];//nxt[i] = 与i长度相等的木棍最后一根在()的位置上
int cnt,sum,len;
bool used[66];
bool ok;
inline int read()
{
int x = 0;
bool f = 1;
char c = getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f = 0;
for(;isdigit(c);c=getchar()) x = (x<<3)+(x<<1)+c-'0';
if(f) return x;
return -x;
}
bool cmp(int a,int b)
{
return a>b;
}
void dfs(int k,int last,int rest)
{
int i;
if(!rest)//未拼长度为0,下一根
{
if(k==m)
{
ok = 1;
return;
}
for(i=1;i<=cnt;i++)
{
if(!used[i]) break;
}//找到一根没用过的
used[i] = 1;
dfs(k+1,i,len-a[i]);
used[i] = 0;
if(ok) return;
}
//二分查找木棍长度不大于rest
int l =last+1;
int r = cnt;
int mid;
while(l<r)
{
mid = (l+r)>>1;
if(a[mid]<=rest) r =mid;
else l =mid+1;
}
for(i = l;i<=cnt;i++)
{
if(!used[i])
{
used[i] = 1;
dfs(k,i,rest-a[i]);
used[i] = 0;
if(ok) return;
if(rest==a[i]||rest==len) return;//若出现此种情况,证明此处操作无错,即前置操作有错 所以return
i = nxt[i];//直接跳到next[i] 省去部分步骤
if(i==cnt) return;//到头了
}
}
}
int main()
{
n = read();
int d;
for(int i=1;i<=n;i++)
{
d = read();
if(d>50) continue;//重要
++cnt;
a[cnt] = d;
sum+=d;
}
sort(a+1,a+cnt+1,cmp);//从大到小
nxt[cnt] = cnt;
for(int i=cnt-1;i>0;i--)
{
if(a[i]==a[i+1]) {nxt[i]=nxt[i+1];}
else nxt[i] = i;//预处理
}
for(len = a[1];len<=sum/2;len++)
{
if(sum%len!=0) continue;
m = sum/len;
//m 指段数
ok = 0;
used[1] = 1;
dfs(1,1,len-a[1]);
used[1] = 0;
if(ok)
{
printf("%d\n",len);
return 0;
}
}
printf("%d\n",sum);
return 0;
}
-
换汤换药的优化
-
折半搜索Meet in the middle
将一整个搜索流程分为两部分，从初始状态和末状态同时开始搜索，两边相遇即为解。
一般折半搜索可以将时间复杂度从\(O(n^m)\)降到\(O(n^{\frac{m}{2}})\).
折半搜索的实现代码（by ncwzdlsd）
#include <bits/stdc++.h>
using namespace std;
#define int long long
// 对于此题的两次 DFS 来说，要统计 1 个 sum（当前消耗钱数）和 pos（已经搜到哪里了）
const int maxn=1<<25;//左移 25 位相当于 2 的 25 次方
int q1[maxn],q2[maxn],co[45],ans,N,M,cnt1,cnt2,mid;
void dfs1(int sum,int pos)
{
if(sum>M) return;
if(pos>mid) {q1[++cnt1]=sum;return;}
dfs1(sum+co[pos],pos+1);
dfs1(sum,pos+1);//考虑不选当前位，继续向下搜
}
void dfs2(int sum,int pos)
{
if(sum>M) return;
if(pos>N) {q2[++cnt2]=sum;return;}
dfs2(sum+co[pos],pos+1);
dfs2(sum,pos+1);
}
signed main()
{
cin>>N>>M;
mid=(N+1)/2;
for(int i=1;i<=N;i++) cin>>co[i];
dfs1(0,1);
sort(q1+1,q1+cnt1+1);
dfs2(0,mid+1);
for(int i=1;i<=cnt2;i++)
ans+=upper_bound(q1+1,q1+cnt1+1,M-q2[i])-q1-1;
// cout<<cnt<<endl;
// cout<<N/2<<endl;
cout<<ans;
return 0;
}
-
记忆化搜索
顾名思义，将每个情况下的对应答案记录下来进行大量剪枝的搜索方式。
相当玄妙，因为改完记忆化之后爆搜代码会变得很像DP的代码。
同时，当你找到状态转移方程而不知道如何进行枚举时，也可以写记忆化搜索。
记忆化搜索有两种方式：
记忆化搜索的实现代码（by Steven24）
#include<bits/stdc++.h>
using namespace std ;
const int N = 1001 ;
int w[N] , c[N] ;
int mem[N][N] ;
int n , t ;
int dfs( int x , int left ){
if( mem[x][left] != -1 )
return mem[x][left] ;
if( x == n + 1 ){
mem[x][left] = 0 ;
return 0 ;
}
int dfs1 = 0 , dfs2 = 0 ;
dfs1 = dfs( x+1 , left ) ;
if( left >= w[x] )
dfs2 = dfs( x+1 , left - w[x] ) + c[x] ;
mem[x][left] = max( dfs1 , dfs2 ) ;
return mem[x][left] ;
}
int main () {
scanf("%d%d" ,&t ,&n ) ;
for( int i = 1 ; i <= n ; ++i )
scanf("%d%d",&w[i] ,&c[i] ) ;
memset( mem , -1 , sizeof(mem) ) ;
printf("%d" ,dfs( 1 , t ) ) ;
return 0 ;
}
-
A*
在我们使用BFS的时候，我们常常注意到这个算法选择了大量不会被选择的情况。
下图中将BFS（左）与正常人思考的方式进行对比。
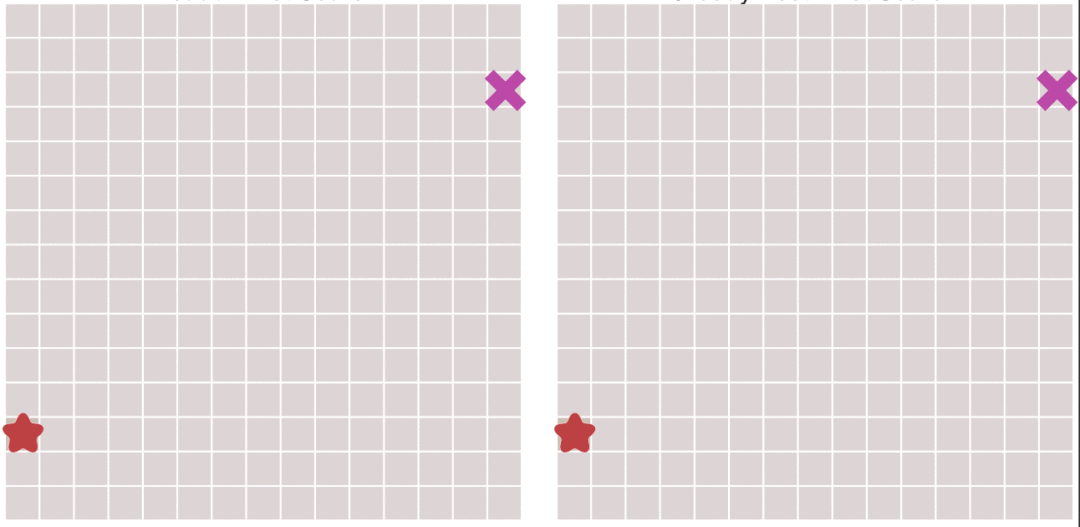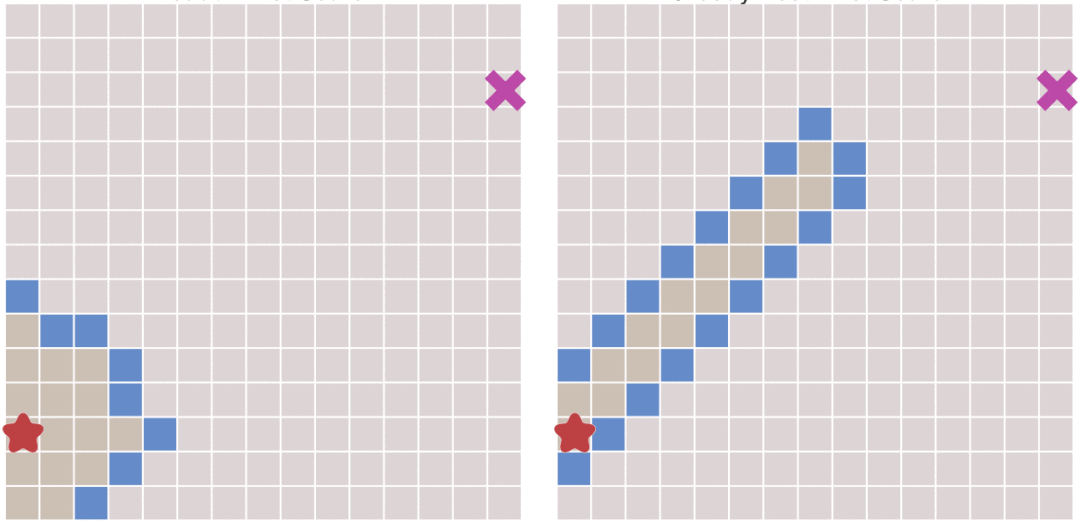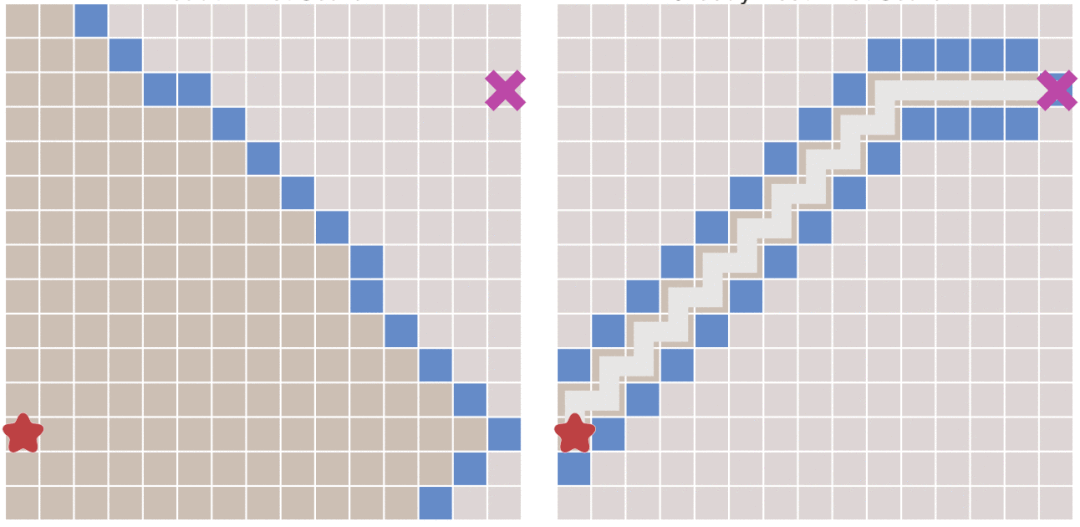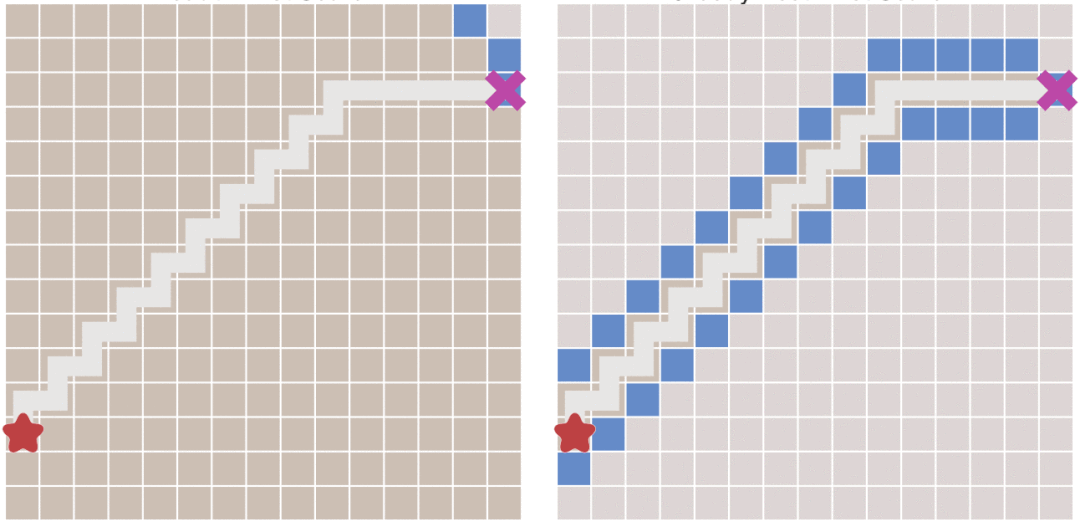
当我们在\(x\)且起点为\(0\)终点为\(n\)时，我们设我们从头到尾的总代价是\(f(x)\)，我们用一个\(g(x)\)记录\((0\) ~ \(x)\)的最短路，另外用一个\(h(x)\)记录\((x\) ~ \(n)\)的最短路。
我们可以简单地不断维护\(g(x)\)，但我们无法得出\(h(x)\)的准确值，我们需要估计它的值，所以它被称为估价函数。
估价函数的选择是我们自己决定的，但是有一个必须遵守的规矩。
我们设\((x\) ~ \(n)\)实际上的最短路为\(h*(x)\)，那么当算法保持正确性时，必有\(h(x)\leqslant h\!*(x)\)
证明过程
而\(h(x)\)越接近\(h*(x)\)，那么时空复杂度就越优秀，所以我们要谨慎选择\(h(x)\)
比如上面的gif中，\(h(x)\)就可以选为两点间的曼哈顿距离，当两点间无障碍物时，就有\(h(x) = h\!*(x)\)，若有障碍物，那么\(h(x) < h\!*(x)\)
显然，若有\(f(x) = g(x) + h(x)\)，那么\(f(x)\)就是在\(x\)点时从起点到终点的最短路，我们可以运用堆优化不断取出最小值像Dijkstra一样优化附近的点（实际上Dijkstra就是一种特殊的A*）
A*的代码实现（by Kazdale）
#include <iostream>
#include <algorithm>
#include <queue>
#include <set>
using namespace std;
int fx, fy;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
struct matrix {
int a[5][5];
friend bool operator < (matrix x, matrix y) {
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
if (x.a[i][j] != y.a[i][j])
return x.a[i][j] < y.a[i][j];
return false;
}
}f, st;
int h(matrix a) {
int cnt = 0;
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
if (a.a[i][j] != st.a[i][j])
++cnt;
return cnt;
}
struct node {
matrix a;
int t;
friend bool operator < (node x, node y) {
return x.t + h(x.a) > y.t + h(y.a);
}
}x;
priority_queue <node> q;
set <matrix> s;
int main() {
st.a[1][1] = 1, st.a[1][2] = 2, st.a[1][3] = 3;
st.a[2][1] = 8, st.a[2][2] = 0, st.a[2][3] = 4;
st.a[3][1] = 7, st.a[3][2] = 6, st.a[3][3] = 5;
for (int i = 1; i <= 3; ++i) {
for (int j = 1; j <= 3; ++j) {
char c;
cin >> c;
f.a[i][j] = c - '0';
}
}
q.push({f, 0});
while (!q.empty()) {
x = q.top();
q.pop();
if (!h(x.a)) {
cout << x.t << endl;
return 0;
}
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
if (!x.a.a[i][j]) fx = i, fy = j;
for (int i = 0; i < 4; ++i) {
int xx = fx + dx[i], yy = fy + dy[i];
if (xx >= 1 && xx <= 3 && yy >= 1 && yy <= 3) {
swap(x.a.a[fx][fy], x.a.a[xx][yy]);
if (!s.count(x.a)) {
s.insert(x.a);
q.push({x.a, x.t + 1});
}
swap(x.a.a[fx][fy], x.a.a[xx][yy]);
}
}
}
return 0;
}
