MIT 6.S081 Lab Allocator 聊聊buddy allocator

前言

Lab Allocator代码量很少，主要是用xv6已经写好的buddy allocator替换掉kallocator。kallocator简单的将内存分为4096bytes（下简称PGSIZE）页面，将空闲页面串接成双向链表。这种方式很简洁，可以很好的应用First Fit算法，且没有用多余的数据结构去管理内存。但一次只能分配完整的一页。buddy allocator可以灵活的分配2^k * LEAF_SIZE字节的内存，且分配和回收的时间复杂度并不高，是一种很优良的内存分配算法。

 

尽管如此，我个人并不认为在内核上使用buddy_allocator是一种比较好的方法，让内存去管理这么多的小内存块是极不理智的。假如我们真的要在xv6上开发用户程序，我们也肯定不是通过sbrk去请求堆空间，而是通过user/umalloc.c下提供的api来请求堆内存。使用umalloc.c提供的api时，如果调用free(ptr)，进程并不会调用sbrk去消除堆内存，而是将这块空间存放到自己的freelist中。当进程下次请求堆空间时会首先查看freelist，如果空间足够就不再调用sbrk向内核请求堆空间。

由于xv6并没有实现内存置换算法，因此进程申请的内存只能等到进程结束时被内核回收。很明显，相比于直接将buddy allocator应用到内核上，更明智的方法是把buddy allocator应用到user/umalloc.c下，进程仍然一次向内核请求完整的一页，然后在umalloc.c下使用buddy allocator细化空间粒度。

不过既然Lab要求我们直接替换kallocator，那我们就不管它了。

 

项目已提供的buddy allocator路径为kernel/buddy.c。在本项目中我们要完成三个任务：

1) 使用buddy alloctor来管理空闲内存

2) 修改file.c下的ftable(系统文件表)，使系统最多可打开文件不再受NFILES的限制

3) 优化buddy allocator的空间消耗

 

buddy算法的执行过程不再赘述，如果不了解建议看一下wiki pedia：https://en.wikipedia.org/wiki/Buddy_memory_allocation

在这里感谢RedemptionC，强烈推荐关注他写的关于6.S081的blog：https://blog.csdn.net/redemptionc/category_10065273.html

 

本blog仅讨论buddy的实现和buddy空间的优化。

buddy的数据结构和初始化

struct sz_info {
  Bd_list free;　　　　　 // 空闲空间链表。
  char *alloc;　　　　　　// 用一个bit记录某个块是否被分配出去了
  char *split;　　　　　　// 用一个bit记录某个块是否发生了分裂
};
typedef struct sz_info Sz_info;

static Sz_info *bd_sizes;   // bd_sizes[k]记录了2^k * LEAFSIZE大小的块的分配信息

static void *bd_base; // start address of memory managed by the buddy allocator static struct spinlock lock

buddy_allocator首先需要一段连续内存来存放这些元数据。这段内存的大小可以根据buddy allocator所管理的内存地址范围高精尖海量算获得(曹曹草震怒.jpg)，我们下面重点分析一下bd_init完成alloc、split初始化的部分：

void
bd_init(void *base, void *end) {

  ......  

  nsizes = log2(((char *)end-p)/LEAF_SIZE) + 1;
  if((char*)end-p > BLK_SIZE(MAXSIZE)) {
    nsizes++;  // round up to the next power of 2
  }

  .....

  for (int k = 0; k < nsizes; k++) {
    lst_init(&bd_sizes[k].free);
    sz = sizeof(char)* ROUNDUP(NBLK(k), 8)/8;
    // sz = sizeof(char) * ROUNDUP(NBLK(k), 16)/16;
    bd_sizes[k].alloc = p;
    memset(bd_sizes[k].alloc, 0, sz);
    p += sz;
  }

  ......

  for (int k = 1; k < nsizes; k++) {
    sz = sizeof(char)* (ROUNDUP(NBLK(k), 8))/8;
    bd_sizes[k].split = p;
    memset(bd_sizes[k].split, 0, sz);
    p += sz;
  }
  p = (char *) ROUNDUP((uint64) p, LEAF_SIZE);

  ......
}

首先需要计算nsizes，即到底这段空间需要用多少"阶"的bd_allocator管理。阶的值直接确定了bd_sizes的长度。

当nsizes确定后，需要对每个"阶"(下面简称k)下的alloc、split进行分配。NBLK宏计算k阶下有多少个block可供分配，alloc、split均用一个bit标注这个block是否被分配/分裂，因此alloc、split所需空间大小均为 ROUNDUP(NBLK(k), 8) / 8。除以8是因为一个char可以用8个bit记录这些信息。

盗个图来大概展示一下buddy allocator下的内存布局，图片源于https://blog.csdn.net/RedemptionC/article/details/108012836

 

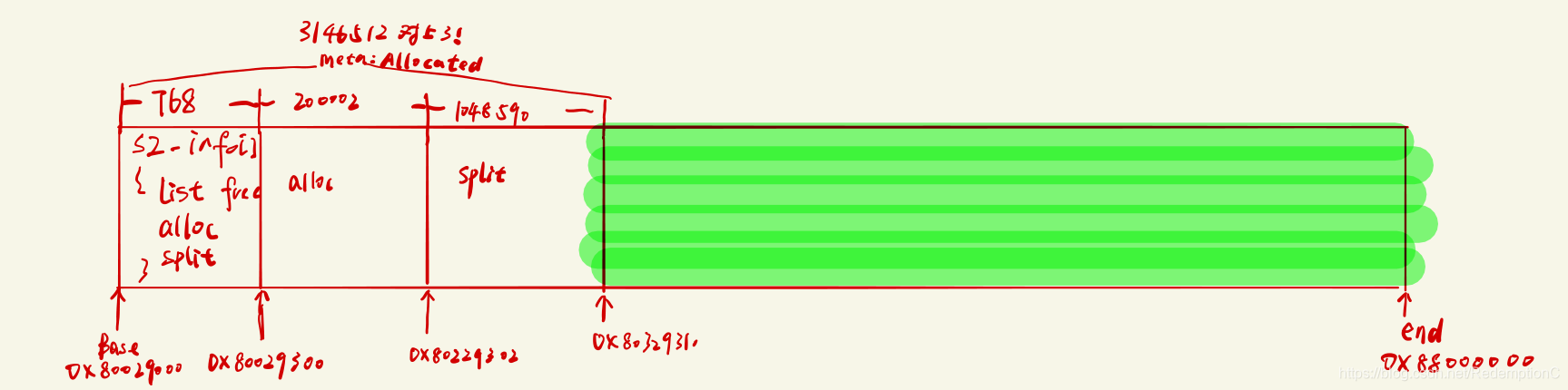
buddy的代码到目前为止还是非常亲民的，后面就越来越让人想锤墙(

标注已经分配和无法分配的空间

已经分配的空间其实就是分配给元数据的空间（元数据包括bd_sizes，bd_sizes[k].alloc，bd_sizes[k].split等）。这段空间从base开始，到执行完第二个for循环结束后的p终止。这段空间需要被我们标注为已分配：

void
bd_init(void* base, void* end) {
    .......
  int meta = bd_mark_data_structures(p);
  int unavailable = bd_mark_unavailable(end, p);
  void *bd_end = bd_base+BLK_SIZE(MAXSIZE)-unavailable;
  .......
}

int
bd_mark_data_structures(char *p) {
  int meta = p - (char*)bd_base;
  printf("bd: %d meta bytes for managing %d bytes of memory\n", meta, BLK_SIZE(MAXSIZE));
  bd_mark(bd_base, p);
  return meta;
}

我们要注意，当k阶的block被标注为已分配时，所有在这个block下，阶数小于k的block也必须要被标注为已分配。具体代码在bd_mark中，也不算太难看懂。

void
bd_mark(void *start, void *stop)
{
  int bi, bj;

  if (((uint64) start % LEAF_SIZE != 0) || ((uint64) stop % LEAF_SIZE != 0))
    panic("bd_mark");

  for (int k = 0; k < nsizes; k++) {
    bi = blk_index(k, start);
    bj = blk_index_next(k, stop);
    for(; bi < bj; bi++) {
      if(k > 0) {
        // if a block is allocated at size k, mark it as split too.
        bit_set(bd_sizes[k].split, bi);
      }
      bitset(bd_sizes[k].alloc, bi);
    }
  }
}

无法分配的空间可能比较难理解。如果最终的阶为nsizes-1，我们实际可以用buddy管理的空间大小为  ((1L << (nsizes - 1)) * LEAF_SIZE)，即buddy.c中定义的宏HEAPSIZE，而这个空间大小很可能已经超过了end - base的大小。因此我们必须将[end , HEAPSIZE)间的空间同样标注为“已分配”，来避免将这片空间分配出去。

下面讲讲buddy中最为迷惑的代码 bd_initfree。

bd_initfree

bd_initfree的代码非常简洁，但也非常晦涩难懂，比xv6中进程调度的代码还要难以理解。

int
bd_initfree(void *bd_left, void *bd_right) {
  int free = 0;

  for (int k = 0; k < MAXSIZE; k++) {   // skip max size
    int left = blk_index_next(k, bd_left);
    int right = blk_index(k, bd_right);
    free += bd_initfree_pair(k, left, bd_left, bd_right);
    if(right <= left)
      continue;
    free += bd_initfree_pair(k, right, bd_left, bd_right);
  }
  return free;
}

简单来看，bd_initfree的工作非常简单，就是将[left, right)所有的空间分割成不同阶大小的blocks，并将blocks的地址添加到相应阶下bd_sizes的free中。而如何将这些空间切割成连续的、buddy间不相邻的block是一个较为困难的问题。我们重点关注一下bd_initfree是怎么解决这个问题的。

首先我们注意到，同一个阶(假设为k)下的所有空闲的blocks间两两不能是buddy。如果存在两两是buddy的情况，那么这两个block应该是k+1阶下的某一个block。示意图如下：

bd_initfree针对这个问题，选择从空闲空间的两端开始收集空闲块，且每个阶下只收集至多两个空闲块。这样就不会出现空闲块间相邻且互为buddy的情况。

这样，同一阶下空闲块间不能为buddy的问题得以解决，但bd_initfree这种分配方法，真的能让所有空闲块在[bd_left，bd_right)间首尾相接么？会不会出现空闲块间覆盖的情况？

我们可以证明该算法可以让空闲块间首尾相接。

整个证明分为两部分：

 1）证明bd_initfree的for循环每完成一次，自bd_left开始到left的空闲块是连续的（左连续），自right开始到bd_right的空闲块是连续的（右连续）

 2)  存在某个阶数k，使得左连续的块和右连续的块在中间某处拼接起来

证明了1和2，即可证明[bd_left，bd_right)间所有的空闲block是首尾相接的。

第一个证明其实很简单，只要是按照步骤画一下图，即可很直观的看出。下图中红色表示空闲区，灰色表示非空闲区。最初始时bd_left的左侧是buddy allocator的元数据区域，bd_right的右侧是无法分配的区域，这两块区域均已被标记为“已分配”。虽然随着for循环的进行k越来越高，但仍然可以保持左连续这一性质：

 

上图中比较迷惑的是k=2,3时的情况。在上图的例子中我举的是特例，让k=2,3时互为buddy的块都包含了k=0时已分配的空间。因此相应的blocks不应被包含在freelist中，故在上图中被标为了灰色。

右连续可以由对称性导出，这样第一个证明是成立的。

第二个证明同样可以画图证得，也可以用数学更为严谨的证明。下图中是分配[9, 19)这一块空间时，k每次变动时添加到freelist的空间示意图：

我们设 k = K（K != 0）时，左侧已分配的block中下标最大的leaf下标为l_idx，右侧已分配的block中下标最小的leaf的下标为r_idx。如上图中，当k=2时，

l_idx=11，r_idx=16。

这样我们就证明了[bd_left，bd_right)间的块一定是左右相连的。

 

TODO:

最近时间非常紧，本blog潦草发布仅仅是为了和群友讨论一下buddy这块的算法，请见谅。