2018.11.04 练习赛
T1 【NOIP2018模拟】动态点分治
题面:
题目描述
CJK 是一个喜欢数据结构的同学。一天他看到 BZOJ 4012 这一题。“这似乎可以用动态点分治做。”, 他想。然而他并不会动态点分治,因此他拿着这一题去问 XXX。
然而 XXX 跟他说:“你呀,毕竟图样图森破,上台拿衣服!连基础都没学好,就想学这些高端的东西! 来,我这里有一题,如果你能把这道题秒掉,我才能教你动态点分治!”
于是 CJK 打开题目。题目很短,只有一句话:
“给出 l, r, k,请从小到大输出所有在 [l, r] 范围内,能表示为 k 的非负整数次方的所有数。”
“多组数据。”,XXX 补充说,“注意所有数的 0 次方都为 1,因此 1 也得算进去哦。”
输入描述
第一行一个数 T,表示数据组数。
接下来 T 行,每行 3 个数 l,r,k,表示一组数据。
输出描述
对于每一组数据输出一行(总共输出 T 行)。
如果存在符合要求的数,则在一行内从小到大输出这些数;否则输出一个字符串 "None."(包括句点,不包括引号)。
输入样例
4
1 10 2
2 4 5
19562 31702689720 17701
3680 37745933600 10
输出样例
1 2 4 8
None.
313325401
10000 100000 1000000 10000000 100000000 1000000000 10000000000
备注
对于所有数据,T ≤ 10000,l ≤ r,0≤ l,r,k < 2^63。
子任务 1(20 分):r - l ≤ 1000。
子任务 2(30 分):l, r, k < 2^31。
子任务 3(50 分):l, r, k < 2^63。
这里的子任务表示的是数据类型,并不捆绑测试。
三个子任务中,各有 10 分的数据,满足 T = 10 且数据是随机的。
特别注意:本题中 0 的 0 次方也看做 1。
题解:
暴力枚举,上限为\(\frac{r}{k}\),这样可以防止爆掉\(long、 long\),注意特判\(0/1\)即可;
\(code\):
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>
#include<ctype.h>
#include<vector>
#define ld double
#define ls p<<1
#define rs p<<1|1
#define mid (l+r>>1)
#define ll long long
using namespace std;
char buf[1<<20],*p1,*p2;
inline char gc()
{
// return getchar();
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin))==p1?0:*p1++;
}
template<typename T>
inline void read(T &x)
{
char tt;
bool flag=0;
while(!isdigit(tt=gc())&&(tt!='-'));
tt=='-'?(flag=1,x=0):(x=(tt^'0'));
while(isdigit(tt=gc())) x=(x<<1)+(x<<3)+(tt^'0');
if(flag) x=-x;
}
ll t,r,l,k;
int main()
{
read(t);
while(t--)
{
read(l),read(r),read(k);
if(k==0)
{
if(l==0&&k==0)
{if(r>=1) puts("0 1");
if(r==0) puts("0");
continue;}
if(l==1&&k==0){puts("1");continue;}
puts("None.");
continue;
}
if(k==1)
{
if(r==0) {puts("None.");continue;}
if(r>=1&&l<=1) {puts("1");continue;}
if(l>1) {puts("None.");continue;}
continue;
}
ll ans=1;bool flag=0;
while(ans<=r/k)
{
if(ans>=l)
printf("%lld ",ans),flag=1;
ans*=k;
}if(ans>=l&&ans<=r) printf("%lld",ans),flag=1;
if(!flag) puts("None.");
else puts("");
}
}
T2【NOIP2018模拟】区间
题意:
给一数列,求最长区间满足其中\(a_i\)为整个区间公因数,卡\(O(NlogN)\)算法;
题解:
如果写出一个\(O(N^2)\)的算法,就容易往下想出正解了;
发现对于某一位置\(x\),向右扩展的最大长度如果小于\(x-1\)位置就没什么大的用处了,直接设\(F[i]\)为\(i\)位置可以扩展的最大距离,然后用一只增不减的指针只要满足\(a[tail]%now==0\)就向前扫,扫完就记录\(F[i]=tail-1\);
对左边扫也是一样,最后取个最大值就行;
由于\(tail\)一直向前扫,数列中每个数只被遍历一次时间复杂度\(O(N)\);
\(code:\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>
#include<ctype.h>
#include<vector>
#define ld double
#define ls p<<1
#define rs p<<1|1
#define mid (l+r>>1)
#define ll long long
using namespace std;
char buf[1<<20],*p1,*p2;
inline char gc()
{
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin))==p1?0:*p1++;
}
template<typename T>
inline void read(T &x)
{
char tt;
bool flag=0;
while(!isdigit(tt=gc())&&(tt!='-'));
tt=='-'?(flag=1,x=0):(x=(tt^'0'));
while(isdigit(tt=gc())) x=(x<<1)+(x<<3)+(tt^'0');
if(flag) x=-x;
}
const int maxn=4*(1e6)+2;
int n;
ll a[maxn],f[maxn];
int main()
{
// freopen("B.in","r",stdin);
// freopen("B.out","w",stdout);
read(n);a[0]=-1;
for(int i=1;i<=n;i++) read(a[i]);
for(int i=1,j=1;i<=n;i++)
{
while(j<=n&&a[j]%a[i]==0) j++;
f[i]=j-1;
}
// for(int i=1;i<=n;i++)
// printf("%lld ",f[i]);
ll ans=0;
for(int i=n,j=n;i>=1;i--)
{
while(j>=1&&a[j]%a[i]==0) j--;
ans=max(ans,f[i]-j);
}
printf("%lld",ans);
}
T3 【NOIP2018模拟】灭虫
题意:
给\(N\)个点,每个点可以选择向左覆盖\([p-l,p]\)的区间,向右覆盖\([r,p+r]\)的区间,问最大覆盖长度;
题解:
正解\(DP\);
设定一神仙状态\(F[i][j]\),表示讨论到第\(i\)个点,限制区间覆盖必须在离散化后的\(j\)坐标之前;
分两种情况转移:
1.若\(j\)小于\(p_i\)的位置,那么显然为了做出贡献,\(p_i\)会选择向左喷:
\(F[i][j]=max\{F[i-1][l_i]+pos[j]-pos[l_i]\}\),如图:
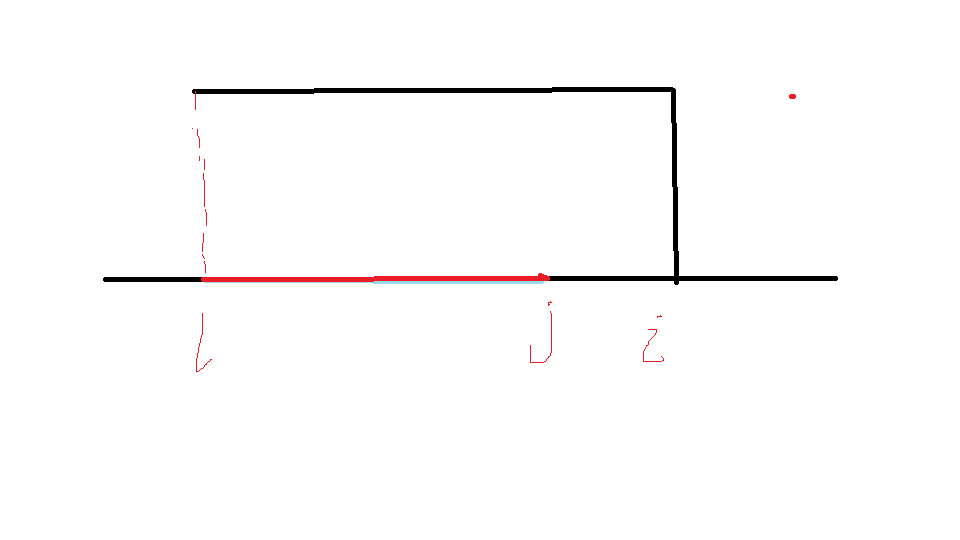
红色线段就是\(pos[j]-pos[l_i]\);
2.若\(j\)大于\(p_i\)的位置,那么\(p_i\)会选择向右喷;
同理可得:
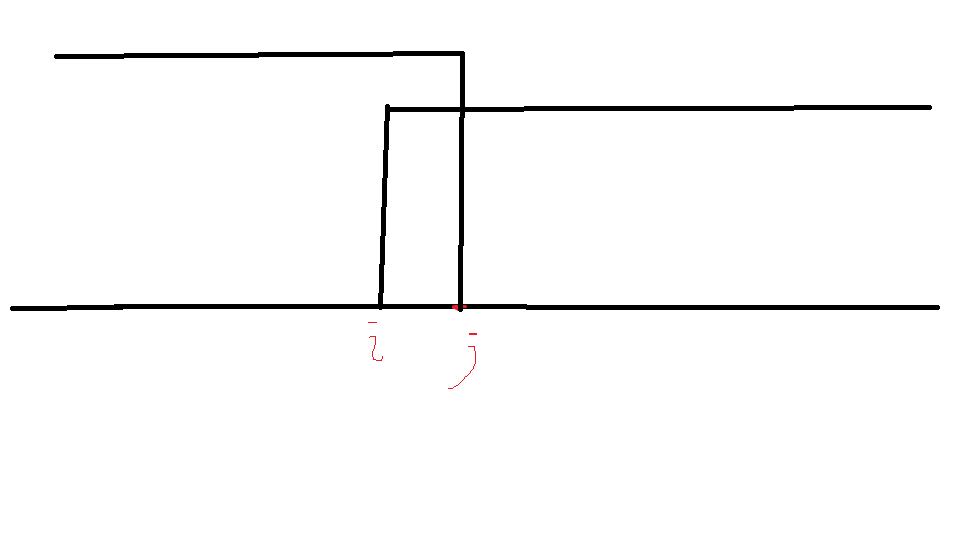
\(code:\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>
#include<ctype.h>
#include<vector>
#include<queue>
#define ld double
#define ls p<<1
#define rs p<<1|1
#define mid (l+r>>1)
#define ll long long
using namespace std;
char buf[1<<20],*p1,*p2;
inline char gc()
{
// return getchar();
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin))==p1?0:*p1++;
}
template<typename T>
inline void read(T &x)
{
char tt;
bool flag=0;
while(!isdigit(tt=gc())&&(tt!='-'));
tt=='-'?(flag=1,x=0):(x=(tt^'0'));
while(isdigit(tt=gc())) x=(x<<1)+(x<<3)+(tt^'0');
if(flag) x=-x;
}
const int maxn=3002;
struct node{
ll p,l,r;
inline node(ll a=0,ll b=0,ll c=0)
{p=a,l=b,r=c;}
inline bool operator<(node a)const
{return p<a.p;}
}a[maxn];
int n,tot;
int id[maxn*3];
ll hashh[maxn*3],f[2][maxn*3];
int main()
{
read(n);
for(int i=1;i<=n;i++)
{
ll x,y,z;
read(x),read(y),read(z);
a[i]=node(x,y,z);
hashh[++tot]=x;
hashh[++tot]=x-y;
hashh[++tot]=x+z;
}
sort(hashh+1,hashh+1+tot);
int m=unique(hashh+1,hashh+1+tot)-hashh-1;
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
{
a[i].l=lower_bound(hashh+1,hashh+1+m,a[i].p-a[i].l)-hashh;
a[i].r=lower_bound(hashh+1,hashh+1+m,a[i].p+a[i].r)-hashh;
a[i].p=lower_bound(hashh+1,hashh+1+m,a[i].p)-hashh;
if(!id[a[i].p] or a[id[a[i].p]].l>a[i].l) id[a[i].p]=i;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
f[i&1][j]=f[(i-1)&1][j];
for(int j=a[i].l+1;j<=a[i].p;j++)
f[i&1][j]=max(f[i&1][j],f[(i-1)&1][a[i].l]+hashh[j]-hashh[a[i].l]);
ll mx=f[(i-1)&1][a[i].p];
for(int j=a[i].p+1;j<=a[i].r;j++)
{
f[i&1][j]=max(f[i&1][j],mx+hashh[j]-hashh[a[i].p]);
if(id[j] and a[id[j]].l<a[i].p)
mx=max(mx,f[(i-1)&1][a[id[j]].l]+hashh[a[i].p]-hashh[a[id[j]].l]);
}
for(int j=1;j<=m;j++)
f[i&1][j]=max(f[i&1][j-1],f[i&1][j]);
}
// for(int i=1;i<=n;i++)
// printf("%d ",f[i][3]);
printf("%lld",f[n&1][m]);
}


