SNN_文献阅读_Effective and Efficient Computation with Multiple-timescaleSpiking Recurrent Neural Networks
Adaptive SRNN
基于多时间尺度脉冲循环神经网络的高效计算(SRNN)
中心思想:
使用替代梯度进行训练,克服SNN中梯度不连续的问题。
在PyTorch中直接使用BPTT进行训练。
结构
本文讨论由一个或者多个递归层组成的SNN——SRNN。
使用LIF神经元+Adaptive脉冲神经元
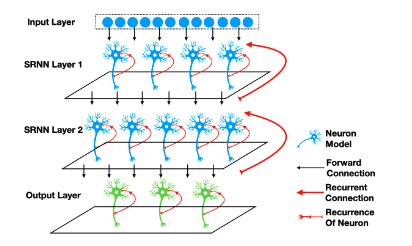
「具有两个循环层的SNN,循环层内神经元完全循环连接,层与层之间的神经元完全前向连接。」
基本组成
LIF神经元:
\(\hat{f_s}(u_t,\theta)\),其中\(u_t\)为膜电位,\(\theta\)为阈值。
对应公式:
\(\tau_{m} \frac{d u}{d t}=-\left(u_{t}-u_{r}\right)+R_{m} I_{t}\)
\(s_{t}=\hat{f}_{s}\left(u_{t}, \theta\right)\)
\(u_{t}=u_{t}\left(1-s_{t}\right)+u_{r} s_{t}\)
其中,\(I_t=\sum_{t_i}\delta (t_i)\)为输入,表示为脉冲串\(\{t_i\}\),\(u_t\)是按照时间常数\(\tau_m\)随指数衰减的膜电位,\(R_m\)是膜电阻,脉冲发射是阈值和电位的非线性函数\(S_{pike}=\hat{f}_{s}(u_{t})\)。
Adaptive脉冲神经元:
每次放电后阈值都会增加,随着时间常数\(\tau_{adp}\)指数衰减。用前向欧拉一阶指数积分器的方法在\(dt=1ms\)的离散时间内模拟连续神经元模型:
\(\alpha=\exp \left(-d t / \tau_{m}\right)\)
\(\rho=\exp \left(-d t / \tau_{a d p}\right)\)
\(\eta_{t}=\rho \eta_{t-1}+(1-\rho) S_{t-1}\)
\(\theta=b_{0}+\beta \eta_{t}\)
\(u_{t}=\alpha u_{t-1}+(1-\alpha) R_{m} I_{t}-S_{t-1} \theta\) &
\(\theta\)为动态阈值,\(\rho\)表示单时间步衰减。
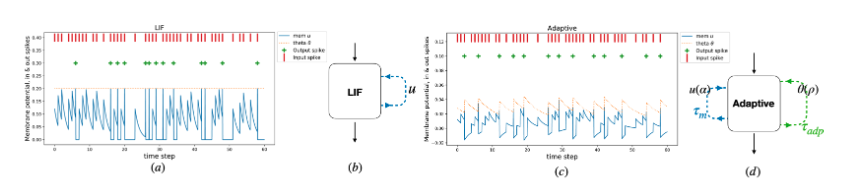
为了确定SNN的有效性,可以将SNN转换为具有ReLU激活功能的RNN网络,即在每个时间步将膜电位而不是偶尔的脉冲信号传递给其他的神经元,即将&替换为:
\(S_t=ReLU(u_t-\theta)\)
(即RELU SRNN)
BPTT:时间反向传播算法
用于训练SRNN。将输出预测值和输出目标之间的差值从输出传递回输入,包括过去的输入,通过梯度下降来优化权重和更新参数。
应用了交替梯度算法:通过放电神经元的不连续脉冲产生器来逼近误差梯度,替代梯度方法用一个将输出脉冲与膜电位联系起来的导数来代替不存在的梯度。
利用高斯分布:\(\hat{f}_{s}^{\prime}\left(u_{t}\right)=\mathcal{N}\left(u_{t} \mid \theta, \sigma^{2}\right)\)
其期望为阈值\(\theta\),方差为0.5,用来表示误差反向传播的膜电位值。
定义BPTT算法的损失函数并最小化损失函数,需要考虑不同任务下的标签类型:对于顺序分类任务,在序列末尾作为误差;对于时间流任务,在每一个时间步长生成一个输出并对其作为误差。
解码SRNN:解码SRNN的输出是对脉冲神经元行为的解释。输出神经元的膜电位和脉冲历史,频率编码或者到达时间编码都可以代表每一类神经元的信念。本文定义了一些输出编码方法和相关的损失函数。
基于脉冲的分类:
神经元发出脉冲的原因是膜电位到达了阈值。
分类任务中,最简单的方法就是统计某一段时间窗口内的脉冲数目,虽然简单但容易出错:(1)一些输出神经元可能发出相同数目的脉冲(2)神经元的重置和重现机制可能会降低强刺激脉冲的放电率(3)单个神经元的实时读出是不可行的。
因此,我们使用在每个时间步可用的输出神经元直接进行测量。
直接测量:输出神经元的膜电位可以用于分类,因为其代表了输出神经元的历史测量值。
定义了几种从膜电势历史中进行解码结果的方法:(1)最后时间步长的膜电势,即取样本最后一个时间步长的输出膜电位值作为输出。(2)最大的随时间变化的膜电位为:在呈现样本期间达到的最大膜电位作为输出神经元的值。(3)读出积分器:虽然膜电位可以被解释为神经元激活的移动平均,但脉冲引起的集合不符合这一概念。因此我们定义了一个非脉冲读出层,那里的膜电位是在没有神经元脉冲和重置的情况下计算的,这避免了脉冲神经元的重置机制对分类性能的影响。读出积分器被定义为:\(u_{t}=\alpha u_{t}+(1-\alpha) x_{t}\),其中\(u_t\)是输出膜电势,\(x_t\)是输入脉冲串,\(\alpha =e^{-\frac{\tau_m}{dt}}\),其中\(\tau_m\)是不可训练的时间常数,我们对非脉冲读出神经元使用随时间变化的平均值。
在【The Heidelberg spiking datasets for the systematic evaluation ofspiking neural networks】中使用了所有三种方法的变体,即对于流任务,每个时间步都需要分类,并且当只使用单个神经元来表示输出的时候,只能直接测量。为了训练网络,应用数据集8的时候使用交叉熵函数作为误差函数。在流任务中,读出膜电势被用作输出,在每个时间步与对应的目标进行比较。在分类任务中,将读取整个序列后的输出序列与正确标签进行比较。
我们在PyTorch中实现了各种SRNN,其中代理梯度的使用允许我们应用BPTT来有效地最小化损失,并利用标准的深度学习优化,包括对脉冲神经元参数的训练。
实验过程
QTDP、S-MNIST、PS-MNIST、SHD
编码和解码:
编码:DVS传感器转化 或者 基于速率的泊松时间编码。
解码:针对不同任务采用不同解码方式,QTDP任务采用膜电位直接解码方法;MNIST任务采用脉冲计数解码方法;SHD任务采用读出积分器方法。
能效
一个争议的问题为,SNN与ANN相比,是否能实现平均功率的降低。在这里,我们根据寄存器传输逻辑(RTL)级别的功率数从中推导出45nm CMOS工艺的理论能量值。
我们通过计算每个时间步所需的运算量来计算循环网络的理论能耗。我们计算了乘法和累加运算和累加运算。标准的人工神经元对每个输入都需要乘法和加法运算;相反,脉冲神经元只要求每个输入脉冲的累加运算,而它的内部状态动力学需要一些乘法和加法运算。
因此,在网络中,我们需要考虑神经元输入连接的数量、层中神经元的数量以及内部计算的成本。例如,考虑第l层的循环层,定义为:\(y_{l, t}=f\left(W \cdot x_{t}+W_{r e c} \cdot y_{l, t-1}\right)+b\),输入大小为m层,输出大小为n层:这需要两次乘法运算和一次累加运算。对于每一个时间步长,RNN所需要的能量计算为: \(Energy_{r n n}=(m n+n n) E_{MAC}\)。在SNN中,需要考虑稀疏脉冲活动(平均激发速率为\(F_r\)): \(Energy_{s r n n}=(m n+n n) E_{A C} F r\),且在稀疏脉冲的SRNN中, \(F r<<1\)。
我们计算了RNN的所有层l和所有时间步T的理论能量成本总和,\(E_{rnn}=\displaystyle\sum_{t\in T}\displaystyle\sum_{l\in L}Energy_{l,t}\):我们计算了表格2中的各种循环网络MACS/AC的能量消耗。
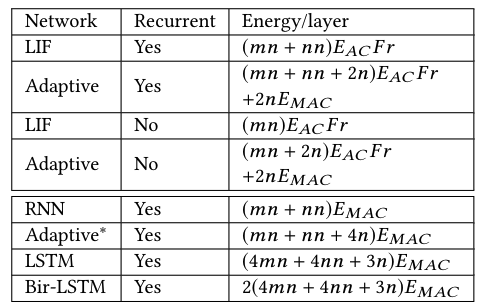
表格2:不同神经元的每层能量消耗。网络层的输入大小是m,输出大小是n。\(E_{AC}\)是每次累加运算的能量成本,\(E_{MAC}\)是每次长发和加法运算的成本。Adaptative*是非脉冲自适应神经元。
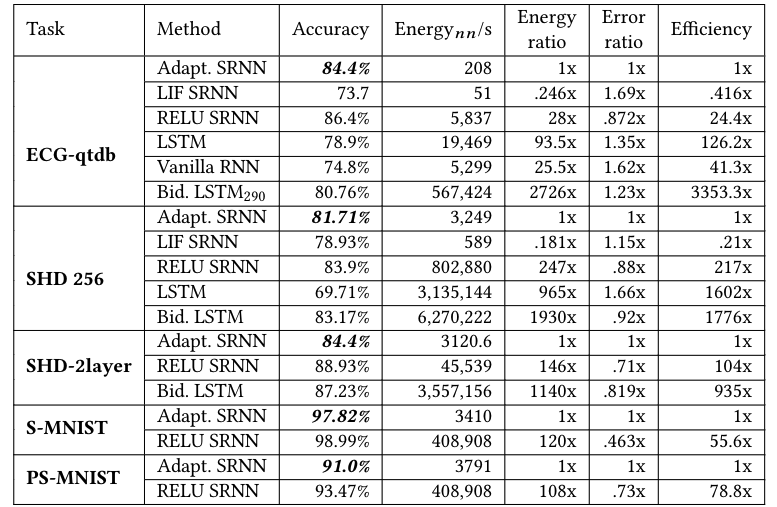
表格3:模型性能和能耗,实际相对能量成本。为了进行比较,将Adaptive SRNN的能耗和错误率设置为1倍。能量(energy)/误差(error)比被计算为能量(energy)/误差(error)相对于自适应SRNN的比率。效率定义为能量(energy)和错误率(error retio)的乘积。对于能耗测量\(E_{MAC}\)和\(E_{AC}\),使用[28]:一个32位MAC需要3.2pJ,一个32位AC需要0.1pJ。
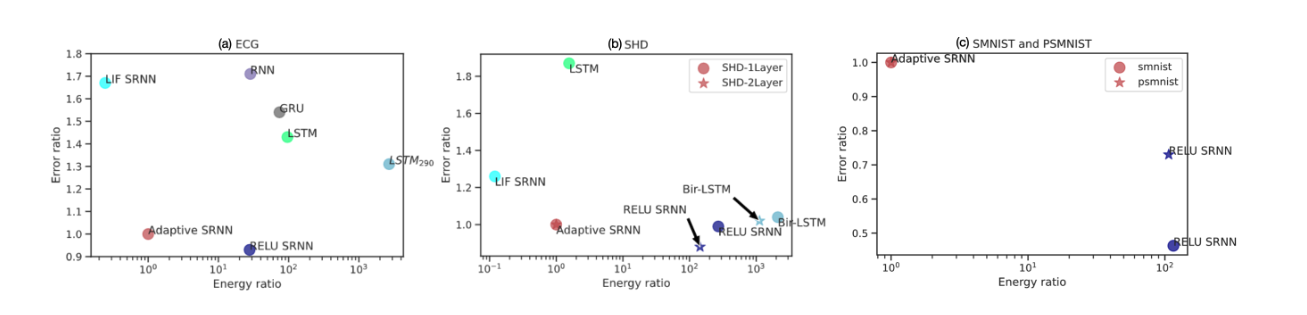
图8:各种网络精确度与能量比。SRNN的解决方案位于节能和高效网络的Pareto front,Adaptive SRNN获得了接近RELU SRNN的性能,但理论上的能源效率高出28-243倍。与更复杂的SHD和PSMNIST任务相比,我们计算出SRNN的能量效率高出100倍以上,因为在更大的网络中,输入端数量和稀疏性都增加了。



