CodeForces 786B Legacy

题意

有 \(n\) 个点和 \(q\) 次操作，每一次操作为以下三种类型中的一种 ：

• 1 u v w：连一条 \(u\to v\) 的单向边，权值为 \(w\)。

• 2 u l r w：对于所有 \(i\in [l,r]\) 连一条 \(u\to i\) 的单向边，权值为 \(w\)。

• 3 u l r w：对于所有 \(i\in [l,r]\) 连一条 \(i\to u\) 的单向边，权值为 \(w\)。

最后你需要求出点 \(s\) 到其他点的最短路。

\(\texttt{Data Range:}1\leq n,q\leq 10^5,1\leq w\leq 10^9\)

题解

好久没看线段树优化连边了，这次写篇题解来复习复习。

注意到如果 \(2\) 和 \(3\) 操作暴力搞的话那边数会爆炸，所以我们需要考虑将一个区间内的点缩成一个，于是自然想到用线段树来优化。

首先考虑只有 \(2\) 操作时怎么做。

考虑先建出线段树，对于某一个 \(u\) 向 \([l,r]\) 连边的操作，在线段树上搞出 \([l,r]\) 所对应的若干区间，然后 \(u\) 依次向这些区间连边即可。

但是这样是错的，因为一个线段树上代表的区间与子区间没有边连接所以跑最短路会出问题。所以在建树的时候，应该从这个区间向两个子区间连边权为 \(0\) 的边才行。

接下来考虑 \(3\) 操作，同样的思路，其实就是 \([l,r]\) 对应的若干区间向 \(u\) 连边，然后线段树中两个子区间向这个区间连边即可。

最后考虑 \(1\) 操作，由于线段树上的叶节点就是一个一个的单点，所以我们可以直接拿叶子节点互相连边即可。

这里有一个处理方法就是使用动态开点线段树，叶节点编号为 \(1\sim n\)，线段树上的非叶节点一个一个编号。也就是建两棵线段树，一棵代表往子区间连边，另一棵往父节点连边，其中叶节点是重合的，如图所示：

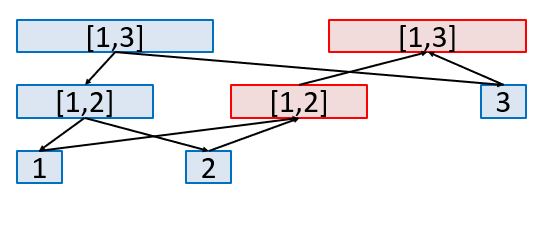
蓝色的节点代表从上往下连的，红色的代表从下往上连的，叶节点为两棵树所共享。

最后的最后，有一个实现细节，就是你写结构体式线段树会让你 T 到怀疑人生。

代码

#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
using namespace std;
typedef int ll;
typedef long long int li;
const ll MAXN=1e5+51;
const li inf=0x3f3f3f3f3f3f3f3f;
struct Edge{
    ll to,prev,dist;
};
struct Tuple{
    li x,y;
    inline bool operator <(const Tuple &rhs)const
    {
        return this->x>rhs.x;
    }
};
Edge ed[MAXN*20];
priority_queue<Tuple>pq;
ll cnt,nc,tot,rt,rtx,qcnt,source,op,x,y,l,r,dist;
ll last[MAXN<<2],inQueue[MAXN<<2],ls[MAXN<<2],rs[MAXN<<2];
li dis[MAXN<<2];
inline ll read()
{
    register ll num=0,neg=1;
    register char ch=getchar();
    while(!isdigit(ch)&&ch!='-')
    {
        ch=getchar();
    }
    if(ch=='-')
    {
        neg=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        num=(num<<3)+(num<<1)+(ch-'0');
        ch=getchar();
    }
    return num*neg;
}
inline void addEdge(ll from,ll to,ll dist)
{
    ed[++tot].prev=last[from];
    ed[tot].to=to;
    ed[tot].dist=dist;
    last[from]=tot;
}
inline ll createDown(ll l,ll r)
{
    if(l==r)
    {
        return l;
    }
    ll mid=(l+r)>>1,cur=++nc;
    ls[cur]=createDown(l,mid),rs[cur]=createDown(mid+1,r);
    addEdge(cur,ls[cur],0),addEdge(cur,rs[cur],0);
    return cur;
}
inline ll createUp(ll l,ll r)
{
    if(l==r)
    {
        return l;
    }
    ll mid=(l+r)>>1,cur=++nc;
    ls[cur]=createUp(l,mid),rs[cur]=createUp(mid+1,r);
    addEdge(ls[cur],cur,0),addEdge(rs[cur],cur,0);
    return cur;
}
ll lx,rx;
inline void link(ll l,ll r,ll x,ll dist,ll node,ll type)
{
    if(lx<=l&&rx>=r)
    {
        type?addEdge(node,x,dist):addEdge(x,node,dist);
        return;
    }
    ll mid=(l+r)>>1;
    if(lx<=mid)
    {
        link(l,mid,x,dist,ls[node],type);
    }
    if(rx>mid)
    {
        link(mid+1,r,x,dist,rs[node],type);
    }
}
inline void Dijkstra(ll source)
{
    ll top;
    dis[source]=0,inQueue[source]=1,pq.push((Tuple){0,source});
    while(!pq.empty())
    {
        top=pq.top().y,pq.pop(),inQueue[top]=0;
        for(register int i=last[top];i;i=ed[i].prev)
        {
            if(dis[ed[i].to]>dis[top]+ed[i].dist)
            {
                dis[ed[i].to]=dis[top]+ed[i].dist;
                if(!inQueue[ed[i].to])
                {
                    inQueue[ed[i].to]=1;
                    pq.push((Tuple){dis[ed[i].to],ed[i].to});
                }
            }
        }
    }
} 
int main()
{
    cnt=nc=read(),qcnt=read(),source=read();
    rt=nc+1,createDown(1,cnt),rtx=nc+1,createUp(1,cnt);
    for(register int i=0;i<qcnt;i++)
    {
        op=read();
        if(op==1)
        {
            x=read(),y=read(),dist=read(),addEdge(x,y,dist);
            continue;
        }
        x=read(),lx=read(),rx=read(),dist=read();
        link(1,cnt,x,dist,op^3?rt:rtx,op-2);
    }
    memset(dis,0x3f,sizeof(dis)),Dijkstra(source);
    for(register int i=1;i<=cnt;i++)
    {
        printf("%lld ",dis[i]==inf?-1:dis[i]);
    }
}