三维坐标转二维坐标

最近在帮朋友调代码，他们想出份报告，需要把三维的坐标系以一定的角度画到纸面上。

公式：x =  x'Cosα + z'Cosβ     y = y' - z'Sinβ + x'Cosα

以下是公式推导过程

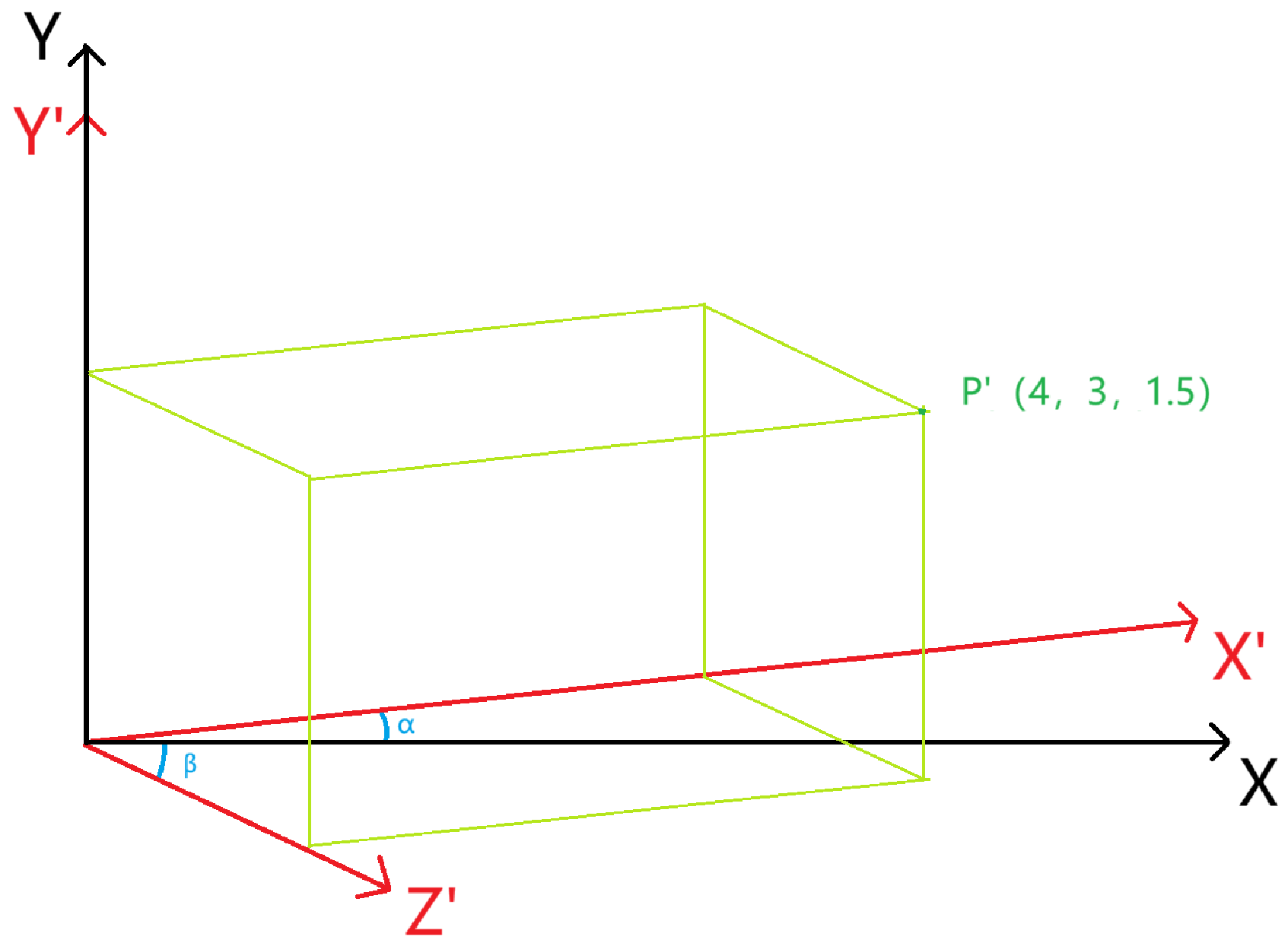
1. 先画平面直角坐标系(xy坐标系)和空间直角坐标系(xyz坐标系，本文用x'，y'，z'表示)，x轴和x'轴之间的夹角为α，x轴和z'轴之间的夹角为β，三维点P'(4, 3, 1.5)，如图所示。我们要计算的就是P点对应的二维坐标。

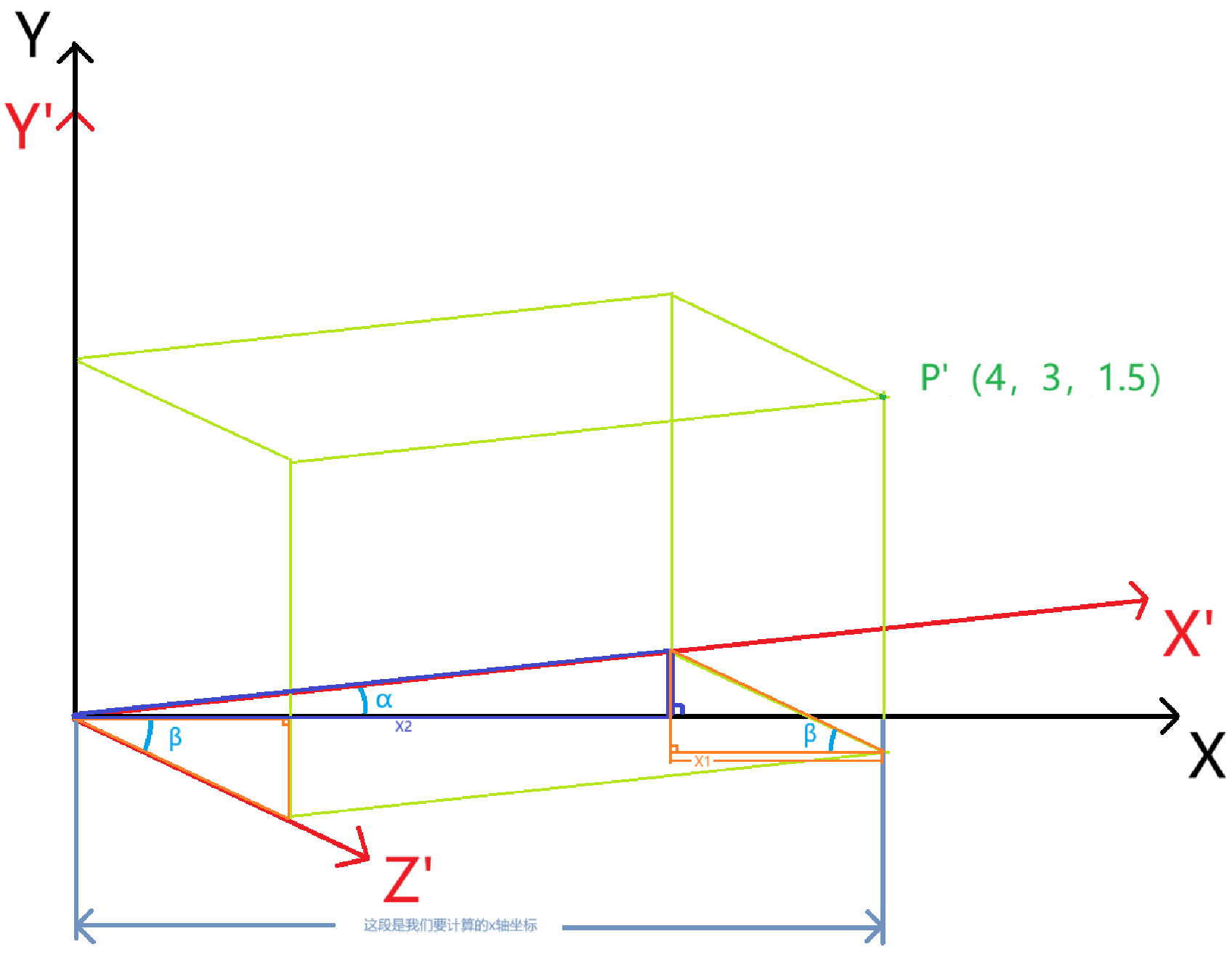
2.  从点(4, 0, 0) 做垂直X轴垂直线，可以得到深蓝色的直角三角形，直角三角形的其中一个角度是α，α的斜边为4（p' 点x' 轴坐标），α的邻边x2 = x'Cosα。

再从点(0, 0, 1.5)做垂直X轴垂直线， 可以得到橙色的直角三角形（图中两个橙色三角形互为全等三角形），直角三角形的其中一个角度是β，β的斜边为1.5（p'点z'轴坐标），β的邻边x1 = z'Cosβ。

所以我们可以得到公式：x = x1 + x2 = x'Cosα + z'Cosβ。

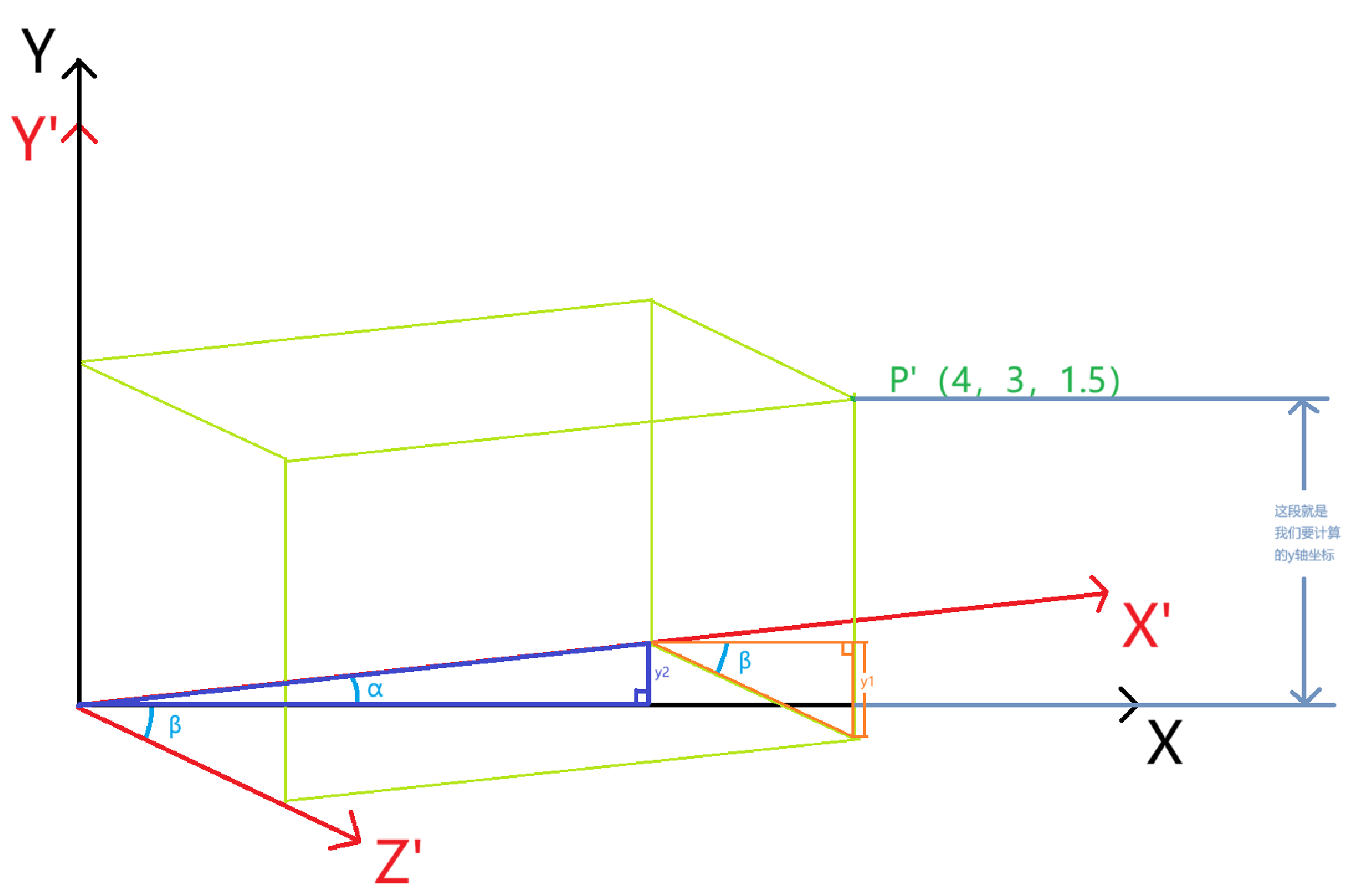
3. 从点(4, 0, 0)做垂直X轴垂直线，可以得到深蓝色的直角三角形，直角三角形的其中一个角度是α，α的斜边为4（p'点x'轴坐标），α的对边y2 = x'Cosα。

再从点(4, 0, 0)做垂直Y轴垂直线， 可以得到橙色的直角三角形，直角三角形的其中一个角度是β，β的斜边为1.5（p'点z'轴坐标），β的对边y1 = z'Sinβ。

所以我们可以得到公式：y = y' - y1 + y2 = y' - z'Sinβ + x'Cosα。

 最后，三维坐标转换成二维坐标，是一种降维度操作，也称为投影。就是把三维图像以一定的角度投影出来，投影的角度不同，推导公式不同，但推导的方法是一样的。