Codeforces Round #671 (Div. 2)

比赛链接：https://codeforces.com/contest/1419

A. Digit Game

题意

给出一个 $n$ 位数，游戏规则如下：

1-indexed
Raze标记奇数位
Breach标记偶数位
如果最后剩下的一位未标记位上的数字为奇数，Raze胜，为偶数，Breach胜

问Raze先手能否胜利。

题解

根据 $n$ 的奇偶性可得最后的未标记位的奇偶性，然后判断该奇偶性的位置上是否存在奇数或偶数即可。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        string s;
        cin >> s;
        bool Raze = true;
        if (s.size() & 1) {
            Raze = false;
            for (int i = 0; i < int(s.size()); i += 2) {
                if ((s[i] - '0') & 1)
                    Raze = true;
            }
        } else {
            Raze = true;
            for (int i = 1; i < int(s.size()); i += 2) {
                if ((s[i] - '0') % 2 == 0)
                    Raze = false;
            }
        }
        cout << (Raze ? 1 : 2) << "\n";
    }
    return 0;
}

B. Stairs

题意

共有 $n$ 个边长为 $1$ 的小正方形可用，问能拼成多少个不同的可以被完美覆盖的阶梯。

边长为1、3、7的阶梯都可以被完美覆盖，方式如下：

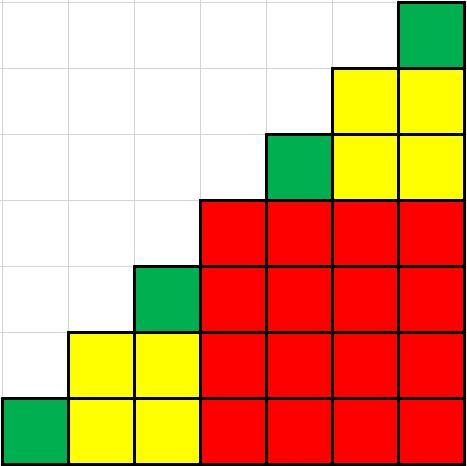
题解

完美阶梯的边长是以 $2$ 的幂次递增的，当前阶梯所用小正方形块数 = 上一个所用块数 X 2 + 递增步长²。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        long long x;
        cin >> x;
        int ans = 0;
        long long pre = 0, now = 0;
        for (long long i = 1; true; i *= 2) {
            now = 2 * pre + i * i;
            x -= now;
            pre = now;
            if (x >= 0) {
                ++ans;
            } else {
                cout << ans << "\n";
                break;
            }
        }
    }
    return 0;
}

C. Killjoy

题意

有一个初始时感染的账号，Rating为 $x$，感染规则如下：

Rating相同的账号相互感染
可以举办比赛任意加减Rating，但应保证总的变化之和为零，即比赛前后总Rating和不变
初始账号不能参加比赛

给出 $n$ 个账号的Rating，计算感染完所有账号至少要举办多少场比赛。

题解

如果总Rating之和为 $x$ 的倍数：

如果均为 $x$，无需举办
否则举办一场将总Rating均分即可

如果总Rating之和不为 $x$ 的倍数：

如果有 $x$，感染 $x$ 后举办一场比赛将其他账号都变为 $x$
否则需要先举办一场得到一个 $x$，之后同上

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        int n, x;
        cin >> n >> x;
        vector<int> a(n);
        int sum = 0;
        for (int i = 0; i < n; i++) {
            cin >> a[i];
            sum += a[i];
        }
        if (sum % n == 0 and sum / n == x) {
            if (all_of(a.begin(), a.end(), [&](int y) { return y == x; }))
                cout << 0 << "\n";
            else
                cout << 1 << "\n";        
        } else {
            if (any_of(a.begin(), a.end(), [&](int y) { return y == x; }))
                cout << 1 << "\n";
            else
                cout << 2 << "\n";
        }
    }
    return 0;
}

D2. Sage's Birthday (hard version)

题意

给出 $n$ 个数，试重新排列使得相邻两个数比自己大的数的个数最多。

题解一

先将较小的一半放在中间，然后upper_bound查找每个数左边相邻的数，剩下的数依次填补空位即可。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    sort(a.begin(), a.end());
    multiset<int> st(a.begin(), a.end());
    vector<int> v(n);
    for (int i = 1, j = 0; i < n; i += 2) {
        v[i] = a[j];
        st.erase(st.find(a[j]));
        ++j;
    }
    for (int i = 1; i < n; i += 2) {
        auto it = st.upper_bound(v[i]);
        if (it != st.end()) {
            v[i - 1] = *it;
            st.erase(it);
        }
    }
    for (int i = 0; i < n; i++) {
        if (v[i] == 0) {
            v[i] = *st.begin();
            st.erase(st.begin());
        }
    }
    int ans = 0;
    for (int i = 1; i + 1 < n; i += 2) {
        if (v[i - 1] > v[i] and v[i + 1] > v[i]) 
            ++ans;
    }
    cout << ans << "\n";
    for (auto i : v) cout << i << ' ';
    return 0;
}

题解二

先将较小的一半放在中间，然后将较大的一半放在两边。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    sort(a.begin(), a.end());
    vector<int> v(n);
    int cur = 0;
    for (int i = 1; i < n; i += 2) {
        v[i] = a[cur++];
    }
    for (int i = 0; i < n; i += 2) {
        v[i] = a[cur++];
    }
    int ans = 0;
    for (int i = 1; i + 1 < n; i += 2) {
        if (v[i - 1] > v[i] and v[i] < v[i + 1])
            ++ans;
    }
    cout << ans << "\n";
    for (auto i : v) cout << i << ' ';
    return 0;
}

E. Decryption

题意

将一个合数所有大于 $1$ 的因子围成一个环，使得相邻互质的数最少。

题解

质因子分解和DFS，将DFS过程中最高位不为 $0$ 的质因子作为 $gcd$ 分组。

例如：

$30 = 2^1 \times 3^1 \times 5^1$

DFS过程如下:

一组（$gcd = 5$）：

$5 = 2^0 \times 3^0 \times 5^1$

二组（$gcd = 3$）：

$3 = 2^0 \times 3^1 \times 5^0$

$15 = 2^0 \times 3^1 \times 5^1$

三组（$gcd = 2$）：

$2 = 2^1 \times 3^0 \times 5^0$

$10 = 2^1 \times 3^0 \times 5^1$

$6 = 2^1 \times 3^1 \times 5^0$

$30 = 2^1 \times 3^1 \times 5^1$

发现不同组之间首尾互质（当然了），可以根据DFS的性质：后一组的最大数一定会覆盖前一组的任意一个数将每组反转，得到：

15 3

30 6 10 2

此时只有 $5$ 和 $2$ 互质，再根据DFS的性质将最后一组末尾两个数交换，最终得到：

5 15 3 30 6 2 10

此时也可以发现相邻互质的数的对数最少为 $0$ 或 $1$，之后模拟上述过程即可。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        //质因子分解
        vector<int> p, e;
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                p.push_back(i);
                e.push_back(0);
                while (n % i == 0) {
                    ++e.back();
                    n /= i;
                }
            }
        }
        if (n > 1) {
            p.push_back(n);
            e.push_back(1);
        }
        //num低位至高位代表从小到大的质因子
        vector<int> num(100);
        function<int(void)> cal_num = [&]() {
            int res = 1;
            for (int i = 0; i < int(p.size()); i++) {
                int mul = 1;
                for (int j = 0; j < num[i]; j++) {
                    mul *= p[i];
                }
                res *= mul;
            }
            return res;
        };
        //对质因子的指数进行dfs
        map<int, vector<int>> mp;
        vector<int> order;
        function<void(int, int)> dfs = [&](int dep, int top_dep) {
            if (dep == int(p.size())) {
                int x = cal_num();
                if (x > 1) {
                    if (int(order.size()) == 0 or top_dep != order.back()) {
                        order.push_back(top_dep);
                    }
                    mp[order.back()].push_back(x);
                }
                return;
            }
            for (int i = 0; i <= e[dep]; i++) {
                num[dep] = i;
                if (i >= 1 and top_dep == -1)
                    dfs(dep + 1, dep);
                else
                    dfs(dep + 1, top_dep);
            }
        };
        dfs(0, -1);
        //反转每组因子
        vector<int> ans;
        for (int i = 0; i < int(order.size()); i++) {
            reverse(mp[order[i]].begin(), mp[order[i]].end());
            for (auto j : mp[order[i]]) ans.push_back(j);
        }
        //交换最后一组的后两个元素
        swap(ans.back(), ans[int(ans.size()) - 2]);
        for (int i = 0; i < int(ans.size()); i++) {
            cout << ans[i] << " \n"[i == int(ans.size()) - 1];
        }
        //最多有一对因子互质，即只有两个素因子的情况，也可以逐对判断
        cout << (__gcd(ans[0], ans[1]) == 1) << "\n";
    }
    return 0;
}

posted @ 2020-09-21 23:00 Kanoon 阅读(228) 评论(0) 编辑收藏举报

刷新页面返回顶部

Kanoon