Codeforces Round #652 (Div. 2) D. TediousLee(dp)
题目链接:https://codeforces.com/contest/1369/problem/D
题意
最初有一个结点,衍生规则如下:
- 如果结点 $u$ 没有子结点,添加 $1$ 个子结点
- 如果结点 $u$ 有 $1$ 个子结点,添加 $2$ 个子结点
- 如果结点 $u$ 有 $3$ 个子结点,跳过该结点
如:
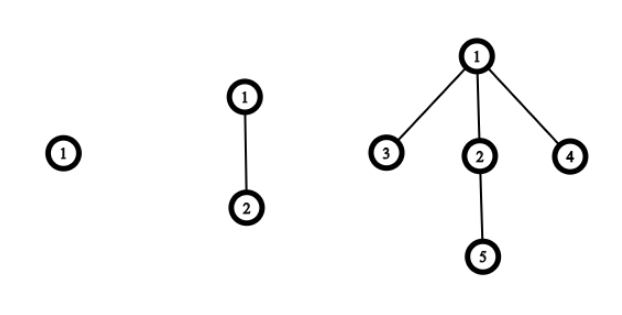
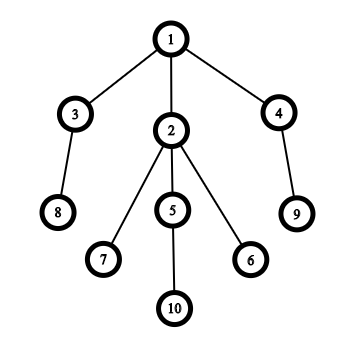
\begin{equation} level = 1, 2, 3,4 \end{equation}
爪形结构如下:
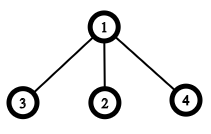
问可以在 $level_n$ 选出几个互不相交的爪形结构。
题解
衍生的过程是具有重复性的,最终变化的是根结点 $1$ 下的三棵子树,左右两棵子树为 $level_{n - 2}$,中间的子树为 $level_{n - 1}$ 。
因为 $level_1$ 和 $level_2$ 的根结点并未使用,所以可以在 $level_3$ 中选择以根结点 $1$ 为中心的爪形结构。
同理,$level_4$、$level_5$ 可以通过选取较下层的爪形结构来避免根结点的使用,所以在 $level_6$ 中又可以选取以根结点 $1$ 为中心的爪形结构。
即,$level$ 为 $3$ 的倍数的图形都可以再额外选取位于根结点的爪形结构。
综上,设 $dp_i$ 为 $level_i$ 中最多可选出的互不相交的爪形结构个数,有递推式:
\begin{equation} dp_i = 2 \times dp_{i - 2} + dp_{i - 1} + (i\ \%\ 3 == 0) \end{equation}
代码
#include <bits/stdc++.h> using namespace std; constexpr int N = 2e6 + 10; constexpr int mod = 1e9 + 7; int dp[N]; void init() { dp[1] = dp[2] = 0; dp[3] = dp[4] = 1; for (int i = 5; i < N; i++) dp[i] = (2LL * dp[i - 2] + dp[i - 1] + (i % 3 == 0)) % mod; } void solve() { int n; cin >> n; cout << 4LL * dp[n] % mod << "\n"; } int main() { init(); int t; cin >> t; while (t--) solve(); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号