Educational Codeforces Round 87 (Rated for Div. 2)

比赛链接：https://codeforces.com/contest/1354

A - Alarm Clock

题意

一个人要睡够 $a$ 分钟，一开始睡 $b$ 分钟后闹钟响铃，之后每次设置 $c$ 分钟后响铃，设置好后需要 $d$ 分钟入睡。

题解

首先判断能不能一开始就睡足 $a$ 分钟，如果不能判断能不能入睡，如果可以用需要补睡的时间对每次可以睡着的时间取上整。

代码

#include <bits/stdc++.h>
using ll = long long;
using namespace std;

void solve() {
    ll a, b, c, d; cin >> a >> b >> c >> d;
    if (b >= a) {
        cout << b << "\n";
    } else {
        ll need = a - b;
        if (c <= d)
            cout << -1 << "\n";
        else
            cout << b + c * ((need + c - d - 1) / (c - d)) << "\n";
    }
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

B - Ternary String

题意

字符串 $s$ 由 1,2,3 组成，输出包含 1,2,3 的最短连续子串。

题解

记录 1,2,3 的位置，枚举 1,2,3 的前后关系即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;

void solve() {
    string s; cin >> s;
    vector<int> pos[3];
    for (int i = 0; i < s.size(); i++) {
        pos[s[i] - '1'].push_back(i);
    }
    int p[3] = {0, 1, 2};
    int ans = INF;
    do {
        for (int a : pos[p[0]]) {
            auto b = upper_bound(pos[p[1]].begin(), pos[p[1]].end(), a);
            if (b == pos[p[1]].end()) break;
            auto c = upper_bound(pos[p[2]].begin(), pos[p[2]].end(), *b);
            if (c == pos[p[2]].end()) break;
            ans = min(ans, *c - a + 1);
        }
    } while(next_permutation(p, p + 3));
    cout << (ans == INF ? 0 : ans) << "\n";
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

C1 - Simple Polygon Embedding

题意

计算能包含正多边形的正方形的最小边长，正多边形可以旋转。（多边形的边数为 2 * 偶数）

题解

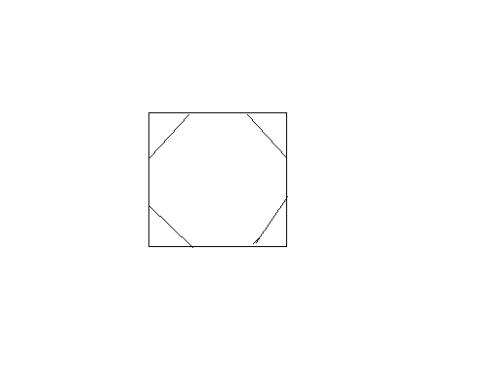
这是正八边形时的情况，观察发现边数为四的倍数的正多边形都可以恰好对称地四等分嵌在正方形中，所以计算出内切圆直径即可。

代码

#include <bits/stdc++.h>
#define PI acos(-1)
using namespace std;

void solve() {
    int n; cin >> n;
    n = 2 * n;
    printf("%.9f\n", cos(PI / n) / sin(PI/ n));
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

C2 - Not So Simple Polygon Embedding

题意

计算能包含正多边形的正方形的最小边长，正多边形可以旋转。（多边形的边数为 2 * 奇数）

题解

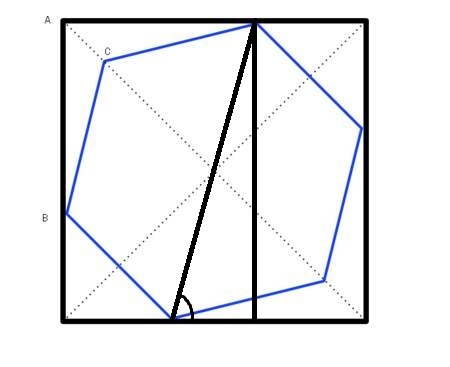
正六边形时大概长这样，算出正六边形与正方形的边较小的夹角为 15 度，求出对角线长乘以 sin 即可，其他边数情况我不太会证，但是觉得应该和正六边形差不多emmm...

代码

#include <bits/stdc++.h>
#define PI acos(-1)
using namespace std;

void solve() {
    int n; cin >> n;
    n = 2 * n;
    printf("%.9f\n", 0.5 / sin(PI / (2 * n)));
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

D - Multiset

题意

开始时 $multiset$ 中有 $n$ 个元素，之后 $q$ 次操作如下：

$k_i > 0$，插入 $k_i$
$k_i < 0$，删除第 $|k_i|$ 个元素（删除元素的序号不会大于集合的大小）

题解

树状数组模拟。

代码一

复杂度：$O_{(nlog_n)}$，参考自：square1001

#include <bits/stdc++.h>
using namespace std;
const int N = 1048576;

int bit[N];

void add(int pos, int val) {
    for (int i = pos; i <= N; i += i & (-i)) {
        bit[i] += val;
    }
}

int bsearch(int x) {
    int ptr = 0;
    for (int i = N / 2; i >= 1; i >>= 1) {
        if (bit[ptr + i] < x) {
            x -= bit[ptr + i];
            ptr += i;
        }
    }
    return ptr + 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, q; cin >> n >> q;
    for (int i = 0; i < n; i++) {
        int x; cin >> x;
        add(x, 1);
    }
    int cnt = n;
    for (int i = 0; i < q; i++) {
        int x; cin >> x;
        if (x > 0) {
            add(x, 1);
            ++cnt;
        } else {
            add(bsearch(-x), -1);
            --cnt;
        }
    }
    cout << (cnt ? bsearch(1) : 0);
}

代码二

复杂度：$O_{(nlog_n^2)}$，参考自：_封刀看海

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 100;

int bit[N];

void update(int pos, int val) {
    for (int i = pos; i <= N; i += i & (-i)) {
        bit[i] += val;
    }
}

int query(int pos) {
    int ans = 0;
    for (int i = pos; i >= 1; i -= i & (-i)) {
        ans += bit[i];
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, q; cin >> n >> q;
    for (int i = 0; i < n; i++) {
        int x; cin >> x;
        update(x, 1);
    }
    for (int i = 0; i < q; i++) {
        int x; cin >> x;
        if (x > 0) {
            update(x, 1);
        } else {
            int l = 1, r = N;
            while (l < r) {
                int mid = (l + r) / 2;
                if (query(mid) >= -x) 
                    r = mid;
                else 
                    l = mid + 1;
            }
            update(l, -1);
        }
    }
    int ans = find_if(bit, bit + N, [] (int x) {
        return x > 0;
    }) - bit;
    cout << (ans == N ? 0 : ans);
}

posted @ 2020-05-18 16:00 Kanoon 阅读(207) 评论(0) 编辑收藏举报

刷新页面返回顶部

Kanoon