3.4 Fundamentals of Spatial Filtering
本章介绍了空间滤波器的一些概念。
线性空间滤波器
线性空间滤波器在图像\(f\)和滤波核\(w\)之间进行运算。滤波核是一个数组,其大小定义了运算的区域,其系数决定了滤波器的性质。\(filter\ kernel\)可以称为mask,template,window。
一般来说,核大小都是奇数。进行滤波的一般公式如下:
其中,核大小为\(m\times n,m=2a+1,n=2b+1\)。在这个式子中,\(x\)和\(y\)是变化的,这样这个式子可以遍历到图像中的每个像素。若将\(x\)与\(y\)固定,则有:
为什么使用奇数大小:方便索引,并且滤波器是空间对称的。
空间相关与卷积
空间相关与卷积原理相同,区别在于,卷积将空间相关的滤波器旋转了\(180°\)。
一维
首先是一维卷积:
下面是一个例子:

可以看到,空间相关与卷积的差别只是将卷积核反转了\(180°\)。需要注意的是,因为起始是将图像的原点与卷积核的中心对准,所以左右必须进行\(0\)填充。
对上图的一些解释:
\(g(0)=w(-2)f(-2)+w(-1)f(-1)+\dots +w(2)f(2)=0\)相当于卷积核在图像上进行移动,相乘求和,最后的结果对应于输出图像的一个像素。
当内核\(w\)与只包含一个\(1\),其余为\(0\)的\(f\)相关联时,会将w水平反转180°(像上图一样)。这种只有一个\(1\),其余全为\(0\)的\(f\)称为离散单元脉冲。
上图右侧是卷积的相关操作,内核被事先旋转,所以最后我们得到的结果就是内核的准确复制。
二维
二维操作与一维类似。对于二维,将核旋转\(180°\)相当于在\(x\)和\(y\)轴上同时做对称。

脉冲是线性系统理论的基础。位于坐标\((x_0,y_0)\)的离散强度脉冲(振幅)A定义为:
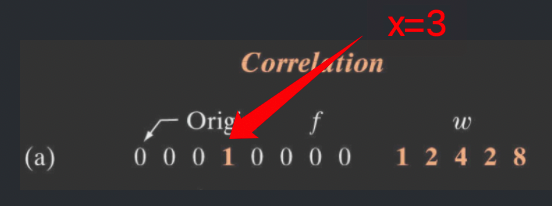
比如下图中,只有当x=3时有值。这就可以表示为\(\sigma(x-3)\)(而且在这个例子中,振幅A为1,所以这还是一个单元脉冲)
对上面的空间相关总结如下:
一张图片\(f(x,y)\),核\(w\),大小为\(m\times n\),空间相关的操作记为:
卷积相关的操作如下:
其中\(m,n\)为奇数,并且\(a=(m-1)/2,b=(n-1)/2\)。
下表是空间相关与卷积的相关性质:
| 性质 | 卷积 | 相关 |
|---|---|---|
| 对称性 | \(f★g=g★f\) | - |
| 结合律 | \(f★(g★h)=(f★g)★h\) | - |
| 分配律 | \(f★(g+h)=(f★g)+(f★h)\) | \(f☆(g+h)=(f☆g)+(f☆h)\) |
有时候,每个阶段会使用不同的内核,按顺序、分阶段对图像进行过滤(卷积):
注意,对于空间相关不适用于上面的式子,因为只有卷积具有交换律。
Separable Filter Kernels
一个二维函数G(x,y)如果可以写为两个一维函数的乘积,则称它是可分离的:
对于卷积核\(\omega\)来说,\(\omega\)可以分离为\(\omega=vw^T\)
结合上面的卷积结合律,一个输入\(f\)与卷积核\(\omega\)可以写为
也就是说,对一张图片进行卷积,可以通过将卷积核先分解为两个小卷积核\(w_1\)和\(w_2\),然后分别进行卷积。
对于一张大小为\(M\times N\)的图片和一个\(m\times n\) 大小的核,如果使用\((6)\)的方式计算,一共需要\(MNmn\)次加法与乘法。但是如果将核分离,并先计算\(w_1★f\),需要使用\(MNm\)次加法与乘法;将上一步的结果再与\(w_2\)进行卷积,需要\(MNn\)次。一共加起来是\(MN(m+n)\)次。与不分离相比,计算量的优势为:
由矩阵原理可知,一个列向量与行向量相乘,结果的秩总是1。所以说,一个可分离的核,其秩一定是1。
现在假设有一个秩为1的矩阵,用下面三步来将其分解为两个向量\(v\)和\(w\)的乘积:
- 现在矩阵中找到任何非零元素,并让E代表其值;
- 让向量\(c\)和\(r\)等于在步骤1中知道到的元素所在的行和列;
- 参考\(\omega=vw^T\),让\(v=c,w^T=r/E\)。
例如:\(kernel=\left[ \matrix{ 1&2&3\\4&5&6\\7&8&9 }\right]\),先任意找到一个非零元素E,比如2。然后用c表示其列向量,\(c=\left[ \matrix{2\\4\\6}\right]\),\(r\)表示其行向量,\(r=\left[\matrix{2&4&6}\right]\)。\(v=c=\left[ \matrix{2\\4\\6}\right],w=\frac{1}{E}r=\frac{1}{2}\left[\matrix{2&4&6}\right]=\left[\matrix{\frac{1}{2}&1&\frac{3}{2}}\right]\)
循环对称核(circularly symmetric kernels):可以使用核中心的一列来描述整个核,\(w=vv^T/c\),\(c\)为核中心的值。将这个核分解,可以得到\(w_1=v,w_2=v^T/c\)。


