2.6 Basic Mathematical Tools

线形运算的定义

若给定一张图片\(f(x,y)\)，则通过一系列变换得到\(g(x,y)\)

\[H[f(x,y)]=g(x,y) \]

若\(H\)为线形运算，则

\[\begin{align}H[af_1(x,y)+bf_2(x,y)]=&aH[f_1(x,y)]+bH[f_2(x,y)]\\=&ag_1(x,y)+bg_2(x,y)\end{align} \]

图像的加法运算

图像的加法运算表示为

\[s(x,y)=f(x,y)+g(x,y) \]

加法运算可以用来进行图像降噪。

定义\(g(x,y)\)是由两部分组成：

\[g(x,y)=f(x,y)+\eta(x,y) \]

其中\(f(x,y)\)是图像的无噪声版本，\(\eta(x,y)\)是图像的带噪声版本。

在这里，假设每一个像素点\((x,y)\)都是不相关的，并且噪声点的灰度平均值为0。

如果一张图片是由多个噪声图片的平均值构成的：

\[\bar{g}(x,y)=\frac{1}{K}\sum_{i=1}^{K}g_i(x,y) \]

然后

\[E\{\bar{g}(x,y)\}=f(x,y)\\ \sigma^{2}_{\bar{g}(x,y)}=\frac{1}{K}\sigma_{\eta(x,y)}^{2} \]

这里注意，因为上面限制了\(\eta(x,y)\)的平均值为0，所以在（7）中，求和然后做期望，\(\eta\)部分为0；而且因为是一张图片，所以\(f(x,y)\)只有一个。

标准差为

\[\sigma_{\bar{g}(x,y)}=\frac{1}{\sqrt{K}}\sigma_{\eta(x,y)} \]

（8）表明，当\(K\)增大时，标准差减小，也就意味着平均后的图片与无噪音的图片的差距减小。当\(K\)足够大时，可以视为图片无噪音。

如下图所示，图\(a\)为原图，经过了多次求和、平均之后，图片的细节更加突出。

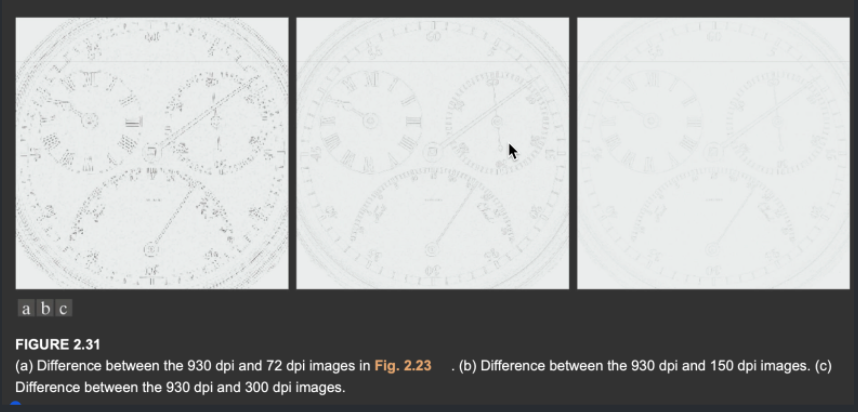
图像的减法运算

\[g(x,y)=f(x,y)-h(x,y) \]

图像的减法操作一般用来比较图像之间的差异。在医学领域，常用于血管造影。

图像的乘法（除法）运算

\[g(x,y)=f(x,y)h(x,y) \]

假如\(g(x,y)\)为传感器采集到的图像，由于光学折射的不均匀，图像在边缘可能有一些阴影。\(f(x,y)\)是图像的“完美状态”，\(h(x,y)\)是单一的背景。则\(f(x,y)\)可以由（10）得到。

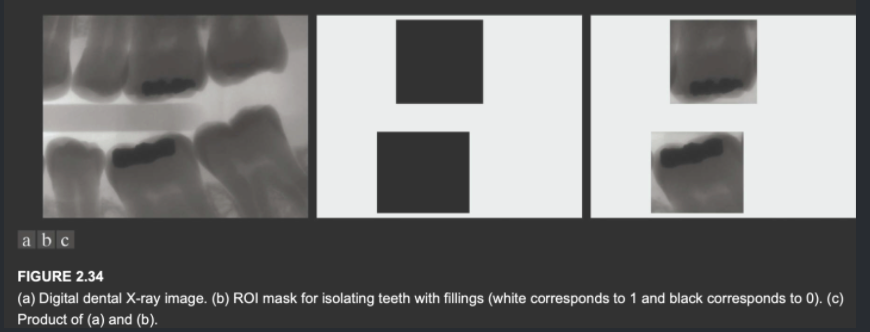
另一个应用是mask模板图像，也就是\(region of interest(ROI)\)。设置ROI区域为1，其余位置为0，将图像与mask相乘，则得到了目标ROI。

大多数图像都使用8bits来表示（24位的彩色图像是由3个8位通道组成）。所以图像的灰度值一般为0~255。当图像相减时，值可能为负，则只需将负值设为0；相加时若超过255，则最大值限制为255.

集合与逻辑操作

在灰度图上的集合操作：

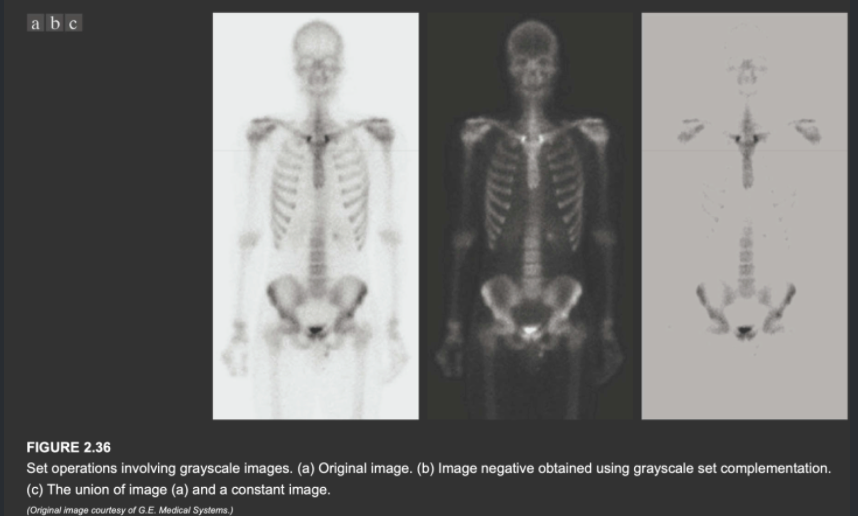
补集

用\((x,y,z)\)来表示一张图像，其中\(x,y\)为元素的坐标，\(z\)为图像的灰度值。定义图像的补集为

\[A^c=\{(x,y,K-z)\mid (x,y,z)\in{A}\} \]

集合中的点的灰度值是由图像的最大灰度值\(K=2^k-1\)减去每个点的灰度值组成的。若图像为\(8bits\)，则\(K=255\)。

交集

灰度图A与B的交集定义为

\[A\bigcup{B}=\{\mathop{max}\limits_{z}(a,b)\mid a\in{A},b\in{B}\} \]

下图中的A是原图，B为A的补集。将A的所有点的灰度值进行平均后乘三（\(3\bar{z}\)），得到的图像与A求交集后得到了图C。

笛卡尔乘积

\[X \times{Y}=\{(x,y)\mid{x\in{X}\ and\ y\in{Y}}\} \]

偏序\(\preceq\)

1. 自反性
2. 反对称性
3. 传递性

严格偏序关系\(\prec\)

1. 反自反性
2. 反对称性
3. 传递性

逻辑操作

空间操作

单像素操作

对单像素进行操作，最简单的就是改变灰度值。

\[s=T(z) \]

\(z\)是像素点的灰度值，\(s\)是经过映射之后的灰度值。

邻域操作

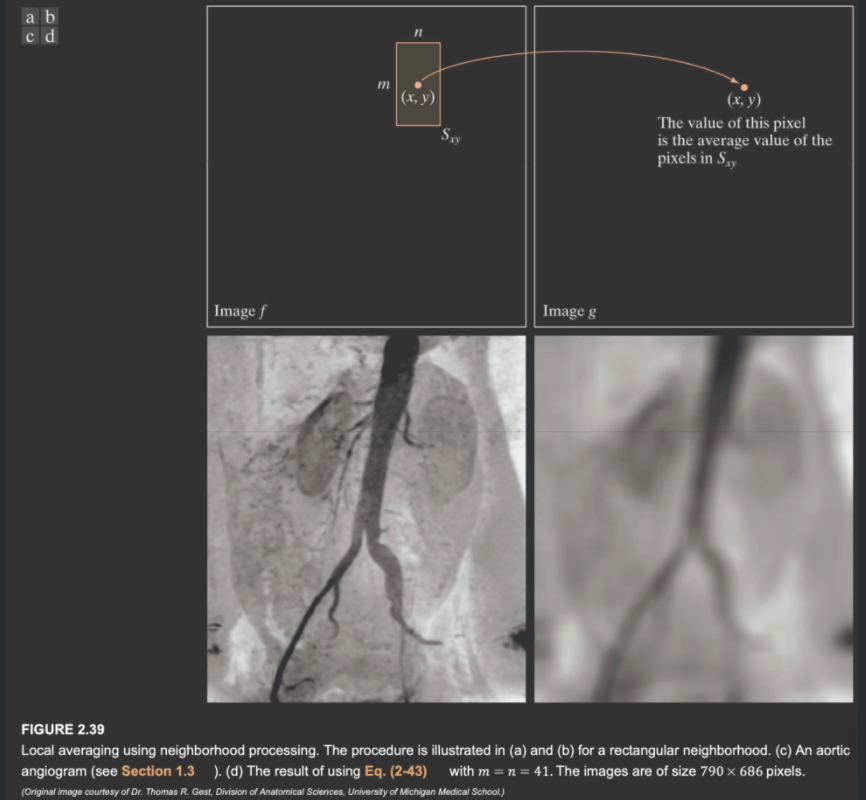
令\(S_{xy}\)为在图像\(f\)以\((x,y)\)为中心的邻域元素集合。邻域操作指的是，在输出图像中的(x,y)生成对应的像素，这个像素是由在原图像中的邻域内，通过一系列的操作得来的。

比如下面的例子，在指定的区域进行求平均操作，最后输出的点就是该点邻域内所有元素灰度值的平均值。

上面的一系列操作可以用下式来表示：

\[g(x,y)=\frac{1}{mn}\sum_{(r,c)\in{S_{sy}}}f(r,c) \]

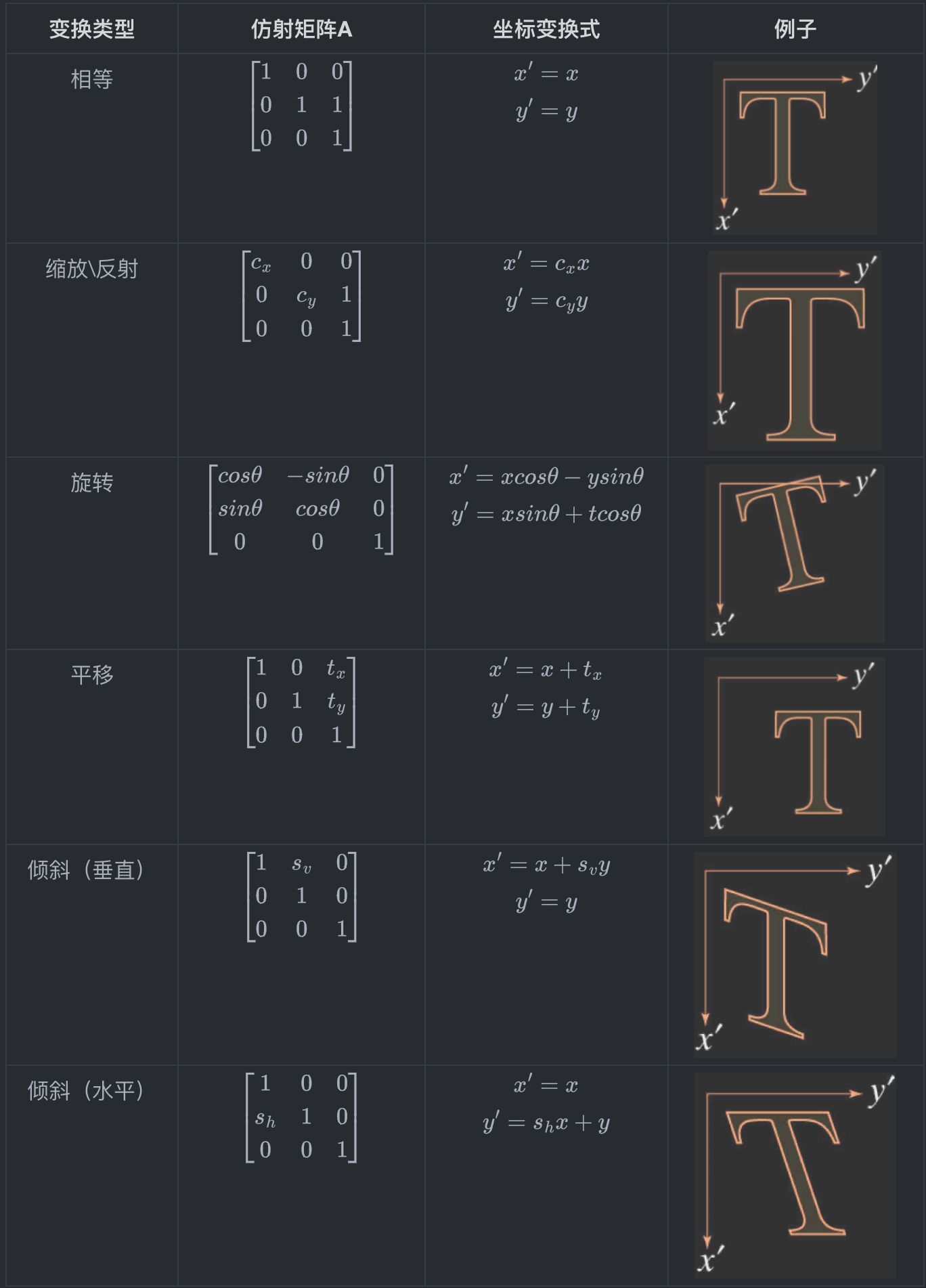
几何变换

图像的几何变换包括两个步骤：

1. 坐标的空间变换；
2. 对空间变换后的像素的灰度值，进行灰度插值。

对图形的几何变换包括：缩放、平移、旋转、裁剪。下面的式子可以表示这四种操作：

\[\begin{bmatrix}x'\\ y'\\1\end{bmatrix}=A\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} \]

下表是不同的操作对应的不同值：

上述过程只是将坐标移动到了新的位置，还需要将像素点的灰度值进行填充。有两种方法进行灰度插值：

1. 正向映射：对于原图像中的每一个点\((x,y)\)，使用\((31)\)直接进行计算。但是这种运算会有几个问题：一是可能多个点的值映射到同一个点，这就需要解决如何解决冲突；二是有可能有的点没有被映射到。
2. 反向映射：对于变换后的图像中的每一个点\((x',y')\)，在原图像中计算\((x,y)=A^{-1}(x',y')\)，然后使用2-4节介绍的技术进行线性插值。

较于正向传播，反向传播效率更高，应用很广。

下面是图像旋转的例子：

图\(a\)为原图，图\(b~d\)分别为：近邻插值法、双线性插值法、三线性插值法。由于边缘缺失了很多过渡的值，\(b\)产生了很多锯齿；\(c\)与\(d\)效果更好，由于从0到255之间多了很多数值来进行过渡，显得更加平滑。虽然在人眼中，c与d没有什么明显差别，但是在进行数据处理时，这种差距还是很重要的。

在进行图像旋转时，可能出现图像旋转后所需要的空间矩形大小大于原始图像的矩形大小的情况。同样有两种做法：一是进行裁剪，二是进行缩放。

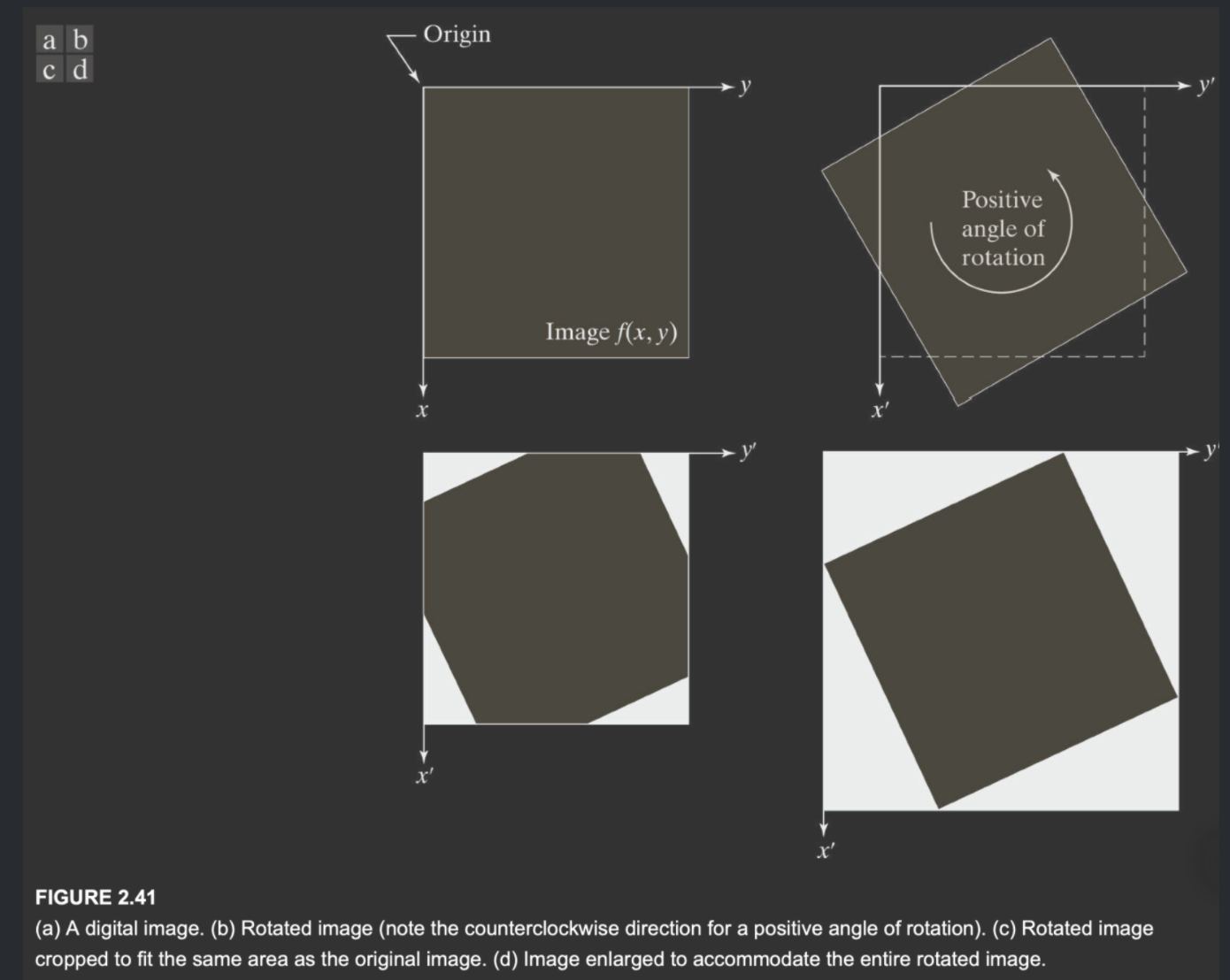
需要注意的是，顺时针角度为负，逆时针为负。

图像配准

图像对准是数字图像处理中的一个重要应用，指的是对齐同一图像中的若干幅图像。下面是一个例子：

首先在输入图像中确定4个锚点，\((v,w)\)是输入，\((x,y)\)是输出，(x,y)由下式确定：

\[x=c_1v+c_2w+c_3vw+c_4\\ y=c_5v+c_6w+c_7vw+c_8 \]

如果找到4组锚点，那么就可以根据上式确定8个式子，就能把\(c_1\)~\(c_8\)解出来。

但是如果4个点不能得到满意的结果，就需要多找一些锚点，然后选择4个锚点组成一个四边形，再使用上面的方法对每个四边形进行变换。变换后，还需要用之前的方法进行灰度插值。

下图\(a\)是原图，\(b\)是拉伸后的图像，小方块是锚点。\(c\)是由\(b\)恢复的图像。d是恢复后的图像与原图像的区别。

图像变换

在某些情况下，图像处理最好变换后再输入图像，在变换域中去执行任务。下面是二维变换的表现形式：

\[T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v) \]

\(f(x,y)\)是输入图像，\(r(x,y,u,v)\)是前向变换核（forward tanshformation kernel），\(T(u,v)\)称为\(f(x,y)\)的前向变换。给定\(T(u,v)\)，则可以用下式的逆变换来求得\(f(x,y)\)：

\[f(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}T(x,y)s(x,y,u,v) \]

\(s(x,y,u,v)\)是反向变换核。

前向变换核是可分离的，如果

\[r(x,y,u,v)=r_1(x,u)r_2(y,v) \]

前向变换核是对称的，如果\(r_1(x,u)=r_2(y,v)\)。

\[r(x,y,u,v)=r_1(x,u)=r_1(y,v) \]

反向变换核也适用上面的定义。

傅立叶变换

数字图像处理中最重要的一种变换就是傅立叶变换，他具有以下正向与反向变换核：

\[r(x,y,u,v)=e^{-j2\pi (ux/M+vy/n)}\\ s(x,y,u,v)=\frac{1}{MN}e^{j2\pi (ux/M+vy/N)} \]

其中\(j=\sqrt{-1}\)。

将上面的\((20)\)与\((21)\)进行替换，得到了

\[T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(ux/M+vy/N)}\\ f(x,y)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}T(u,v)e^{j2\pi(ux/M+vy/N)} \]

可以看出，\((23)\)的两式是对称的且可分离的。

当核是可分的、对称的，并且图像是大小\(M\times M\)时，上式可以使用矩阵表示：

\[T=AFA \]

其中\(F\)是大小为\(M\times M\)的图像矩阵，\(A\)是\(a_{ij}=r_1(i,j)\)的\(M\times M\)矩阵，\(T\)是\(T(u,v)\)的变换结果，大小为\(M\times M\)。

为了得到逆变换，我们在\((24)\)的左右乘上\(B\)：

\[BTB=BAFAB \]

若\(B=A^{-1}\)

\[F=BTB \]

也就是说，F可以完全由正向传播中恢复出来。

概率相关

PDF、PMF、CDF

• PDF（Probability density function）：概率密度函数，连续变量；
• PMF（Probablity density function）：概率质量函数，离散变量；
• CDF（Cumulative distribution function）：累积分布函
  数。

多元高斯PDF

\[p(z)=\frac{1}{(2\pi)^{n/2}\abs{C}^{-1/2}}e^{-\frac{1}{2}[(z-\bar z)^Tc^{-1}(z-\bar z)]} \]

其中\(C\)是\(n\times n\)协方差矩阵，\(c_{ij}\)是\(i\)与\(j\)的协方差

\[C=E[(z-\bar z)(z-\bar z)^T]\\ c_{ij}=E[(z_i-\bar z_i)(z_j-\bar z_j)] \]

多元高斯中的无偏估计

\(\bar z\)de 无偏估计：

\[\bar z=\frac{1}{K}\sum_{k=1}^{K}z_k \]

协方差的无偏估计：

\[C=\frac{1}{K-1}\sum_{k-1}^{K}(z_k-\bar z)(z_k-\bar z)^T \]