2.5 Some Basic Realtionship Between Pixels

Neighbors of a Pixel（邻域）

对于一个像素点\(p(x,y)\)，其垂直与水平的邻居为

\[（x+1,y),(x-1,y),(x,y+1),(x,y-1) \]

这4个邻域使用\(N_4(p)\)来表示。

斜方向的邻域是

\[(x+1,y+1),(x+1,y-1),(x-1,y-1),(x-1,y+1) \]

这4个邻域使用\(N_D(p)\)来表示。

\(p\)的这8个邻域使用\(N_8(p)\)来表示。

Adjacency（邻接）,Connectivity,Regions and Boundaries

使用\(V\)表示定义邻接的灰度值集合。在二值图像中，\(V={1}\)则代表值为1的那些像素具有邻接性。灰度图中道理一样，\(V\)的值可以是0~255中的任何值。对于以下三种情况：

1. 4-邻接，8-邻接：对于两个像素\(p\)和\(q\)，其值都属于\(V\)，如果\(p\)出现在\(q\)的\(N_4(p)\)（\(N_8(p)\)）中，则\(p\)与\(q\)是邻接的。\(p\)和\(q\)称为4（8）邻接。

2. \(m\)-邻接：对于两个像素\(p\)和\(q\)，如果两个像素是\(m\)-邻接的当且仅当：

   a. \(q\)在\(N_4(p)\)中或者:

   b. \(q\)在\(N_D(p)\)中，并且集合${N_4(p)}\cap{N_4(q)} \(中的像素点的值***不***属于\)V$。

比如下图：

在8-邻接的情况下，1同时是2和3 的邻接。但是在m-邻接下，由于不满足条件b（1和2各自的4-邻接存在交集3，且3在V中，所以不满足条件），消除了8-邻接的二义性。

Path

通路

从p到q的一条通路是一系列坐标的集合：

\[(x_0,y_0),(x_1,y_1),\dots ，(x_n,y_n) \]

其中，点\((x_i,y_i)\)和点\((x_{i-1},y_{i-1})\)是邻接的，每个点都不重复，\(1\leq i \leq n\)，\(n\)为通路的长度。如果\((x_0,y_0)=(x_n,y_n)\)则通路为闭合通路。

根据邻接的类型，定义通路为4-通路，8-通路，m-通路。上图中，中为8-通路，右为m-通路。

连通分量与连通集

用S表示一张图片中的一个像素子集。若在像素\(p\)与\(q\)之间存在一条通路，这条路径中的像素点完全由\(S\)中的元素组成，则称\(p\)与\(q\)相连。对于\(S\)中的任意像素\(p\)，在\(S\)中与\(p\)相连的像素集合成为\(S\)的一个连通分量（connected components）。如果只有一个连通分量，则\(S\)成为一个连通集。

区域与区域的邻接性

用\(R\)表示一张图片的一个像素子集。若\(R\)是一个连通集，则称\(R\)为图像的一个区域（\(Region\)）。若两个区域\(R_i\)和\(R_j\)的并集为一个连通集，则称其为邻接的。若区域不邻接，则称为不连通（\(disjoint\))。对于区域的邻接，我们一般只考虑4-邻接与8-邻接。

为了使定义有意义，必须要指定邻接的类型。比如下面这个图，对于4-邻接，就是不连通的两个区域。只有为8-邻接时才连通。

前景与背景

假定一张图片有K个不连通区域\(R_k,k=1,2,\dots,K,\)并且这些区域都不触碰到边缘。用\(R_u\)代表所有的\(K\)个区域的并集，用\((R_u)^c\)代表\(R_u\)的补集，我们称在\(R_u\)中的点为前景，在\((R_u)^c\)中的点为背景。

内边界

区域R的内边界（轮廓）是在R中的点的集合，集合中的点与R的补集中的点邻接。同样，在说明边缘时，也必须指定其邻接性。比如下图，若为4-邻接，则圆圈区域不为轮廓；若为8-邻接，则为边缘。一般来说，使用8-邻接处理类似这种情况。

外边界

大多数算法都是按照外边界来定义的。对于下图这种情况，若使用内边界，则为区域本身，这个边界不是一个闭合路径。但是其外边界却是一条闭合路径。区域的外边界为其补集的内边界。

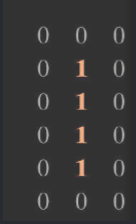
若R为整个图像，则其边界定义为图像的第一行、第一列与最后一行、最后一列的像素集。

Distance Measures

对于像素点\(p,q,s\),其各自的坐标为\((x,y),(u,v),(w,z)\)。D是距离函数，满足以下条件：

a. \(D(p,q)\geq0\) (当\(p=q\)时，\(D(p,q)=0\))

b. \(D(p,q)=D(q,p)\)

c. \(D(p,s)\leq{D(p,q)+D(q,s})\)

p与q的欧式距离定义为

\[D_e(p,q)=[(x-u)^2+(y-v)^2]^\frac{1}{2} \]

距离点\((x,y)\)的欧式距离小于等于\(r\)的点，是以点\((x,y)\)为圆心，半径为r的圆覆盖到的点。

\(D_4\)距离指的是

\[D_4(p,q)=\mid{x-u}\mid+\mid{y-v}\mid \]

距离点\((x,y)\)的\(D_4\)距离小于等于r的点，是一个中心在(x,y)的菱形。

\(D_8\)距离指的是

\[D_8(p,q)=max(\mid{x-u}\mid,\mid{y-v}\mid) \]

距离点\((x,y)\)的\(D_8\)距离小于等于r的点，是一个中心在(x,y)的矩形。

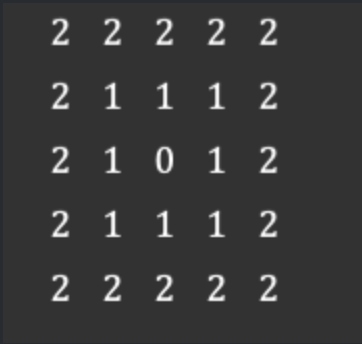
p与q之间的距离与其路径无关。但是，在m-邻接情况下，两点之间的距离被定义为点之间的最短m-路径。比如下面的例子，每个点的值为0或1。

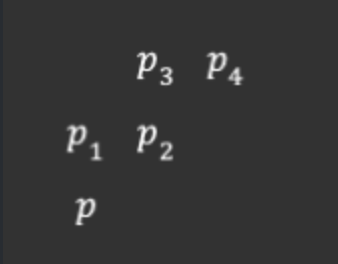
当V={1}时，若\(p_1\),\(p_3\)为0，则p 与\(p_4\)之间的\(D_m\)距离为2（\(p\rightarrow{p_2}\rightarrow{p_4}\));

若\(p_1=1\),则此时\(p_2\)就不再是m-邻接了，\(p\)与\(p_4\)之间的\(D_m\)长度为3(\(p\rightarrow{p_1}\rightarrow{p_3}\rightarrow{p_4}\))。