2.4 Image Sampling and Quantization

图像的采样与量化

大多数传感器的输出都是连续的电压波形，为了得到数字图片，需要将输入进行采样与量化两个过程。

采样与量化的基本概念

图像可以是相对与\(x\)坐标与\(y\)坐标的连续图像，也可以是振幅的连续图像。若要将其数字化，则必须在坐标与振幅中对函数进行采样。将坐标值数字化的过程成为采样，将振幅值数字化的过程成为量化。

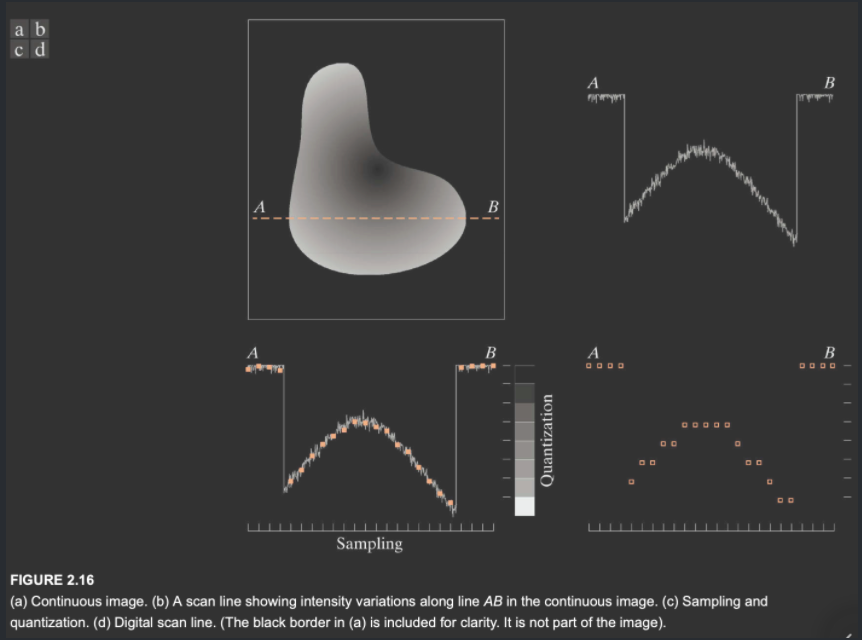
为了将上图中\(AB\)段进行采样，首先从图\(a\)中绘制振幅为函数，然后从图像中，每隔一段距离进行采样，图中的实心方块就是采样的点，并且每个点都是等距的。接下来，由于样本的值仍然在我们量化的范围之外，所以需要根据这些值生成离散函数。在图\(c\)的右边是一个垂直的灰度条，在相应的范围内的点都会被映射为该亮度值。采样后的值如图\(d\)所示。除了所使用的离散电平的数量之外，量化中的精度很大程度上取决于采样信号的噪声多少。

数字图像的表示

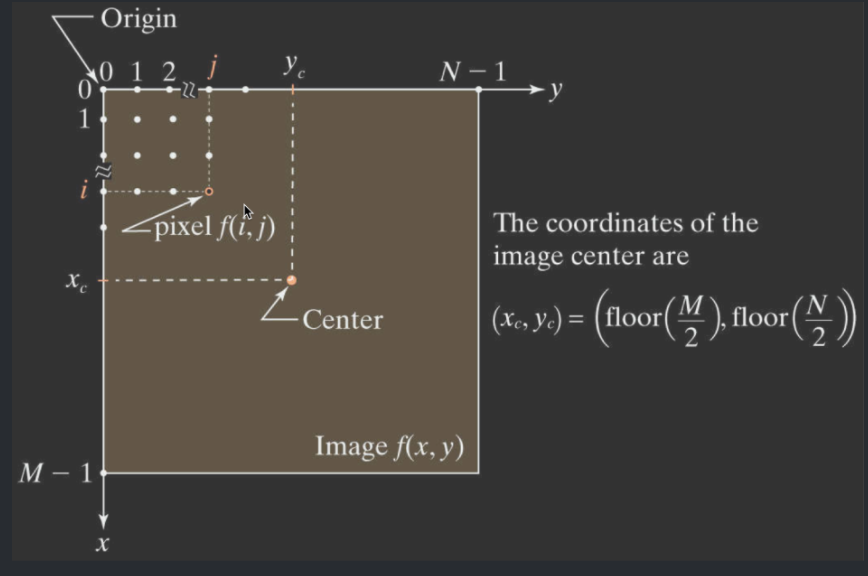
\((x,y)\)表示在平面图像中每一个像素点的坐标，\(f(x,y)\)用来表示这个点上的灰度值。下面是两种表现形式。

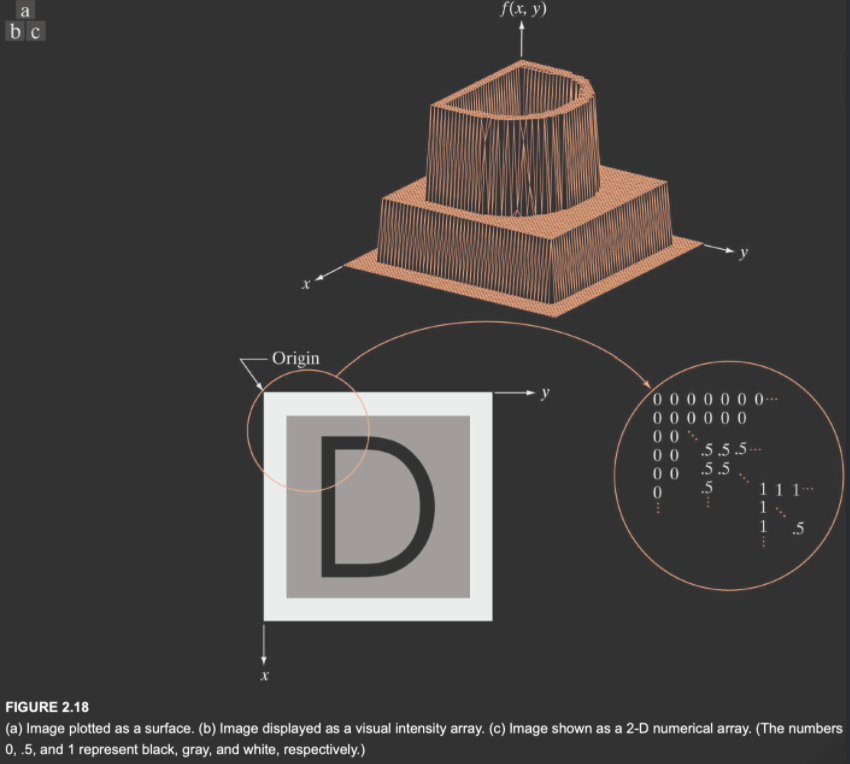
图像也可以用矩阵来表示：

或者更常见的：

线形表示与二维坐标表示

除了用二维坐标系来表示图像，也可以用线形一维来表示：

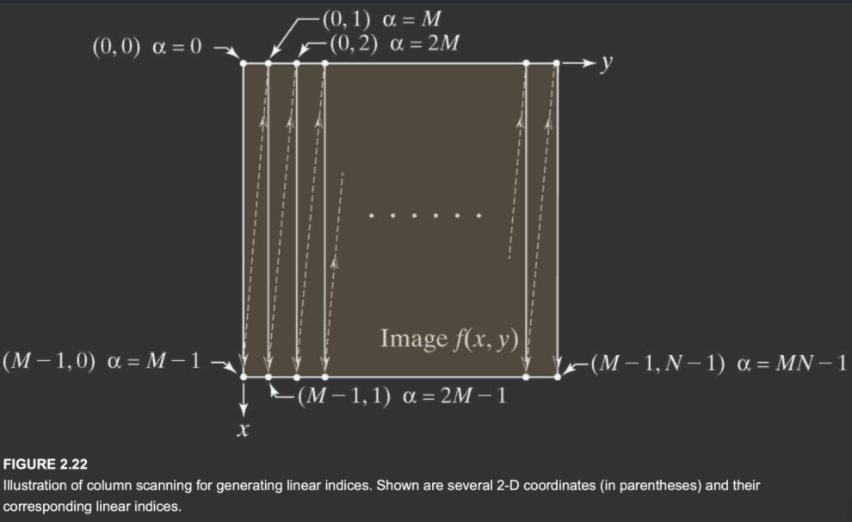
索引的计算：

\[\alpha=2M-1 \]

空间与灰度分辨率

空间分辨率

空间分辨率（spatial resolutiion) 是图象中的最小度量。空间分辨率有两种表示方法：

• 每单位的距离线对数（line pairs per unit distance）
• 每单位距离的像素点数（line pairs per unit distance）

对线对的解释：假设用黑白相间的线来构造一个图，每一条线的线宽为\(W\)，那么每个线对就是\(2W\)，每个单位距离就有\(\frac{1}{2W}\)个线对。广泛使用的图像分辨率的定义是每单位距离的可分辨线对的最大数量。

每单位距离的像素点数是在印刷与出版界广泛使用的测量方法。常用单位：dpi（dots per inch），每英寸像素点数。

空间分辨率必须在基于每单位距离时才有意义。

灰度分辨率

灰度分辨率是指在灰度级中可分辨的最小变化。灰度分辨率是用来量化灰度的比特数，一般都是2的整数次幂，常见的有\(8bits\)，\(16bits\)。

伪轮廓

当灰度分辨率过小时，容易在数字图像灰度平滑区域中造成伪轮廓（False Contouring）。伪轮廓属于数字图像噪声中的一种，主要表现为在数字图像或者视频信号中所呈现的画面平场区域出现明显的类似于等高线的不连续过渡带，从而对于画面感观质量造成影响的现象。如下图：

当图像的灰度分辨率更低时，这种情况更加明显：

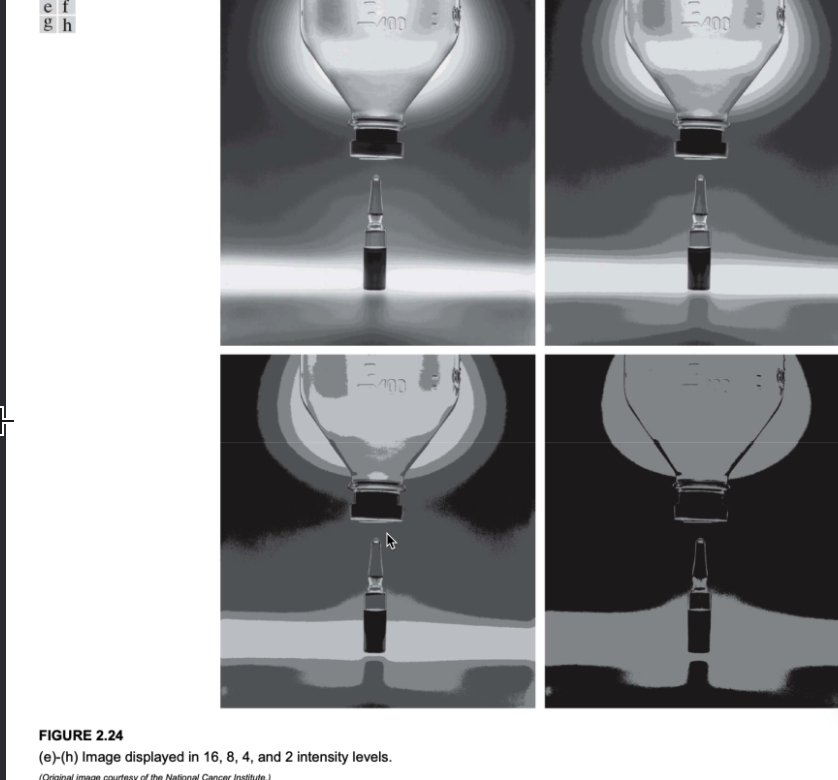
伪轮廓一般出现在16级灰度值（\(4bit\)）或者跟小灰度级的图像中。

图像差值Image Interpolation

图像差值被用来进行缩放、旋转、几何校正等任务。

近邻插值法：假如要把\(500*500\)大小的图像扩大为\(750*750\)大小一种简单的插值方法是：先建立一个\(750*750\)大小的网格，然后将原图像与空白行相继插入网格，然后将图像收缩为源图像大小。这时候，现在的图像相较于之前的原图，像素之间的距离更小了。然后将网格中的插入点进行灰度填充。在原始图像中查找距离待填充的点最近的点，并将这个点的灰度值赋给新点。最后将图像收缩为原来的大小。

但是近插值法容易产生变形，让图像的边缘失真。一种更合适的方法为双线性插值法。

双线性插值法：首先使用\((x,y)\)来代表我们要指定灰度值的像素的坐标。用\(v\)代表该点的灰度值。这个点的灰度值使用下面的式子得出：

\[v(x,y)=ax+by+cxy+d \]

双线性插值法涉及到了坐标的乘法运算，所以其不是线形运算。

四个系数由该点的四个邻居点决定。

双三次差值法

这种方法涉及到一个点的16个邻居点。\((x,y)\)的灰度值由下式决定：

\[v(x,y)=\sum_{i=0}^{3}\sum_{j=0}^{3}a_{ij}x^{i}y^{j} \]

16个系数由16个邻居点确定。如果上式的求和范围变为0~1，则等式3就变为了等式2 。

双三次差值法较于双线性插值法，在保留细节的方面做的更好。双三次插值法是商业图像编辑程序，如PS的使用标准。