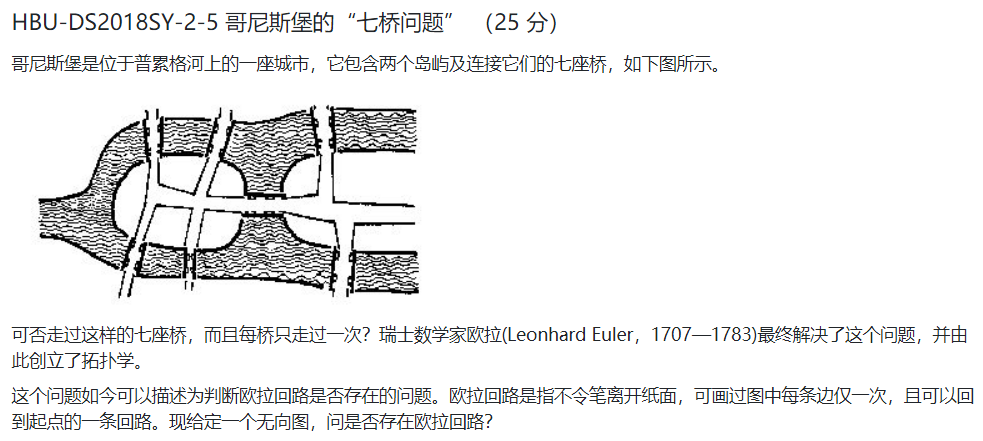
由“哥尼斯堡的‘七桥问题’”引出的并查集问题
最近做了这么一个题目:
题目的意思与一笔画基本一致。给定几个点个几条边,让你判断这个点边构成的无向图是否可以“一笔画”。
欧拉回路有这样一个性质:
若是有向图,则构成欧拉回路的充要条件是每个点的入度等于出度;
若为无向图,则构成欧拉回路的充要条件是每个点的度数为偶数。
这个性质仔细一想就能明白,这里不多做介绍。
这个题麻烦就麻烦在,你并不知道这个图是不是连通的。所以这个题就不是简单的去判断每个点的度数是不是偶数这么简单。我们必须先去判断这个图是否连通。
问题分析:
这里只讨论连通性的求解。
题目实际上是求图的连通分支的个数。只要分支个数大于2,这个图一定不是连通图。求连通分支一个很简单的方式是:并查集。
并查集类似于树的结构。现在我们想:只要拿到了两个节点,我们都为其链接一个“上级”,链接到最后,让根节点的上级是它本身,就完成了一个分支的连接。
下面这个图,每一条就相当于一个分支,每个圆圈就是一个节点。再未完全连接完之前,可能会有很多条这样的分支,在随后的连接中,可能会有一对节点将两条分支连接为一条。到连接结束时,如果有一条分支,则皆大欢喜,要是有两条以上,那对不起咱们不是连通图。
所以说,“并查集”,就是同时对多个分支进行搜索,并在合适的条件下进行合并。查找与合并也就是并查集的核心。
大概意思就是这样,下面我们细致说说这个“并查集”原理到底是如何与怎么操作。

代码分析
并查集主要有一个数组pre[],数组角标是当前节点的编号,数组值是其前驱结点的编号。还有两个函数find(),join()。
我们建立并查集的第一步是进行初始化。因为上面说过,根节点的判断标示就是他的前驱节点是它本身,所以我们初始化就让pre[i]=i,让每个节点的前驱节点都默认为自己。事实上,这相当于让每个节点自成一派,等下面连接的时候再认师傅。
1 void init(int num) 2 { 3 for (int i = 1; i <= num; i++)//num是你的节点数,编号为了方便从1开始 4 { 5 pre[i] = i; 6 } 7 }
接下来就需要去连接各个分支了。因为我们连接分支时,相连通的只需要一个根节点,所以我们在连接的时候需要将一个分支的根节点放在另一个分支的根节点的后面,也就是让一个分支的前驱结点是另一个分支的根节点。

1 void join(int x, int y) 2 { 3 int t1, t2; 4 t1 = find(x);//第一个节点的根节点 5 t2 = find(y);//第二个节点的根节点 6 if (t1 != t2)//两个节点如果不是一个节点的话 7 pre[t2] = t1;//就让t2的前驱结点为t1 8 //也就是,t2节在了t1后面 9 }
那么根节点如何寻找呢?
我们可以使用递归的思想。只要你的前驱结点不是你本身,我就一直向上寻找,直到前驱等于本身为止。代码呼之欲出:
int find(int x) { if (x == pre[x])//如果前驱等于本身 return x;//返回,递归结束 else { //不相等: pre[x] = find(pre[x]);//继续寻找你的前驱节点,向上寻找。 return pre[x];//返回找到的结果。返回x也一样,毕竟是相等才停下来的。 } }
这样我们这个题基本已经出来了,剩下的就是根据题目修改下我们的判断条件:
1 int judge(int num) 2 { 3 int t = 0; //t用来记录根节点的数目 4 for (int i = 1; i <= num; i++)//遍历每个节点 5 { 6 if (pre[i] == i)//如果是根节点 7 t++; 8 if (du[i] % 2 != 0)//如果度数不是偶数 9 return 0;//直接退出,返回假 10 } 11 if (t != 1)//根节点不是一个的话 12 return 0;//就不是连通的了呗 13 return 1;//经历了重重考验,恭喜你,你是连通的 14 }
完整代码:
下面是完整代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 int du[1005]; 4 int pre[1004]; 5 void init(int num) 6 { 7 for (int i = 1; i <= num; i++) 8 { 9 pre[i] = i; 10 } 11 } 12 int find(int x) 13 { 14 if (x == pre[x]) 15 return x; 16 else 17 { 18 pre[x] = find(pre[x]); 19 return pre[x]; 20 } 21 } 22 void join(int x, int y) 23 { 24 int t1, t2; 25 t1 = find(x); 26 t2 = find(y); 27 if (t1 != t2) 28 pre[t2] = t1; 29 } 30 int judge(int num) 31 { 32 int t = 0; 33 for (int i = 1; i <= num; i++) 34 { 35 if (pre[i] == i) 36 t++; 37 if (du[i] % 2 != 0) 38 return 0; 39 } 40 if (t != 1) 41 return 0; 42 return 1; 43 } 44 int main() 45 { 46 int num, count; 47 scanf("%d %d", &num, &count); 48 init(num); 49 int x, y; 50 memset(du, 0, sizeof(du)); 51 52 for (int i = 1; i <= count; i++) 53 { 54 scanf("%d %d", &x, &y); 55 du[x]++; 56 du[y]++; 57 join(x, y); 58 } 59 if (judge(num)) 60 printf("1"); 61 else 62 printf("0"); 63 64 }
通过这个小题目,我发现这个连通集是很高效的算法,很多类似的题目都可以使用这种方式。
最后感谢这个帖子https://blog.csdn.net/u013546077/article/details/64509038