John的农场是一张 N*N 的方格图,贝茜住在左上角(1,1),John住在右下角(N,N)。
现在贝茜要去拜访John,每次都只能往四周与之相邻的方格走,并且每走一步消耗时间 T。
同时贝茜每走三步就要停下来在当前方格吃草,在每个方格吃草的用时是固定的,为 H[i][j]。
John想知道贝茜最少要多久才能到达John的家。
跑一遍djstl。
#include<bits/stdc++.h>
using namespace std;
constexpr int inf = 1e9;
int n, t, h[105][105],d[105][105][5];
int dx[] = {1,-1,0,0,},dy[] = {0,0,1,-1};
struct Pr{
int a, b;
};
queue<Pr> q,q1;
int main(){
cin>>n>>t;
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++){
cin>>h[i][j];
}
for(int i = 0;i < 105;i++){
for(int j = 0;j < 105;j++){
d[i][j][0] = d[i][j][1] = d[i][j][2] = d[i][j][3] = d[i][j][4] = inf;
}
}
q.push({1,1}),q1.push({0,0}),d[1][1][0] = 0;
while(!q.empty()){
for(int i = 0;i < 4;i++){
int x = q.front().a + dx[i],y = q.front().b + dy[i];
if(x > 0 && x <= n && y > 0 && y <= n){
int s = (q1.front().a + 1) % 3,v = q1.front().b
+ t + (!s) * h[x][y];
if(v < d[x][y][s]){
q.push({x,y}),q1.push({s,v}),d[x][y][s] = v;
}
}
}
q.pop(), q1.pop();
}
cout<<min(d[n][n][0],min(d[n][n][1],d[n][n][2]));
}
给定一个完全图,已知两点之间的距离,以及通过某个点的时间(起点和终点不需要花费时间)。你需要回答一些询问,输出两点之间的最短路径,同时需要输出方案。如果有多个方案,输出字典序最小的方案。
数据范围极小,djstl,同时统计一下路径。
一个n点m边无向图,边权均为1,有k个询问
每次询问给出(s,t,d),要求回答是否存在一条从s到t的路径,长度为d
路径不必是简单路(可以自交)
数据保证不存在自环
由于两个点路径距离为d,就一定存在距离为d+2的路径。所以分层图对每个点跑一边spfa求出每个点到其他点经过奇数路径和偶数路径的距离,然后就可以直接判了。
#include<bits/stdc++.h>
#define N 5005
#define INF 0x3f3f3f3f
using namespace std;
template<typename T>inline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
vector<int> t[N];
int n,m,k,tot,h[N];
bool vis[N],ans[1000005];
int dis[2][N];
struct query{
int u,v,w;
}q[1000005];
struct node{
int nex,to;
}edge[N<<1];
inline void add(int u,int v){
edge[++tot].nex=h[u];
edge[tot].to=v;
h[u]=tot;
}
inline void spfa(int s){
queue<int> Q;
for(int i=1;i<=n;i++)dis[0][i]=INF,dis[1][i]=INF,vis[i]=0;
Q.push(s);vis[s]=1;dis[0][s]=0;
while(!Q.empty()){
int x=Q.front();Q.pop();vis[x]=0;
for(int i=h[x];i;i=edge[i].nex){
int xx=edge[i].to,flg=0;
if(dis[0][x]!=INF){
if(dis[1][xx]>dis[0][x]+1)
dis[1][xx]=dis[0][x]+1,flg=1;
}
if(dis[1][x]!=INF){
if(dis[0][xx]>dis[1][x]+1)
dis[0][xx]=dis[1][x]+1,flg=1;
}
if(flg&&!vis[xx])Q.push(xx),vis[xx]=1;
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=1,u,v;i<=m;i++){
read(u);read(v);
add(u,v);add(v,u);
}
for(int i=1;i<=k;i++){
read(q[i].u),read(q[i].v),read(q[i].w);
t[q[i].u].push_back(i);
}
for(int i=1;i<=n;i++){
if(!t[i].size())continue;
spfa(i);
for(int j=0;j<(int)t[i].size();j++){
int o=t[i][j];
int num=q[o].w%2;
if(q[o].w>=dis[num][q[o].v]&&h[i])ans[o]=1;
}
}
for(int i=1;i<=k;i++)
if(ans[i])printf("TAK\n");
else printf("NIE\n");
return 0;
}
D.公路修建问题
OI island是一个非常漂亮的岛屿,自开发以来,到这儿来旅游的人很多。然而,由于该岛屿刚刚开发不久,所以那 里的交通情况还是很糟糕。所以,OIER Association组织成立了,旨在建立OI island的交通系统。 OI island有n 个旅游景点,不妨将它们从1到n标号。现在,OIER Association需要修公路将这些景点连接起来。一条公路连接两 个景点。公路有,不妨称它们为一级公路和二级公路。一级公路上的车速快,但是修路的花费要大一些。 OIER As sociation打算修n-1条公路将这些景点连接起来(使得任意两个景点之间都会有一条路径)。为了保证公路系统的 效率, OIER Association希望在这n-1条公路之中,至少有k条(0≤k≤n-1)一级公路。OIER Association也不希望为 一条公路花费的钱。所以,他们希望在满足上述条件的情况下,花费最多的一条公路的花费尽可能的少。而你的任 务就是,在给定一些可能修建的公路的情况下,选择n-1条公路,满足上面的条件。
输入格式
第一行有三个数n(1≤n≤10000),k(0≤k≤n-1),m(n-1≤m≤20000),这些数之间用空格分开。N和k如前所述,m表示有m对景点之间可以修公路。
以下的m-1行,每一行有4个正整数a,b,c1,c2(1≤a,b≤n,a≠b,1≤c2≤c1≤30000)
表示在景点a与b之间可以修公路,如果修一级公路,则需要c1的花费,如果修二级公路,则需要c2的花费。
形式化:一张图的边有两种边权,求一棵最小生成树使得至少包含k条第一种边。发现形式化题意看完了也就做完了。
显然出题人不希望我们这样做,如果这道题二级公路可以比一级公路贵这种方法就没法做了,所以可以二分答案,然后每次二分往生成树里放k条一级公路。
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5,M=2e4+5;
int fa[N];
struct type {
int u,v,w,t;
int index,choo;
}a[M],b[M];
vector<type> e;
int find(int x){
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
void unite(int x,int y){
fa[find(x)]=find(y);
}
bool cmp(type a,type b){
return a.w<b.w;
}
bool cmp2(type a,type b){
return a.t<b.t;
}
bool cmp3(type a,type b){
return a.index<b.index;
}
int n,k,m,ta,tb;
int tc1,tc2,m1,ans;
int main()
{
cin>>n>>k>>m;
for(int i=1;i<=m-1;i++){
cin>>ta>>tb>>tc1>>tc2;
a[++m1].u=ta,a[m1].v=tb;
a[m1].w=tc2,a[m1].t=tc1,a[m1].index=i;
}
for(int i=1;i<=n;i++) fa[i]=i;
sort(a+1,a+m1+1,cmp2);
int i;
for(i=1;i<=m1&&k;i++){
if(find(a[i].u)!=find(a[i].v)){
unite(a[i].u,a[i].v);
ans=max(ans,a[i].t);
k--;
a[i].choo=1;
e.push_back(a[i]);
}
}
sort(a+i,a+m1+1,cmp);
for(;i<=m1;i++){
if(find(a[i].u)!=find(a[i].v)){
unite(a[i].u,a[i].v);
ans=max(ans,a[i].w);
a[i].choo=2;
e.push_back(a[i]);
}
}
cout<<ans<<endl;
//sort(e.begin(),e.end(),cmp3);
//for(int i=0;i < (int)e.size();i++)
// cout<<e[i].index<<' '<<e[i].choo<<endl;
return 0;
}
吃草
为了庆祝奶牛Bessie的生日,Farmer John给了她一块最好的牧场,让她自由的享用。
牧场上一共有N块草地(1≤N≤1000),编号为1...N,每块草地上牧草的质量都不同。
如果Bessie吃掉的草地上牧草质量为Q,她可以获得Q单位的能量。
每块草地最多和10块草地有相连的道路,在相连的两个草地之间走动需要消耗E单位的能量(1≤E≤1,000,000)。
Bessie可以从任意一块草地开始吃草,并且想要在获得了最多能量的时候停止。
有点遗憾的,Bessie是一头挑食的奶牛,一旦她吃过了一定质量的牧草,她就不会再吃相同或更低质量的牧草!但是她仍然很愿意路过某些草地,而不吃它们。实际上,她发现路过一块高质量的草地而不吃它,等一下返回再去享用,有时会更有利!
请帮忙计算Bessie能够获得的能量的最大值。
发现往返两点之间的最短代价就是最小路径,而最优解的构造方法是从小到大把每块草地的质量排序,然后挨个吃。有的草地吃了它可能会亏,所以就把他踢出去。这样就可以构造一个dp。Fi表示吃第i块草的最大收益。Fi = max(Fj - DISij + VALj)
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 2010;
int n, E;
struct edge{
int to,next,val;
}e[maxn * 10];
int head[maxn];
int cnt;
void addedge(int u,int v){
e[++cnt].to = v;
e[cnt].val = E;
e[cnt].next = head[u];
head[u] = cnt;
}
int dis[maxn][maxn];
bool vis[maxn];
struct node{
int dis,pos;
bool operator<(const node x) const{
return dis > x.dis;
}
};
constexpr int inf = 1e9;
void djstl(int S){
priority_queue<node> q;
for(int i = 0;i < maxn;i++) dis[S][i] = inf,vis[i] = false;
q.push((node){0,S});
dis[S][S] = 0;
while(!q.empty()){
node temp = q.top();
q.pop();
int x = temp.pos;
if(vis[x]) continue;
vis[x] = true;
for(int i = head[x];i;i = e[i].next){
int y = e[i].to;
if(dis[S][x] + e[i].val < dis[S][y]){
dis[S][y] = dis[S][x] + e[i].val;
if(!vis[y]){
q.push((node){dis[S][y],y});
}
}
}
}
}
void getdis(){
for(int i = 1;i <= n;i++){
djstl(i);
}
}
int dp[maxn];
struct grass{
int val,cur;
bool operator <(grass x) const{
return val < x.val;
}
}grass[maxn];
int main(){
cin>>n>>E;
for(int i = 1;i <= n;i++){
int q,d;
cin>>q>>d;
grass[i].val = q;
grass[i].cur = i;
for(int j = 1;j <= d;j++){
int v;
cin>>v;
addedge(i,v);
}
}
getdis();
for(int i=0;i<=n;++i)
dis[0][i]=0;
sort(grass+1,grass+n+1);
for(int i = 1;i <= n;i++) dp[i] = grass[i].val;
int ans = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j < i;j++){
dp[i] = max(dp[i],dp[j] - dis[grass[j].cur][grass[i].cur]+grass[i].val);
}
ans = max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}
最优贸易
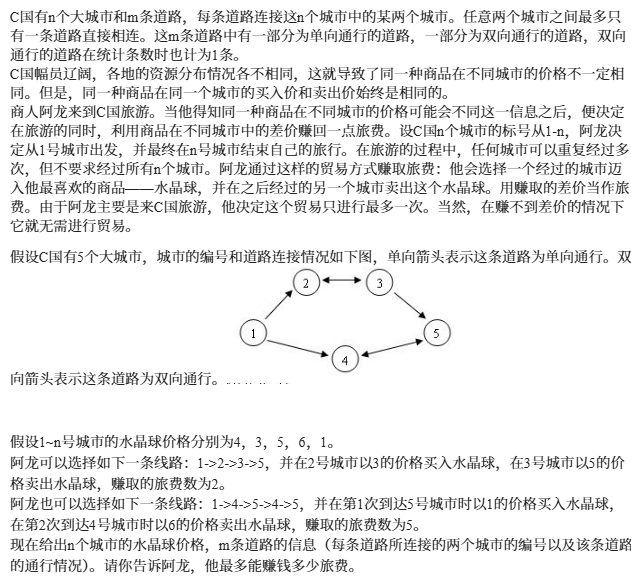
tarjan缩点,缩完之后从出发点求一遍前缀最大价格,从目的地往前求一遍后缀最小价格。枚举每个节点两个值一减就是答案。
记忆宫殿

初始入度为\(0\)的点为源点。
我们令 \(S\) 为如果成立,就能够推出事件的源点集合。
当事件成立时,显然 \(S\) 中的点必有至少一个是真的。所以我们只要把所有包含 \(S\) 的事件都标记为真就行了。
Pro-Professor Szu
某大学校内有一栋主楼,还有 栋住宅楼。这些楼之间由一些单向道路连接,但是任意两栋楼之间可能有多条道路,也可能存在起点和终点为同一栋楼的环路。存在住宅楼无法到达主楼的情况。
现在有一位古怪的教授,他希望每天去主楼上班的路线不同。
一条上班路线中,每栋楼都可以访问任意多次。我们称两条上班路线是不同的,当且仅当两条路线中存在一条路是不同的(两栋楼之间的多条道路被视为是不同的道路)。
现在教授希望知道,从哪些住宅楼前往主楼的上班路线数最多。
到达n+1后,可以选择停下或者继续走
首先发现若一个大小大于 1 的 SCC 或自环(下称为不合法结构)能够到达教学楼,则该不合法结构内部每个点到教学楼的路径数量都是无穷大。
显然可以先缩点,然后拓扑排序。
先将反图上入度为 0 的非教学楼点入队跑一遍拓扑排序。注意此时不合法结构可以入队,因为它们没有到达教学楼的路径。
最后,若出现没有入队的点,说明这个点能够到达一个不合法结构,因此路径数同样为无穷大。此外,若 \(f_i>36500\) 也不符合题意。
自己的代码没调出来,一直不过hack,贴一个题解的,过了就补(已)
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, m, ed, ban[N], deg[N], f[N];
int dn, dfn[N], low[N], cn, col[N], top, stc[N], vis[N];
struct linklist {
int cnt, hd[N], nxt[N], to[N];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
} e, g;
void tarjan(int id) {
dfn[id] = low[id] = ++dn, stc[++top] = id, vis[id] = 1; // 0 -> 1
for(int _ = e.hd[id]; _; _ = e.nxt[_]) {
int it = e.to[_];
if(!dfn[it]) tarjan(it), low[id] = min(low[id], low[it]);
else if(vis[it]) low[id] = min(low[id], dfn[it]);
}
if(low[id] == dfn[id]) {
col[id] = ++cn, ban[cn] = stc[top] != id;
while(stc[top] != id) col[stc[top]] = cn, vis[stc[top--]] = 0; // id -> cn
vis[id] = 0, top--;
}
}
int main() {
#ifdef ALEX_WEI
freopen("1.in", "r", stdin);
freopen("1.out", "w", stdout);
#endif
cin >> n >> m;
for(int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
e.add(u, v);
}
for(int i = 1; i <= n + 1; i++) if(!dfn[i]) tarjan(i);
for(int i = 1; i <= n + 1; i++)
for(int _ = e.hd[i]; _; _ = e.nxt[_]) {
int it = e.to[_];
if(i == it) ban[col[i]] = 1;
else if(col[i] != col[it]) g.add(col[it], col[i]), deg[col[i]]++;
}
ed = col[n + 1];
queue<int> q;
for(int i = 1; i <= cn; i++) if(i != ed && !deg[i]) q.push(i);
memset(vis, 0, sizeof(vis));
while(!q.empty()) {
int t = q.front();
q.pop(), vis[t] = 1;
for(int _ = g.hd[t]; _; _ = g.nxt[_]) {
int it = g.to[_];
if(!--deg[it] && it != ed) q.push(it);
}
}
if(!ban[ed]) assert(!deg[ed]), q.push(ed), f[ed] = 1;
while(!q.empty()) {
int t = q.front();
q.pop(), vis[t] = 1;
for(int _ = g.hd[t]; _; _ = g.nxt[_]) {
int it = g.to[_];
if(ban[it]) continue;
f[it] = min(36501, f[it] + f[t]);
if(!--deg[it]) q.push(it);
}
}
vector<int> ans;
for(int i = 1; i <= n; i++)
if(!vis[col[i]] || f[col[i]] == 36501)
ans.push_back(i);
if(!ans.empty()) puts("zawsze");
else {
int mx = 0;
for(int i = 1; i <= n; i++) {
if(f[col[i]] > mx) mx = f[col[i]], ans.clear();
if(f[col[i]] == mx) ans.push_back(i);
}
cout << mx << "\n";
}
cout << ans.size() << "\n";
for(int it : ans) cout << it << " ";
return cerr << "Time: " << clock() << endl, 0;
}

