2024.11.12 总结
D.公路修建问题
OI island是一个非常漂亮的岛屿,自开发以来,到这儿来旅游的人很多。然而,由于该岛屿刚刚开发不久,所以那 里的交通情况还是很糟糕。所以,OIER Association组织成立了,旨在建立OI island的交通系统。 OI island有n 个旅游景点,不妨将它们从1到n标号。现在,OIER Association需要修公路将这些景点连接起来。一条公路连接两 个景点。公路有,不妨称它们为一级公路和二级公路。一级公路上的车速快,但是修路的花费要大一些。 OIER As sociation打算修n-1条公路将这些景点连接起来(使得任意两个景点之间都会有一条路径)。为了保证公路系统的 效率, OIER Association希望在这n-1条公路之中,至少有k条(0≤k≤n-1)一级公路。OIER Association也不希望为 一条公路花费的钱。所以,他们希望在满足上述条件的情况下,花费最多的一条公路的花费尽可能的少。而你的任 务就是,在给定一些可能修建的公路的情况下,选择n-1条公路,满足上面的条件。
输入格式
第一行有三个数n(1≤n≤10000),k(0≤k≤n-1),m(n-1≤m≤20000),这些数之间用空格分开。N和k如前所述,m表示有m对景点之间可以修公路。
以下的m-1行,每一行有4个正整数a,b,c1,c2(1≤a,b≤n,a≠b,1≤c2≤c1≤30000)
表示在景点a与b之间可以修公路,如果修一级公路,则需要c1的花费,如果修二级公路,则需要c2的花费。
形式化:一张图的边有两种边权,求一棵最小生成树使得至少包含k条第一种边。发现形式化题意看完了也就做完了。
显然出题人不希望我们这样做,如果这道题二级公路可以比一级公路贵这种方法就没法做了,所以可以二分答案,然后每次二分往生成树里放k条一级公路。
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5,M=2e4+5;
int fa[N];
struct type {
int u,v,w,t;
int index,choo;
}a[M],b[M];
vector<type> e;
int find(int x){
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
void unite(int x,int y){
fa[find(x)]=find(y);
}
bool cmp(type a,type b){
return a.w<b.w;
}
bool cmp2(type a,type b){
return a.t<b.t;
}
bool cmp3(type a,type b){
return a.index<b.index;
}
int n,k,m,ta,tb;
int tc1,tc2,m1,ans;
int main()
{
cin>>n>>k>>m;
for(int i=1;i<=m-1;i++){
cin>>ta>>tb>>tc1>>tc2;
a[++m1].u=ta,a[m1].v=tb;
a[m1].w=tc2,a[m1].t=tc1,a[m1].index=i;
}
for(int i=1;i<=n;i++) fa[i]=i;
sort(a+1,a+m1+1,cmp2);
int i;
for(i=1;i<=m1&&k;i++){
if(find(a[i].u)!=find(a[i].v)){
unite(a[i].u,a[i].v);
ans=max(ans,a[i].t);
k--;
a[i].choo=1;
e.push_back(a[i]);
}
}
sort(a+i,a+m1+1,cmp);
for(;i<=m1;i++){
if(find(a[i].u)!=find(a[i].v)){
unite(a[i].u,a[i].v);
ans=max(ans,a[i].w);
a[i].choo=2;
e.push_back(a[i]);
}
}
cout<<ans<<endl;
//sort(e.begin(),e.end(),cmp3);
//for(int i=0;i < (int)e.size();i++)
// cout<<e[i].index<<' '<<e[i].choo<<endl;
return 0;
}
吃草
为了庆祝奶牛Bessie的生日,Farmer John给了她一块最好的牧场,让她自由的享用。
牧场上一共有N块草地(1≤N≤1000),编号为1...N,每块草地上牧草的质量都不同。
如果Bessie吃掉的草地上牧草质量为Q,她可以获得Q单位的能量。
每块草地最多和10块草地有相连的道路,在相连的两个草地之间走动需要消耗E单位的能量(1≤E≤1,000,000)。
Bessie可以从任意一块草地开始吃草,并且想要在获得了最多能量的时候停止。
有点遗憾的,Bessie是一头挑食的奶牛,一旦她吃过了一定质量的牧草,她就不会再吃相同或更低质量的牧草!但是她仍然很愿意路过某些草地,而不吃它们。实际上,她发现路过一块高质量的草地而不吃它,等一下返回再去享用,有时会更有利!
请帮忙计算Bessie能够获得的能量的最大值。
发现往返两点之间的最短代价就是最小路径,而最优解的构造方法是从小到大把每块草地的质量排序,然后挨个吃。有的草地吃了它可能会亏,所以就把他踢出去。这样就可以构造一个dp。Fi表示吃第i块草的最大收益。Fi = max(Fj - DISij + VALj)
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 2010;
int n, E;
struct edge{
int to,next,val;
}e[maxn * 10];
int head[maxn];
int cnt;
void addedge(int u,int v){
e[++cnt].to = v;
e[cnt].val = E;
e[cnt].next = head[u];
head[u] = cnt;
}
int dis[maxn][maxn];
bool vis[maxn];
struct node{
int dis,pos;
bool operator<(const node x) const{
return dis > x.dis;
}
};
constexpr int inf = 1e9;
void djstl(int S){
priority_queue<node> q;
for(int i = 0;i < maxn;i++) dis[S][i] = inf,vis[i] = false;
q.push((node){0,S});
dis[S][S] = 0;
while(!q.empty()){
node temp = q.top();
q.pop();
int x = temp.pos;
if(vis[x]) continue;
vis[x] = true;
for(int i = head[x];i;i = e[i].next){
int y = e[i].to;
if(dis[S][x] + e[i].val < dis[S][y]){
dis[S][y] = dis[S][x] + e[i].val;
if(!vis[y]){
q.push((node){dis[S][y],y});
}
}
}
}
}
void getdis(){
for(int i = 1;i <= n;i++){
djstl(i);
}
}
int dp[maxn];
struct grass{
int val,cur;
bool operator <(grass x) const{
return val < x.val;
}
}grass[maxn];
int main(){
cin>>n>>E;
for(int i = 1;i <= n;i++){
int q,d;
cin>>q>>d;
grass[i].val = q;
grass[i].cur = i;
for(int j = 1;j <= d;j++){
int v;
cin>>v;
addedge(i,v);
}
}
getdis();
for(int i=0;i<=n;++i)
dis[0][i]=0;
sort(grass+1,grass+n+1);
for(int i = 1;i <= n;i++) dp[i] = grass[i].val;
int ans = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j < i;j++){
dp[i] = max(dp[i],dp[j] - dis[grass[j].cur][grass[i].cur]+grass[i].val);
}
ans = max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}
最优贸易
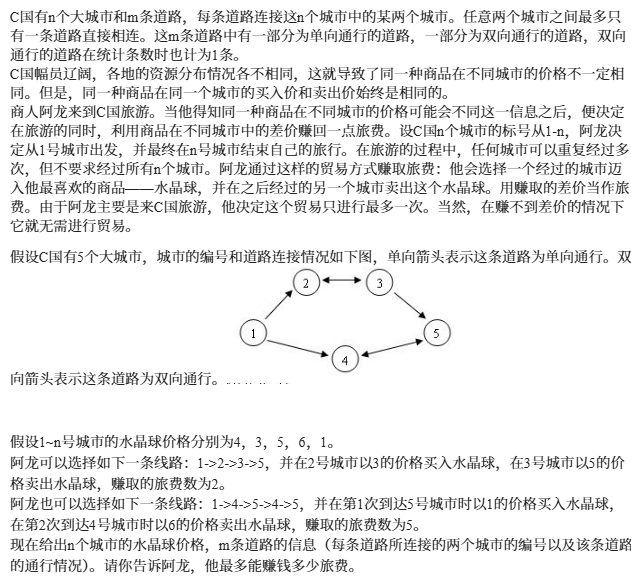
tarjan缩点,缩完之后从出发点求一遍前缀最大价格,从目的地往前求一遍后缀最小价格。枚举每个节点两个值一减就是答案。



