10.4 笔记
[NOIP2021] 方差

我的乱搞:
首先将序列做一个差分,一次操作实际上就是在交换差分数组的相邻两项。模随机化,每次随机交换两个元素,得分80.
再优化一下,把交换元素改为插入元素。由于要方差最小,而方差最小的序列差分一定是先下降后上升的,而最优的交换方案一定是将序列下降一侧的元素插到上升一侧并且保持上升的一侧仍然保持上升的方案。
模拟退火,使用stl双端队列插入,吸氧跑得飞快。
再调一调参数,就可以A了。
code:
#include<bits/stdc++.h>
#define ll long long
const int maxn = 1e4+9;
using namespace std;
typedef deque<int>::iterator iter;
int a[maxn],b[maxn],mini=2147483647,n;
deque<int> que;
iter lpt,rpt;
ll ans;
string s = "214748364721474836472147483647214748364721474836472147483647217483647217483647";
int seed(){
int res = 0;
for(int i = 0;i < (int)s.length();i++){
res += (int)s[i];
}
return res;
}
mt19937 rnd((int)seed());
void Init();
void Read(){
scanf("%d",&n);
for(int i=0; i<n; i++){
scanf("%d",&a[i]);
a[i]*=n;
}
for(int i=0; i<n-1; i++){
b[i]=a[i+1]-a[i];
}
Init();
}
void Init(){
sort(b,b+n-1);
bool f=0;
for(int i=0; i<n-1; i++){
mini = min(mini,b[i]);
if(f) que.push_front(b[i]);
else que.push_back(b[i]);
f = !f;
}
f=0;
for(int i=0; i<n-1; i++){
if(que[i]==mini){
if(!f){
lpt = que.begin()+i;
rpt = que.begin()+i;
f=1;
} else {
rpt = que.begin()+i;
}
}
}
}
ll calc(){
ll sum=0,cur=0,pj,fc;
for(int solo : que){
cur += solo;sum += cur;
}
pj = sum/n;
fc = pow(pj,2);
cur = 0;
for(int solo : que){
cur += solo;fc += pow(cur-pj,2);
}
return fc/n;
}
void SA(){
double T = 3e3;
ll now=ans,newans,de;
int rndsize = n-1-(rpt-lpt+1),val,len=rpt-lpt+1;
iter A;
while(T>1e-5){
for(int i=0; i<n-1; i++){
if(que[i] == mini){
lpt = que.begin()+i;rpt = lpt+len-1;
break;
}
}
deque<int> tmp = que;
A = que.begin()+(rnd()%rndsize);
if(A >= lpt){
A += len;val = *A;
que.erase(A);
iter now = que.begin();
while(*now > val) now++;
que.insert(now,val);
} else {
val = *A;
que.erase(A);
iter now = que.end();
while(*(now-1) > val) {
now--;
}
que.insert(now,val);
}
newans = calc(); de=newans-now;
if(de<0 || exp(-de/T)*2147483647*2>rnd()) {
ans = min(ans,newans);
now = newans;
} else que = tmp;
T*=0.97;
}
}
int main(){
Read();
ans = calc();
if(rpt-lpt+1 == n-1) printf("%lld",ans);
else {
clock_t s = clock();
SA();
clock_t len = clock()-s, limit = CLOCKS_PER_SEC*0.975;
while(clock()+len < limit) SA();
printf("%lld",ans);
}
return 0;
}
再讲正解
初中老师曾经没讲过,方差的一种计算方式是平方的期望减去期望的平方,也就是:
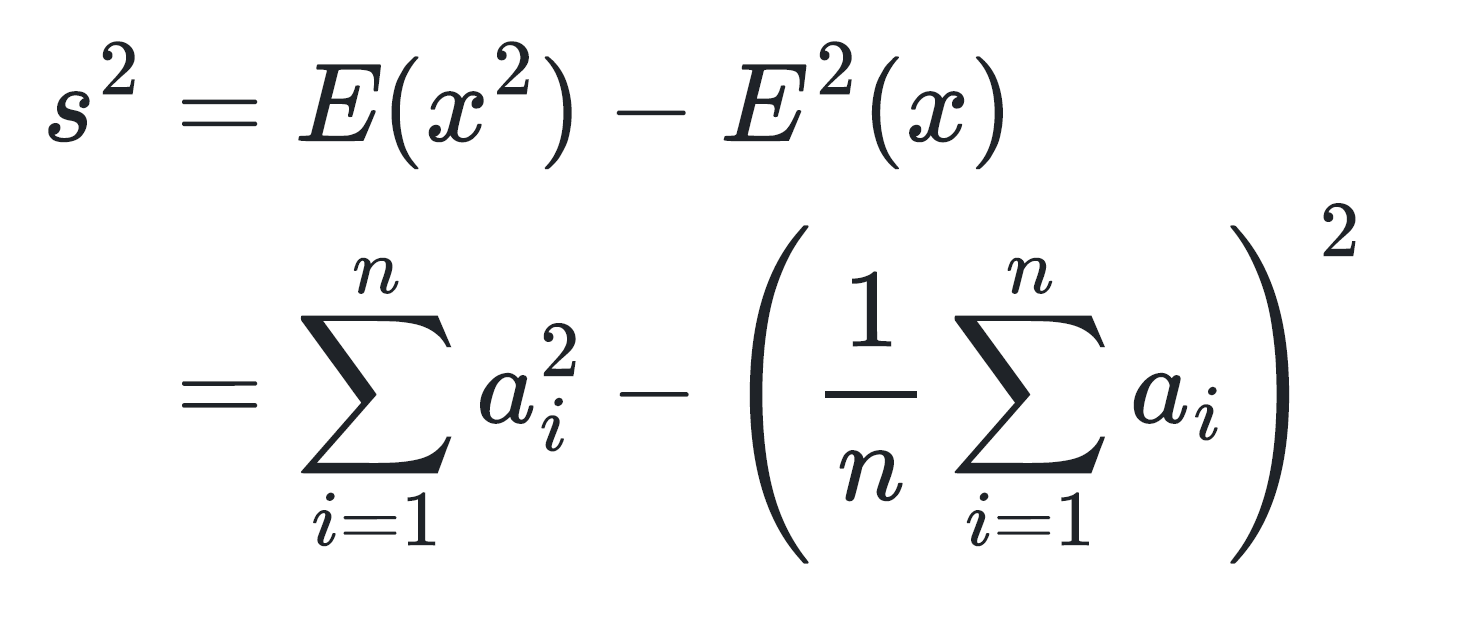


好吧其实我并不会打正解
Luogu P5249 [LnOI2019]加特林轮盘赌


光线

多层玻璃可以看作一层,所以有可能通过前i-1层玻璃的透光率求出这一层玻璃的透光率。
但是,现在有反射率这个玩意。
光线有可能再任意两块玻璃之间无限反射,并且第一面和最后一面射入的光的反射率是不相同的。
总之,我们需要维护两个量:
前 i 面玻璃按顺序叠在一起后,光从第 1 面玻璃射入时的透光率。
前 i 面玻璃按顺序叠在一起后,光从第 i 面玻璃射入时的反射率。
然后根据兔队的《不难推出》,就得到了这两个式子:
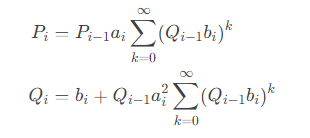
由于\(|a| < 1\)时,这个无穷级数等于1/1-a
所以