[CCO2017] 接雨滴
题目描述
晚上,夜黑风高,大雨疯狂地从天而降。
Lucy 想要接住一些雨滴,但她只有有限的工具。她有一套不同高度的柱子来接住雨滴。每根柱子的高度为整数,宽度为
举个例子,如果 Lucy 有高度分别为
*
* *
* *
** *
*****
这样会接住
为了方便表述,我们定义
*
*RR*
*RR*
**R*
*****
当然了,她也可以这样摆放柱子,这样可以接住
*
*RR*
*RR*
**RR*
*****
再举一个例子,如果柱子的高度分别为
*R*R*
*R*R*
*R*R*
*R*R*
*****
最后一个例子,如果柱子的高度分别为
*RRR*
*R*R*
*R*R*
*R*R*
*****
Lucy 有
slove
结论:对于某个柱子 x 上方的积水体积,可能产生的所有体积都是合法的。
证明:
首先,形成积水肯定需要两个高柱子,即最高柱和次高柱。我们先放好。接着,我们要插入一个柱子
1)若我们想让x上方没有积水
我们找到柱子
我们再找一个比
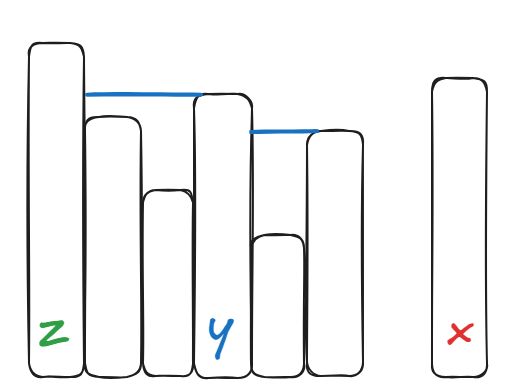
https://excalidraw.com/
将
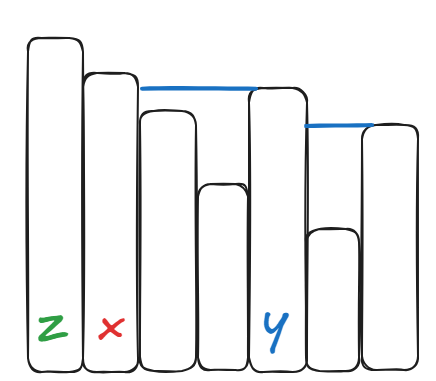
因为我们找到的
在
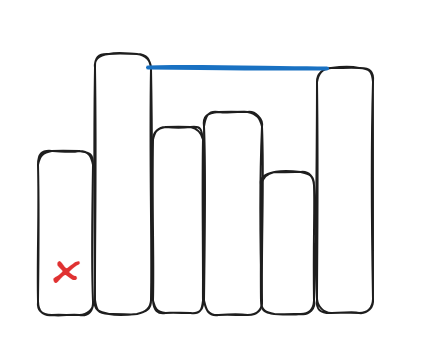
因此,一定有一种方案使得插入x后总共先不变。
2)设有一个比他高的柱子
1.如果y没有被积水覆盖
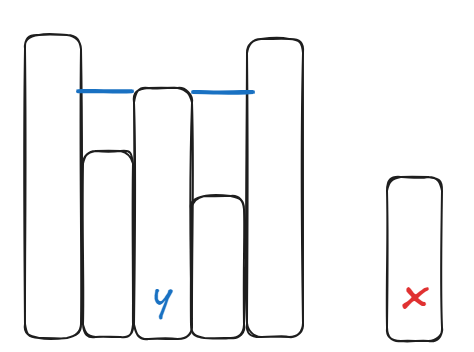
除非
2.如果
找到一个离
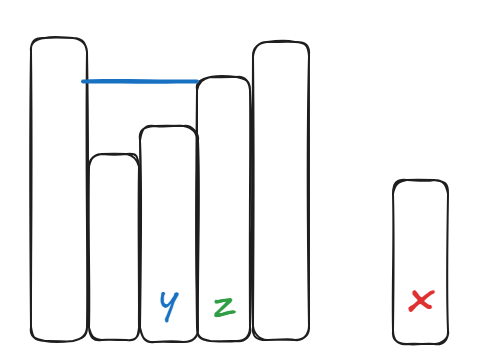
我们把
3)如果
综上,对于某个柱子
背包转移,bitset优化。
using namespace std;
const int maxN=5e2+5,maxH=5e1+5;
int a[maxN];
bitset<maxN*maxH>dp,tem;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
dp[0]=true;
for(int j=1;j<n;++j)
{
for(int st=j+1;st<n;++st)
{
tem|=(dp<<(a[st]-a[j]));
}
dp|=tem;
}
for(int i=0;i<=25000;++i)
{
if(dp[i])
{
printf("%d ",i);
}
}
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现