2024/7/10 笔记
CF1693F
对0,1个数相等的0,1串进行排序一定是最优的贪心策略。
我们把0记为1，1记为-1.求前缀和
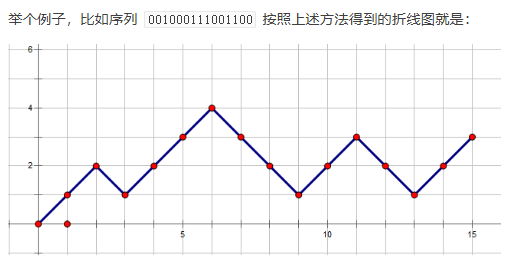
如果1的个数大于0的个数，那么就把整个串翻转然后取反，推一下就可以知道结果不会变。
CF1646F
这题我写了半天发现假了；
一开始看了样例很容易想到，每个人每轮都把自己不需要的牌往下放，由于操作数不能超过n^2-n,我还特地为每个人开了一个优先队列，按dis（当前牌还有多远（经过多少轮）才能到达他应该到的那个人），然后每次取出dis最小的下发。
这时我犯了第一个错误，每轮每个人的操作是同时进行的，而如果用循环实时更新的话，就会导致上一个人刚放下来的牌被下一个人取走，同一轮中这种情况是显然不会出现的。所以我又整了两个栈来把每一轮的修改存起来。
但我发现还是不不对
仔细思考，我发现到最后有可能某一个人的牌已经达成目标了但其他人手里还有不需要的牌，这种情况就很难处理。如果那个牌凑齐了的人把自己的一张牌下发的话，就有可能造成死循环，而其他策略我有没有找到其他可行的方法，遂放弃。
看了题解，才恍然大悟。
using namespace std;
const int maxn = 150;
int xl[maxn*maxn][maxn],mp[maxn][maxn],dq[maxn],dq1[maxn],n,col,tot,cnt[maxn];
void add(int x,int y){
mp[x][y]++,cnt[x]+=(mp[x][y]==1);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
cin>>col,add(i,col);
}
for(int i=1;i<=n*(n-1)/2;i++){
int pd=1;
for(int j=1;j<=n;j++)
if(cnt[j]!=n) {pd=0; break;}
if(pd) break;
tot++; int cs=0;
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++)
if(mp[j][k]>1) {cs=j; break;}
if(cs) break;
}
for(int j=cs;j<=n;j++)
for(int k=1;k<=n;k++)
if(mp[j][k]>1) {xl[tot][j]=k,mp[j][k]--,add(j%n+1,k); break;}
for(int j=1;j<=cs-1;j++)
for(int k=1;k<=n;k++)
if(mp[j][k]>1) {xl[tot][j]=k,mp[j][k]--,add(j%n+1,k); break;}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) dq[j]=(i+j-2)%n+1;
for(int j=1;j<=i-1;j++){
tot++;
for(int j=1;j<=n;j++) xl[tot][j]=dq[j],dq1[j%n+1]=dq[j];
for(int k=1;k<=n;k++) dq[k]=dq1[k];
}
}
cout<<tot<<endl;
for(int i=1;i<=tot;i++){
for(int j=1;j<=n;j++) cout<<xl[i][j]<<" ";
cout<<endl;
}
return 0;
}
CF741C
正解是二分图染色；
乱搞做法（与题解雷同）只不过我没有暴力搞成121212而是先按两人的冲突分配成不同的1/2
