SHAPEIT算法简介

　　本文是基于SHAPIT2和SHAPEIT4的，先介绍SHAPEIT2的算法原理，然后简单介绍了一下SHAPEIT4更新的部分。文中介绍主要集中在算法部分，比较简介，具体内容请看参考文献。

　　[SHAPEIT2的参考文献为：a linear complexity phasing method for thousands of genomes；SHAPIT4的参考文献为：Accurate, scalable and integrative haplotype estimation]

　　相比于其他单体型分型软件，SHAPEIT2一共有两个改进，第一个改进是压缩，第二个改进是抽样。

　　压缩部分：

　　设定G为一个独立个体的基因型(genotype)，H为除了这个个体以外的其他样本的单体型(haplotype)，H和G涉及到的SNP相同。这里的H，说是其他个体的单体型，但是在计算刚开始的时候其他个体的单体型并不是已知的。所以在计算刚开始的时候是列举其他个体所有满足基因型G的单体型，然后从其中随机选取单体型作为已知的单体型，组成单体型集合H。在该情况下，推测独立个体的基因型，即推测出符合G的约束的两个单体型，即P(h|H)。

　　

 

 

 　　图1

　　在该方法中，对图H进行压缩，构建CHMM，即压缩隐马尔可夫模型。在原图H中，假设有K个单体型，涉及M个SNP，图2即压缩后的图H_g。压缩方法：在M个SNP中随机选择一个点作为起始点，给定一个压缩后的单体型个数J(J<M)，在起始点左边，从左到右，逐个合并SNP，把在这些SNP范围内的单体型进行合并，知道合并后的单体型个数最接近J，这一部分算作一个片段(segment)。当合并后单体型个数最接近J时，断开segment，从接下来的一个SNP继续按此方法进行单体型合并，以此进行，直到把起始点合并进一个segment。在起始点的右边，从右向左进行合并，合并方法与左边类似。直到包含起始点。

　　

 

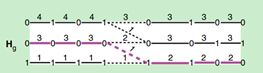
图2

　　在图H_g中，每个点和每个边均被赋予权重，权重分别为穿过该点和边的单体型的个数，分别记作c(k_m)和c(k_m,k_m+1)。每个点和边都至少有一个单体型穿过，并且H中的每个单体型在H_g中都有唯一路径。

　　压缩后的图去除了单体型的局部冗余，并且即使样本量增加或SNP增加，图的大小仍在一定范围内，图中的节点个数为JM个。完成压缩后，不再基于H图建立隐马模型，而是基于H_g建立模型，即P(h|h_g)。则有M个隐藏状态z={z₁,...,z_m,...z_M}，和M个观测状态{h₁,..,h_m,...,h_M}，这M个观测状态即为H_g中表示的单体型。

　　基于H_g的隐马模型，其参数为：

　　起始状态概率：

　　

 

 

 　　状态转移概率：

　　

 

 

 　　

 

 　　状态发射概率：

　　

 

　　

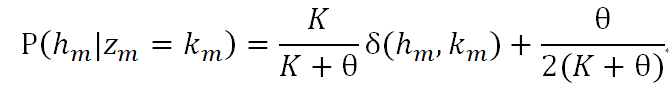
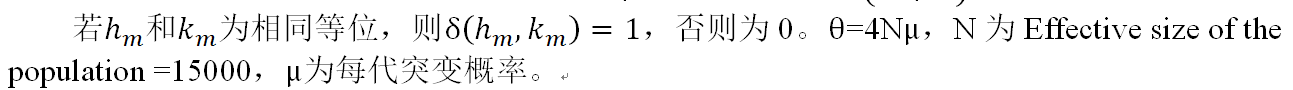
 　　抽样部分：

　　对于一个无关个体，设G和D分别观测的基因型和未知的二倍体。目标就是求出P(D|G,h_g)。

　　对于给定的G，如果G中含有s个杂合子位点，则所有单体型的个数为2^s，当SNP个数增大时，该数量不可计算。所以使用类似压缩图的方法对其进行压缩，形成s_g。通常s_g 每个片段包含3个杂合位点。每个单体在s_g中都有唯一路径x={x₁,..,x_m,...,x_M}。

　　与图H_g相比，有s_g两个不同，第一是片段的边界不同，第二是图s_g没有权重。

　　

 

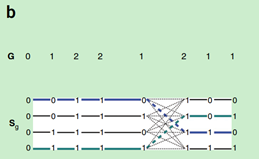
图3

　　P(D|G,h_g)即从P(h|h_g)中抽取中的一个路径h，也就相当于从P(x|h_g)中抽取一个路径x放入到s_g。即获得P(x|h_g)，其中x是s_g中的一个路径。

　　根据马尔科夫链特性，即当前节点仅与前一个节点有关，则在给定节点x_m时，x_m-1和x_m+1无关。所以有(这里有一个奇怪的特性，因为x是观测链，正常情况下x是不具有马尔科夫性的，但是这里却使用了马尔可夫性。这里可能是因为状态空间和观测空间是一致的，都是从{0,1}取值，所以也具有马尔可夫性，而且从文献可以看到在推测出观测链x之后，还有把x放入H进行下一个个体单体型的推测，这也要求其具有马尔可夫性)：

　　

　　这就构成了马尔可夫链，其中状态和转移分别为s_g中的点和边。从P(x₁|H_g)中随机抽取一个节点，然后使用P(x_m|x_m-1,H_g)进行迭代，直到完成M个节点的完整路径。

　　要计算P(x|H_g)即需要知道P(x₁|H_g)和P(x_m|x_m-1,H_g)。另外我们可以看到P(x|H_g)其实就是P(x,z|H_g)的一个边缘概率。P(x,z|H_g)是联合概率，它有两个边缘概率，分别是P(x|H_g)和P(z|H_g)。联合概率和边缘概率的关系为：

　　

 

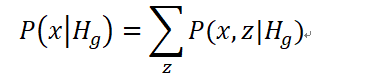
　　所以从解决边缘概率P(x|H_g)的问题转换为求联合概率P(x,z|H_g)。

　　对联合概率，有公式：

　　

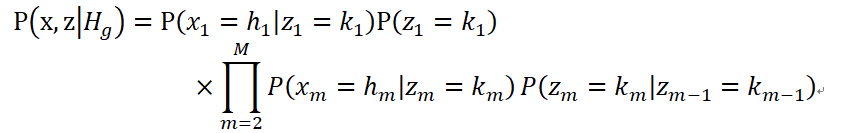
　　对于联合概率的求解，不是直接计算，而是采用前向后向的算法。

　　对于给定位置m，在m之前，使用前向算法：

　　

　　在给定位置m之后，使用后向算法：

　　

 

 

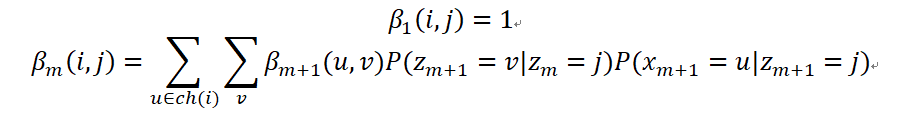
　　前向后向算法计算的是联合概率，所以最后使用联合概率的值计算边缘概率：

　　

 

 

 　　这里只获得了P(x1|Hg)和P(xm,xm+1|Hg)，并没有获得P(xm+1|x_m,H_g)，这里是一个吉布斯采样的过程，基于吉布斯采样有一个特性，即联合概率正比于条件概率：

　　　

　　此时就获得了条件概率P(x_m+1|x_m,H_g)的近似值，当获得这两项之后就可以使用一下公式，抽取符合基因型G的单体型了。

　　

 

 

 　　这样就可以计算每个x的概率。对于所有符合G的单体型对，选出概率最大的既可。每计算完一个个体，就把算出的结果放入H，重新构成一个新的隐马模型，然后对下一个个体进行计算，如此迭代，直到计算完成。

　　

　　SHAPEIT4更新内容：

　　SHAPEIT4更新了两个内容：1.更新H集合的构建方式；2.允许三种额外信息辅助分型。

　　

 

图4

　　1.更新H集合的构建方式

　　在SHAPEIT2中是从所有样本可能的单体型中随机选取K个构成集合H，然后对H进行压缩，基于压缩后的图构建模型。在SHAPEIT4中，在除了当前样本以外的所有样本可能的单体型上，使用PBWT算法，选出与当前样本可能单体型最相似的P个单体型构成集合H，然后按照每8个SNP一组，对H进行SHAPEIT2类似的压缩，然后建立模型。

 　　2.允许三种额外信息辅助分型

　　在SHAPEIT4可以使用三种额外信息来辅助进行SNP分析，这三种额外信息分别为：reference panel、haplotype scaffold和reads。使用这三种额外信息可以使分型结果更加准确。

　　其中S和R分别表示haplotype scaffold和reads提供的局部分型结果，reference panel的信息是在构建H时使用的，若存在reference panel，会在基于reference panel和其他样本的共同基础上建立PBWT算法，选出最相似的单体型，进而构建H。图5中S，即haplotype scaffold信息，在对图中Genotype graph构建的时候作为约束条件使用的。通过删除与haplotype scaffold不一致的候选h，可以减少Genotype graph的尺度。图5中的R，即reads信息，是在sampling的时候使用的，在进行sampling时，会允许选择的单体型h和reads信息有一定的错误率，并且通过选择的单体型h和reads信息进行比较，与reads信息越一致的单体型其权重越大，结果也更倾向于这样的单体型。根据以上描述，分别对reference panel、haplotype scaffold和reads信息进行利用，以辅助单体型分型。

 　　

 

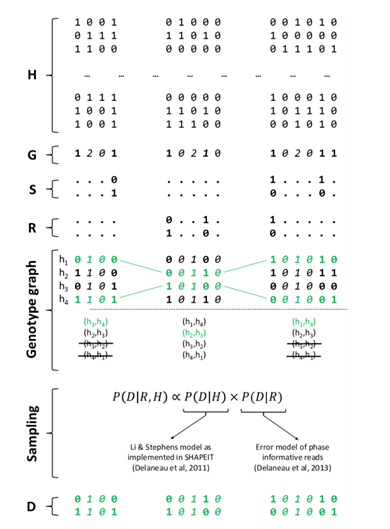
图5