【Note】(坑)一些组合恒等式的实际意义理解(和待填坑的组合数学知识)
- (1) \(C_n^m=C_n^{n-m}\)
- (2) \(A_n^m+mA_n^{m-1}=A_{n+1}^m\)
- (3) \(C_n^{m-1}+C_n^{m}=C_{n+1}^m \ or \ C_{n-1}^{m-1}+C_{n-1}^m=C_n^m\)
- (3*) \(\sum_{i=m}^nC_i^m=C_m^m+C_{m+1}^m+C_{m+2}^m+\cdots+C_{n-1}^m+C_n^m=C_{n+1}^{m+1}\)
- (4) \(C_n^{m-1}+2C_n^m+C_n^{m+1}=C_{n+2}^{m+1}\)
- (5) \(C_a^b \times C_b^c=C_a^c \times C_{a-c}^{b-c}=C_a^c \times C_{a-c}^{a-b}\)
- (6) \(\sum_{i=0}^{a}C_n^iC_m^{a-i}=C_n^0C_m^a+C_n^1C_m^{a-1}+\cdots+C_n^{a-1}C_m^1+C_n^aC_m^0=C_{n+m}^a\)
排列组合
恒等式
(1) \(C_n^m=C_n^{n-m}\)
从\(n\)个元素选择\(m\)个,等价于\(n\)个元素中不选\(n-m\)个。
(2) \(A_n^m+mA_n^{m-1}=A_{n+1}^m\)
在\(n+1\)个元素中选择\(m\)个元素排成一排,等价于考虑第\(n+1\)个元素:
- 不在该排列中:\(A_n^m\)
- 存在该排列中:\(mA_n^{m-1}\),\(m\)表示该元素有\(m\)种放置位置。
(3) \(C_n^{m-1}+C_n^{m}=C_{n+1}^m \ or \ C_{n-1}^{m-1}+C_{n-1}^m=C_n^m\)
在\(n+1\)个元素中选出\(m\)个元素,等价于考虑第\(n+1\)个元素:
- 不在该组合中:\(C_n^m\)
- 存在该组合中:\(C_n^{m-1}\)
(3*) \(\sum_{i=m}^nC_i^m=C_m^m+C_{m+1}^m+C_{m+2}^m+\cdots+C_{n-1}^m+C_n^m=C_{n+1}^{m+1}\)
可由式\((3)\)推导而出。
\(C_{m+1}^{m+1}=1=C_{m}^{m}\)
\(C_{m}^{m}+C_{m+1}^{m}=C_{m+1}^{m+1}+C_{m+1}^m=C_{m+2}^{m+1}\)
\(C_{m+2}^{m+1}+C_{m+2}^m=C_{m+3}^{m+1}\)
\(\cdots\)
\(C_{n}^{m+1}+C_n^m=C_{n+1}^{m+1}\)
得证。
事实上式\((3)\)可以认为是在杨辉三角上的递推。所以该式也可以由杨辉三角进行理解(如图)。
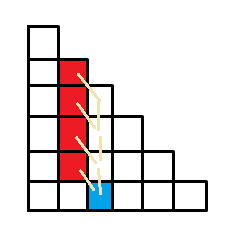
事实上很多恒等式都可以直接利用杨辉三角进行(眼睛上的)理解推导()
(4) \(C_n^{m-1}+2C_n^m+C_n^{m+1}=C_{n+2}^{m+1}\)
从\(n+2\)个元素中选出\(m+1\)个元素,考虑第\(n+1\)个元素和第\(n+2\)个元素:
- 两元素都不在该组合中:\(C_n^{m+1}\)
- 两元素都在该组合中:\(C_n^{m-1}\)
- 两元素有一个在该组合中:\(2C_n^m\)
(5) \(C_a^b \times C_b^c=C_a^c \times C_{a-c}^{b-c}=C_a^c \times C_{a-c}^{a-b}\)
考虑在集合\(A'\),\(|A'|=a\)中,求构造集合\(C' \subseteq B' \subseteq A'\),\(|C'|=c,|B'|=b\)的方案数。
- 先从\(A'\)中\(a\)个元素中取出\(b\)个元素放入\(B'\),再从\(B'\)中取出\(c\)个元素放入\(C'\):\(C_a^b \times C_b^c\)
- 先从\(A'\)中\(a\)个元素中取出\(c\)个元素放入\(C'\)(当然同时也放进了\(B '\)),再从剩下的\(a-c\)个元素中取出\(b-c\)个元素放入\(\complement_{B'}C'\)中:\(C_a^c \times C_{a-c}^{b-c}\)
(6) \(\sum_{i=0}^{a}C_n^iC_m^{a-i}=C_n^0C_m^a+C_n^1C_m^{a-1}+\cdots+C_n^{a-1}C_m^1+C_n^aC_m^0=C_{n+m}^a\)
在\(n+m\)个元素中选出\(a\)个元素:
- 前\(n\)个元素中选择了\(i\)个元素,后\(m\)个元素中选择了\(a-i\)个元素:\(C_n^iC_m^{a-i}\)
特别地,当\(m=n\)时:
\(\sum_{i=0}^aC_n^iC_n^{a-i}=C_{2n}^a\)
又根据\(C_n^i=C_n^{n-i}\),当\(a=n\)时:
\(\sum_{i=0}^n(C_n^i)^2=C_{2n}^n\)
多重集合(全)排列数
设可重集\(S=\{n_1 \cdot a_1,\cdots,n_k \cdot a_k \}\)
\(S\)的全排列数为:
$$\frac{n!}{n_1! \cdots n_k!}$$
将\(m\)个相同物品放入\(n\)个相同盒子 || 将正整数\(m\)划分成\(n\)个正整数的和
1.当作容量为\(n\),物品大小为\(1 \dots m\)的完全背包。
2.设\(f_{i,j}\)表示将正整数\(i\)划分为\(j\)个正整数之和的方案数:\(f_{i,j}=f_{i-1,j-1}+f_{i,j-i}\)
Catalan数
一些等价的Catalan数相关问题例:
- 入栈序列为\(1 \dots n\)的出栈序列种数;
- (基本模型)将\(n\)个\(0\)和\(n\)个\(1\)排成任意前缀\(0\)的个数不少于\(1\)的个数的序列数量;
- \(n\)个左括号和\(n\)个右括号组成的合法括号序列个数;
- \(n\)个节点构成的不同二叉树数量;
- 平面直角坐标系中从原点\((0,0)\)出发到\((2n,0)\),每一步可以向正右上或正右下移动,并且路径不经过第四象限的方案数
- \(\dots\)
使用例\((3)\)来说明,对\(n\)个节点构成二叉树数量的一种\((0)\)的理解:入栈后继续入栈为左儿子,直接出栈为没有左儿子;出栈后入栈为右儿子,直接出栈为没有右儿子。
其实这个问题的原本理解是:已知先序遍历,求构造中序遍历的方案数。
当然也可以理解为一个递推:设\(Cat_i\)表示\(i\)个节点构成二叉树的数量,那么有\(Cat_i=\sum_{j=0}^i Cat_j \times Cat_{i-j}\)
现在用例\((4)\)来说明:
平面直角坐标系中从原点\((0,0)\)出发到\((2n,0)\),每一步可以向正右上或正右下移动,并且路径不经过第四象限的方案数
也即有\(n\)个向右上的操作,\(n\)个向右下的操作。
可以考虑用所有的方案(\(C_{2n}^n\))减去不合法的(经过第四象限的方案)
每个不合法的方案必定经过直线\(y=-1\)。将这样每个方案第一个与该直线相交的点之后的整段路径,会得到唯一对应的一条终点为\((2n,-2)\)的路径。
也就是从\((0,0)\)到\((2n,-2)\)的每一条路径都对应了一条原问题不合法的路径。
所以答案即\(Cat_n=C_{2n}^n-C_{2n}^{n-1}\)
zzx:另外还有\(Cat_n=\frac{C^{n}_{2n}}{n+1}\)

