【模板复习+重构（重新开始）记录+注解】+【错误记录】

快速幂_取余

快速幂_取余运算

long long mod;
inline long long pow_(long long a,long long b)
{
	long long ans=1,base=a;
	while (b)
	{
		if (b&1)//拆解b的当前计算位
		{
			ans*=base;//（base是a的2的当前计算位-1次幂次幂）
			ans%=mod;
		}
		base*=base;//（base^2）
		base%=mod;
		b>>=1;
	}
	return ans;
}

int main()
{
	long long n,m;
	scanf("%lld%lld%lld",&n,&m,&mod);
	printf("%lld^%lld mod %lld=%lld\n",n,m,mod,pow_(n,m));
}

（tips：long tmd）

线段树_区间加

#define MAXN (int)(1e5+233) 
long long ans[MAXN<<2],tag[MAXN<<2];
int n,m;
#define leftson cur<<1
#define rightson cur<<1|1
#define mid ((l+r)>>1)
#define len (r-l+1)
#define push_up ans[cur]=ans[leftson]+ans[rightson]
#define push_down down(leftson,l,mid,tag[cur]); down(rightson,mid+1,r,tag[cur]); tag[cur]=0//其实这里似乎应该加一个if (tag[cur]!=0)（？）
void build(int cur,int l,int r)
{
	if (l==r)
	{
		scanf("%lld",&ans[cur]);
		return;
	}
	build(leftson,l,mid);
	build(rightson,mid+1,r);
	push_up;
}
inline void down(int cur,int l,int r,long long k)
{
	ans[cur]+=(len*k);
	tag[cur]+=k;
	return;
}
void add(int cur,int l,int r,int cl,int cr,long long k)
{
	if (cl<=l&&r<=cr)
	{
		ans[cur]+=(k*len);
		tag[cur]+=k;
		return;
	}
	push_down;//节点标记下传
	if (cl<=mid) add(leftson,l,mid,cl,cr,k);//修改区间包含左子树则操作
	if (cr>mid) add(rightson,mid+1,r,cl,cr,k);//修改区间包含右子树则操作
	push_up;//上传
}
long long query(int cur,int l,int r,int ql,int qr)
{
	if (ql<=l&&r<=qr) return ans[cur];
	push_down;
	long long answ=0;
	if (ql<=mid) answ+=query(leftson,l,mid,ql,qr);
	if (qr>mid) answ+=query(rightson,mid+1,r,ql,qr);
	push_up;
	return answ;
}
int main()
{
	scanf("%d%d",&n,&m);
	build(1,1,n);
	int opt,x,y;
	long long k;
	while(m--)
	{
		scanf("%d%d%d",&opt,&x,&y);
		if (opt==1)
		{
			scanf("%lld",&k);
			add(1,1,n,x,y,k);
		}
		else printf("%lld\n",query(1,1,n,x,y));
	}
	return 0;
}

>（tips：傻逼才会把len mid k写乱位置，我是傻逼）//QAQ 我也会（

（tips：n*m的数组for 1 to n for 1 to n 是傻逼）

线段树2_区间乘_区间加

更新了一份今年写的

线段树2_区间乘_区间加

#define MAXN (int)(1e5+233)
#define ll long long
ll mod;
struct tre
{
	ll ans,multag,addtag;
	int ls,rs;
	int l,r;
}a[MAXN<<2];/////////////////////////////////////////

#define ls a[cur].ls
#define rs a[cur].rs
#define l a[cur].l
#define r a[cur].r
#define mid ((l+r)>>1)
#define len (1ll*(r-l+1))
#define push_up a[cur].ans=(a[ls].ans+a[rs].ans)%mod;
#define push_down if (a[cur].multag!=1||a[cur].addtag!=0) { pushd(ls,a[cur].multag,a[cur].addtag); pushd(rs,a[cur].multag,a[cur].addtag); a[cur].multag=1; a[cur].addtag=0; }

inline void pushd(int cur,ll mulk,ll addk)
{
	a[cur].ans=a[cur].ans*mulk%mod;
	a[cur].ans=(a[cur].ans+addk*len%mod)%mod;
	a[cur].multag=a[cur].multag*mulk%mod; a[cur].addtag=(a[cur].addtag*mulk%mod+addk)%mod;
	return;
}

inline void build(int cur,int L,int R)
{
	a[cur].multag=1; a[cur].addtag=0;
	l=L; r=R;
	ls=cur<<1; rs=cur<<1|1;
	if (l==r) { scanf("%lld",&a[cur].ans); return; }
	build(ls,l,mid); build(rs,mid+1,r);
	push_up;
	return;
}

inline void add(int cur,int cl,int cr,ll k)
{
	if (cl<=l&&r<=cr)
	{
		a[cur].ans=(a[cur].ans+(k*len))%mod;
		a[cur].addtag+=k; a[cur].addtag%=mod;
		return;
	}
	push_down;
	if (cl<=mid) add(ls,cl,cr,k);
	if (cr>mid) add(rs,cl,cr,k);
	push_up;
	return;
}

inline void mul(int cur,int cl,int cr,ll k)
{
	if (cl<=l&&r<=cr)
	{
		a[cur].ans*=k; a[cur].ans%=mod;
		a[cur].addtag*=k; a[cur].addtag%=mod;
		a[cur].multag*=k; a[cur].multag%=mod;
		return;
	}
	push_down;
	if (cl<=mid) mul(ls,cl,cr,k);
	if (cr>mid) mul(rs,cl,cr,k);
	push_up;
	return;
}


inline ll query(int cur,int ql,int qr)
{
	if (ql<=l&&r<=qr) return a[cur].ans;
	push_down;
	ll ANS=0;
	if (ql<=mid) ANS=(ANS+query(ls,ql,qr))%mod;
	if (qr>mid) ANS=(ANS+query(rs,ql,qr))%mod;
	push_up;
	return ANS;
}

int n,q;

int main()
{
	scanf("%d%d%lld",&n,&q,&mod);
	build(1,1,n);
	int opt,x,y; ll k;
	while (q--)
	{
		scanf("%d%d%d",&opt,&x,&y);
		if (opt==1)
		{
			scanf("%lld",&k);
			mul(1,x,y,k);
		}
		else if (opt==2)
		{
			scanf("%lld",&k);
			add(1,x,y,k);
		}
		else
		{
			printf("%lld\n",query(1,x,y));
		}
	}
	return 0;
}

------------------

gcd

int gcd(int a,int b)
{
	if (b==0) return a;
	return gcd(b,a%b);
}
//lcm:a/gcd(a,b)*b;

------------------

树状数组_单点加_区间查询

附一个lowbit的意义：非负整数n在二进制表示下，最低位的1及后边所有的0构成的数值。例如$lowbit((1001100)_2)=(100)_2$。

树状数组_单点加_区间查询

#define MAXN (int)(5e5+233)
int n,m;
int c[MAXN];
#define lowbit(a) (a&-a)
inline void add(int x,int k)
{
	while (x<=n)
	{
		c[x]+=k;
		x+=lowbit(x);
	}
}
inline int query(int x)
{
	int sum=0;
	while (x>0)
	{
		sum+=c[x];
		x-=lowbit(x);
	}
	return sum;
}
inline int solve(int x,int y) { return query(y)-query(x-1); }//如果有进行模运算这里应该需要注意一下...

int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1,k;i<=n;i++)
	{
		scanf("%d",&k);
		add(i,k);
	}
	int opt,x,y;
	while (m--)
	{
		scanf("%d%d%d",&opt,&x,&y);
		if (opt==1) add(x,y);
		else printf("%d\n",solve(x,y));
	}
}

（tips：void return int的sb（）

（tips：减模小心爆负）

（tips：线段树开四倍数组（（

树链剖分

#define MAXN (int)(1e5+233)
struct qwq
{
	int nex,to;
}e[MAXN<<1];
int h[MAXN],tot=0;
int n,m,r;
long long mod;
inline void add(int x,int y)
{
	e[++tot].nex=h[x];
	e[tot].to=y;
	h[x]=tot;
}
long long a[MAXN],a2[MAXN];
//seg_tree
long long ans[MAXN<<2],tag[MAXN<<2];
#define leftson cur<<1
#define rightson cur<<1|1
#define mid ((l+r)>>1)
#define len (r-l+1)
#define push_up ans[cur]=ans[leftson]+ans[rightson]
#define push_down down(leftson,l,mid,tag[cur]); down(rightson,mid+1,r,tag[cur]); tag[cur]=0;
//线段树部分
inline void down(int cur,int l,int r,long long k)
{
	ans[cur]+=((len*k)%mod);
	tag[cur]+=k;
	ans[cur]%=mod;
	tag[cur]%=mod;
}
void build(int cur,int l,int r)
{
	if (l==r)
	{
		ans[cur]=a2[l];//建树使用新dfs序编号
		return;
	}
	build(leftson,l,mid);
	build(rightson,mid+1,r);
	push_up;
}
void change(int cur,int l,int r,int cl,int cr,long long k)
{
	if (cl<=l&&r<=cr)
	{
		ans[cur]+=((len*k)%mod);
		tag[cur]+=k;
		ans[cur]%=mod;
		tag[cur]%=mod;
		return;//main开头的调试甚至是因为这里没写return（）
	}
	push_down;
	if (cl<=mid) change(leftson,l,mid,cl,cr,k);
	if (cr>mid) change(rightson,mid+1,r,cl,cr,k);
	push_up;
}
long long query(int cur,int l,int r,int ql,int qr)
{
	if (ql<=l&&r<=qr) return ans[cur]%mod;
	push_down;
	long long answ=0;//不要和线段树数组重名!!!!!!!!!!!!!!!!!!!!!!!wtm错了好多次
	if (ql<=mid) answ+=query(leftson,l,mid,ql,qr)%mod;
	if (qr>mid) answ+=query(rightson,mid+1,r,ql,qr)%mod;
	push_up;
	return answ%mod;
}

//tree
int id[MAXN],son[MAXN],dep[MAXN],fa[MAXN],siz[MAXN],top[MAXN];//父亲，深度，子树大小，重儿子，重链顶，树剖dfs序编号
//init
void dfs_1(int x)
{
	siz[x]=1;//子树要先计算本身
	int maxn=-1;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (y==fa[x]) continue;
		fa[y]=x;
		dep[y]=dep[x]+1;
		dfs_1(y);
		siz[x]+=siz[y];//愿世间没有____=____+1
		if (siz[y]>maxn)//子树最大的儿子为重儿子
		{
			son[x]=y;
			maxn=siz[y];
		}
	}
}
int cnt=0;
void dfs_2(int x,int tp)
{
	id[x]=++cnt;
	a2[cnt]=a[x];
	top[x]=tp;//重链顶
	if (!son[x]) return;//重链由重儿子延续
	dfs_2(son[x],tp);
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (y==fa[x]||y==son[x]) continue;
		dfs_2(y,y);//轻儿子作为新重链顶
	}
}

//add list
inline void add_list(int x,int y,long long k)
{
	while (top[x]!=top[y])//当x，y不在同一条链上，进行跳链
	{
		if (dep[top[x]]<dep[top[y]]) swap(x,y);//更新为x相对y所在链顶端深度较低
		change(1,1,n,id[top[x]],id[x],k);//对x所在的链中被需操作链包含的部分操作，即当前x所在重链由x到重链顶 
		x=fa[top[x]];//x跳至当前重链顶
	}
	if (dep[x]>dep[y]) swap(x,y);
	change(1,1,n,id[x],id[y],k);//x与y在同一条链上，则编号连续，直接进行操作
	return;
}
//query list
inline long long query_list(int x,int y)
{
	long long answ=0;
	while (top[x]!=top[y])
	{
		if (dep[top[x]]<dep[top[y]]) swap(x,y);
		answ+=query(1,1,n,id[top[x]],id[x]);
		answ%=mod;
		x=fa[top[x]];
	}
	if (dep[x]>dep[y]) swap(x,y);
	answ+=query(1,1,n,id[x],id[y]);
	return answ%mod;
}
//add tree
inline void tree_add(int x,long long k)
{
	change(1,1,n,id[x],id[x]+siz[x]-1,k);//树链剖分所得的dfn本身是一种dfs序，子树由id[x]开始编号连续。
}
//query tree
inline long long tree_query(int x)
{
	return query(1,1,n,id[x],id[x]+siz[x]-1);
}
int main()
{
	scanf("%d%d%d%lld",&n,&m,&r,&mod);
	for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
	for (int i=1,x,y;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs_1(r);
	dfs_2(r,r);
	build(1,1,n);
	/*
	puts("uwu");
	for (int i=1;i<=n;i++) printf("%d ",id[i]);
	puts("w");*/
	int opt;
	int x,y;
	long long z;
	while (m--)
	{
		scanf("%d",&opt);
		if (opt==1)
		{
			scanf("%d%d%lld",&x,&y,&z);
			add_list(x,y,z);
		}
		else if (opt==2)
		{
			scanf("%d%d",&x,&y);
			printf("%lld\n",query_list(x,y));
		}
		else if (opt==3)
		{
			scanf("%d%lld",&x,&z);
			tree_add(x,z);
		}
		else
		{
			scanf("%d",&x);
			printf("%lld\n",tree_query(x));
		}
	}
	return 0;
}

单调队列

#define MAXN (int)(1e6+233)
#include <queue>
struct qwq
{
	int id,w;
};
int a[MAXN];
deque<qwq> q;
int main()
{
	int n,k;
	scanf("%d%d",&n,&k);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=1;i<=n;i++)//求长度为k窗口最小值，队列内元素单调递增
	{
		while (!q.empty()&&q.back().w>=a[i]) q.pop_back();//出现更小元素时，前面的小元素就过期（不可能再成为最小值）了，从队尾出队。
		q.push_back((qwq){i,a[i]});
		while (!q.empty()&&q.front().id<(i-k+1)) q.pop_front();//队列中元素出现时间单调递增，过期元素从队头出队
		if (i>=k) printf("%d ",q.front().w);
	}
	puts("");
	q.clear();
	for (int i=1;i<=n;i++)
	{
		while (!q.empty()&&q.back().w<=a[i]) q.pop_back();
		q.push_back((qwq){i,a[i]});
		while (!q.empty()&&q.front().id<(i-k+1)) q.pop_front();
		if (i>=k) printf("%d ",q.front().w);
	}
	return 0;
}

单调栈

#include <stack>
int n;
#define MAXN (int)(3e6+233)
stack<int> st;
int a[MAXN],r[MAXN];
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=1;i<=n;i++)
	{
		while (!st.empty()&&a[st.top()]<a[i])//求每个数右边第一个比其大的数的下标，栈内元素由底到顶单调递减。当入栈不满足单调性时持续出栈
		{
			r[st.top()]=i;//出栈过程即可标记
			st.pop();
		}
		st.push(i);
	}
	for (int i=1;i<=n;i++) printf("%d ",r[i]); puts("");
	return 0;
}

注意：使用dijkstra或者SPFA时，都要注意其中n，m的含义。并且此处给出的板子使用的是int，务必好好检查数据范围、数据类型、点数边数以及初始化。

dijkstra

#define MAXN 2510
#define MAXM 6200
int n,m,s,t;
#define inf (int)(1e9+300)
struct qwq
{
	int nex,to,w;//check long long
}e[MAXM<<1];
int h[MAXN],tot=0;
inline void add(int x,int y,int z)
{
	e[++tot].nex=h[x];
	e[tot].to=y;
	h[x]=tot;
	e[tot].w=z;
}

int vis[MAXN],dis[MAXN];

inline void dijkstra()
{
	int x=s;
	vis[x]=1;//设源点为已遍历
	dis[x]=0;//源点到本身最短路为0
	int summmm=n-1,minn=inf;
	while (summmm--)//执行n-1次
	{
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (dis[y]>dis[x]+e[i].w)
				dis[y]=dis[x]+e[i].w;
		}
		minn=inf;
		for (int i=1;i<=n;i++)
		{
			if (!vis[i]&&dis[i]<minn)//找出未遍历的未更新答案的节点
			{
				minn=dis[i];
				x=i;
			}
		}
		vis[x]=1;//将新的预遍历节点标记
	}
}

int main()
{
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for (int i=1,u,v,w;i<=m;i++)
	{
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		add(v,u,w);
	}
	for (int i=1;i<=n;i++) dis[i]=inf;
	dijkstra();
	printf("%d\n",dis[t]);
}

Dijkstra_priority_queue_optimized

#include <queue>
int n,m,s;
#define MAXN (int)(1e5+233)
#define MAXM (int)(2e5+233) 
struct qwq
{
	int nex,to,w;
}e[MAXM];
int h[MAXN],tot=0;
inline void add(int x,int y,int z)
{
	e[++tot].to=y;
	e[tot].w=z;
	e[tot].nex=h[x];
	h[x]=tot;
}
bool vis[MAXN];
int dis[MAXN];
struct Node { int id,diss; };
bool operator < (const Node &a,const Node &b) { return a.diss>b.diss; }
priority_queue<Node> q;
inline void dijkstra()
{
	int x;
	q.push((Node){s,0});//先把起点塞进优先队列里
	dis[s]=0;
	while (!q.empty())
	{
		x=q.top().id; q.pop();
		if (vis[x]) continue;//访问过了就跳过。
		vis[x]=true;//check in！
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (dis[y]>dis[x]+e[i].w)
			{
				dis[y]=dis[x]+e[i].w;//更新
				if (!vis[y])
					q.push((Node){y,dis[y]});//未访问过就塞进去
			}
		}
	}
}

int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for (int i=1,x,y,z;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
	}
	for (int i=1;i<=n;i++) dis[i]=(int)(2e9+7000);
	dijkstra();
	for (int i=1;i<=n;i++) printf("%d ",dis[i]);
	return 0;
}

（tips：stl的priority_queue默认是大根堆。写转义运算符的时候要把符号反过来）

（tips：以及....初始化dis。）

缩点

yysy，这里好像有个点双边双连通分量板子....

https://www.luogu.com.cn/team/21355#problem

无向图缩点

#define MAXN (int)(1e4+233)
#define MAXM (int)(1e5+233)
#include <stack>
int a[MAXN];
stack<int> st;
struct qwq
{
	int nex,to;
}e[MAXM],e2[MAXM];
int h[MAXN],h2[MAXN],tot=0,tot2=0;
inline void add(int x,int y)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	h[x]=tot;
}
bool vis[MAXN];
int dfn[MAXN],lst[MAXN],cnt=0;
int color[MAXN],c_count=0;
int w[MAXN];
void tarjan(int x)
{
	vis[x]=true;//vis实际上表示该节点是否在栈中，此处标记x入栈 
	st.push(x);//x入栈 
	dfn[x]=lst[x]=++cnt;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (!dfn[y]) { tarjan(y); lst[x]=min(lst[x],lst[y]); }//y未遍历过，(x,y)为树枝边 
		else if (vis[y]) lst[x]=min(lst[x],dfn[y]);//y在栈内 
	}
	if (dfn[x]==lst[x])//x为x所在的连通分量的根 
	{
		color[x]=++c_count;//对x染色 
		vis[x]=false;//出栈标记 
		w[c_count]+=a[x];//统计分量点权值和 
		int y;
		while (st.top()!=x)
		{
			y=st.top();
			color[y]=c_count;//对连通分量中的点染色 
			vis[y]=false;//出栈标记 
			w[c_count]+=a[y];//统计分量点权值和 
			st.pop();
		}
		st.pop();
	}
}
int in[MAXN];
inline void add2(int x,int y)
{
	in[y]++;
	e2[++tot2].to=y;
	e2[tot2].nex=h2[x];
	h2[x]=tot2; 
}
#include <queue>
queue<int> q;
int f[MAXN];
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=1,x,y;i<=m;i++) scanf("%d%d",&x,&y),add(x,y);
	for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i);
	for (int x=1;x<=n;x++)
		for (int i=h[x];i;i=e[i].nex) 
			if (color[x]!=color[e[i].to]) add2(color[x],color[e[i].to]);//以连通分量为单位重新建图（记得写add2） 
	//从这里开始使用图e2[] 
	for (int i=1;i<=c_count;i++)//新图节点数是c_count 
	{
		if (!in[i]) q.push(i);
		f[i]=w[i];
	}
	int x; 
	while (!q.empty())//缩点后图形态为DAG。进行DAG上的最长路DP 
	{
		x=q.front();
		q.pop();
		for (int i=h2[x],y;i;i=e2[i].nex)
		{
			y=e2[i].to;
			in[y]--;
			f[y]=max(f[y],f[x]+w[y]);
			if (!in[y]) q.push(y);
		}
	}
	int ans=-1;
	for (int i=1;i<=n;i++) ans=max(ans,f[i]);
	printf("%d\n",ans);
	return 0;
}

https://www.luogu.com.cn/record/59925909

无向图上求双连通分量，先求出桥并标记再dfs染色。

这个代码是模拟赛时的，桥的判定是lst[y]>dfn[x]

边编号从2开始，相同边的反向边由异或1互相转换。

无向图边双联通分量缩点

边双缩点

#define MAXN (int)(5e4+233)
#define MAXM (int)(5e4+233)
struct qwq
{
	int nex,to;
}e[MAXM<<1];
int h[MAXN],tot=1;
int n,m;
inline void add(int x,int y)
{
	e[++tot].nex=h[x];
	e[tot].to=y;
	h[x]=tot;
}
bool book[MAXM<<1];
int dfn[MAXN],lst[MAXN],cnt=0;
void tarjan(int x,int ie)
{
	dfn[x]=lst[x]=++cnt;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (!dfn[y])
		{
			tarjan(y,i);
			lst[x]=min(lst[x],lst[y]);
			if (lst[y]>dfn[x]) book[i]=book[i^1]=true;//,printf("bridge: %d %d\n",x,y);
		}
		else if (i!=(ie^1)) lst[x]=min(lst[x],dfn[y]);//不等于从父亲来的那条边。这样写可以处理重边
	}
}
int color[MAXN],c_count=0;
void dfs(int x)
{
	color[x]=c_count;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (color[y]||book[i]) continue;
		dfs(y);
	}
}
int deg[MAXN];
inline int tc(int x)
{
	if (x%2==0) return x/2;
	return (int)(x*1.0/2.0)+1;
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i,0);
	for (int i=1;i<=n;i++)
		if (!color[i]) { c_count++; dfs(i); }
	for (int x=1;x<=n;x++)
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (color[x]!=color[y])
				deg[color[y]]++;
		}
	int sum=0;
	for (int i=1;i<=c_count;i++)
		if (deg[i]==1) sum++;
	printf("%d\n",tc(sum));
	return 0;
}

割点

#define MAXN (int)(2e4+233)
#define MAXM (int)(1e5+233)
struct qwq
{
	int nex,to;
}e[MAXM<<1];
int h[MAXN],tot=0;
inline void add(int x,int y)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	h[x]=tot;
}
int dfn[MAXN],lst[MAXN];
int id=0;
bool cut[MAXN];
int rt;
void tarjan(int x)
{
	dfn[x]=lst[x]=++id;
	int ssum=0;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (!dfn[y])
		{
			tarjan(y);
			lst[x]=min(lst[x],lst[y]);
			if (lst[y]>=dfn[x]&&x!=rt) cut[x]=true;//割点判定
			ssum++;
		}
		else lst[x]=min(lst[x],dfn[y]);
	}
	if (x==rt&&ssum>1) cut[rt]=true;//当前搜索树的root，须有至少两个子节点y满足lst[y]>=dfn[x]才为割点
}
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	for (int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	} 
	for (int i=1;i<=n;i++)
		if (!dfn[i]) { rt=i; tarjan(i);  }
	int sum=0;
	for (int i=1;i<=n;i++)
		if (cut[i]) sum++;
	printf("%d\n",sum);
	for (int i=1;i<=n;i++)
		if (cut[i]) printf("%d ",i); puts("");
	return 0;
}

写了个假的v-DCC做法之后发现一个很大的误区

v-DCC的含义是极大不含割点的子图。一个割点可能被多个v-DCC包含

一张无向图是点双连通图，当且仅当满足下列两个条件之一

1.图的顶点数不超过2

2.图中任意两点都同时包含在至少一个简单环中。（属于两个不同点双连通分量的两个节点，不可能同时包含在至少一个简单环中）

书中其实还有个引理（）若某个v-DCC中存在奇环，则这个v-DCC中的所有点都被至少一个奇环包含。很好证，不写了（

求点双过程写代码注释里了（

点双连通分量

#define MAXN (int)(5e4+233)
#define MAXM (int)(1e5+233)
int n,m;
struct qwq
{
	int nex,to;
}e[MAXM<<1];
int h[MAXN],tot=0;
inline void add(int x,int y)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	h[x]=tot;
}
#include <stack>
#include <vector>
stack<int> st;
int dfn[MAXN],lst[MAXN],cnt=0;
bool Cut[MAXN];
int rt;
vector<int> v[MAXN];
int vcnt=0;
void Tarjan(int x)
{
	dfn[x]=lst[x]=++cnt;
	st.push(x);//1.当一个节点第一次被访问，将该节点入栈。
	int ssum=0;
	if (x==rt&&(!h[x])) { v[++vcnt].push_back(x); return; }
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (!dfn[y])
		{
			Tarjan(y);
			lst[x]=min(lst[x],lst[y]);
			if (lst[y]>=dfn[x])//2.当割点判定成立（x为割点时）
			{
				if (x!=rt)
					Cut[x]=true;//这里还顺便求了割点来着....似乎是不用求的（？
				else
					ssum++;
				//从栈顶不断弹出节点直至y被弹出
				int z;
				vcnt++;
				do
				{
					z=st.top();
					st.pop();
					v[vcnt].push_back(z);
				} while (z!=y);
				v[vcnt].push_back(x);//刚刚弹出的所有节点与x一起构成了一个v-DDC。
			}
		}
		else lst[x]=min(lst[x],dfn[y]);
	}
	if (x==rt&&ssum>=2) Cut[x]=true;
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	for (int i=1;i<=n;i++)
		if (!dfn[i])
		{
			rt=i;
			Tarjan(i);
		}
//	for (int i=1;i<=n;i++) printf("%d ",Cut[i]); puts("w");
	for (int i=1,len;i<=vcnt;i++)
	{
		len=v[i].size();
		for (int j=0;j<len;j++)
			printf("%d ",v[i][j]);
		printf("\n");
	}
	return 0;
}

然后就是点双缩点了

方法是先给每个割点新标一个号，再将每个v-DDC与它包含的所有割点连边。

代码暂时没有（）

二分

1.整数区间上二分

(I)查找最小的答案

Code

inline void binary_search(int l,int r)
{
	#define mid ((l+r)>>1)
	while (l<r)
		if (check(mid))
			r=mid;
		else l=mid+1;
	return l;
}

(II)查找最大的答案

Code

inline void binary_search(int l,int r)
{
	#define mid ((l+r+1)>>1)
	while (l<r)
		if (check(mid))
			l=mid;
		else r=mid-1;
	return l;
}

(III)实数域二分

Code

while (l+eps<r)
{
	double mid=(l+r)/2;
	if (check(mid)) r=mid; else l=mid;
}

其中eps为精度。若要保留k位小数，则取$eps=10^{-(k+2)}$

乘法逆元

差点忘了。

$a\div b \ mod \ p = a*b^{p-2} \ mod \ p$

线性求逆元

#define MAXN (int)(3e6+233) 
int n;
long long mod;
long long inv[MAXN]; 

int main()
{
	scanf("%d%lld",&n,&mod);
	inv[1]=1;
	for (int i=2;i<=n;i++)
		inv[i]=(mod-mod/i)*inv[mod%i]%mod;
	for (int i=1;i<=n;i++)
		printf("%lld\n",inv[i]);
	return 0;
}

阶乘求逆元

先求出inv[n!]。然后inv[i!]=inv[(i+1)!]*(i+1)

嗯....似乎还要复习一下基本的dp什么的。相当生疏了啊

二分图判定

.....怎么会有这个东西。。。。。。。。。。。。。。。

一张无向图是二分图，当且仅当图中不存在长度为奇数的环。

黑白染色即可。一个节点的相邻节点应与其染色相反，若染色过程产生冲突，则存在奇环。

所以反过来二分图判定也可以用来判奇环（）

（tips：注意题目是否给出树根）

（tips：longlong！！！！！！！！longlong！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！）

（tips：出现一个非0数到了另一个地方变成0了，可能是因为int a=(long long)了）

SPFA求负环

SPFA

//再强调一次：一定要注意计算点数、边数，检查初始化。
#include <queue>
#define ll long long
const ll inf=(ll)(1e16);
#define MAXN (int)(2e3+233)
#define MAXM (int)(6e3+233)
struct qwq
{
	int nex,to;
	ll w;
}e[MAXM];//注意算边数（以及考虑双向边）
int h[MAXN],tot=0;
int n,m;
inline void add(int x,int y,ll z)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	e[tot].w=z;
	h[x]=tot;
}
ll dis[MAXN];
int cnt[MAXN];
bool vis[MAXN];
queue<int> q;
inline void INIT()
{
	for (int i=1;i<=maxnode;i++) h[i]=0,dis[i]=inf,cnt[i]=0,vis[i]=false; tot=0;//注意点数
	while (!q.empty()) q.pop();
	return;
}

inline bool spfa(int s)
{
	dis[s]=0; q.push(s); vis[s]=true;
	int x;
	while (!q.empty())
	{
		x=q.front(); q.pop(); vis[x]=false;
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (dis[y]>dis[x]+e[i].w)
			{
				dis[y]=dis[x]+e[i].w;
				if (!vis[y])
				{
					cnt[y]++;
					if (cnt[y]>=maxnode) return false;//注意点数视情况修改
					q.push(y); vis[y]=true;
				}
			}
		}
	}
	return true;
}
//bellman_ford，可以判断从s到t的路径上是否有负环。具体操作是再进行maxnode轮松弛，判断dis[t]有没有变小即可。
//bellman_ford第i松弛计算出的dis数组表示：从s出发至多i步到达t的最短路
inline bool bellman_ford(int s)
{
	dis[s]=0;
	for (int k=1;k<maxnode;k++)
		for (int x=1;x<=maxnode;x++)
		{
			if (dis[x]==inf) continue;
			for (int i=h[x],y;i;i=e[i].nex)
			{
				y=e[i].to;
				if (dis[y]>dis[x]+e[i].w)
					dis[y]=dis[x]+e[i].w;
			}
		}
	for (int x=1;x<=maxnode;x++)
	{
		if (dis[x]==inf) continue;
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (dis[y]>dis[x]+e[i].w) return false;//可以继续松弛，则有负环
		}
	}
	return true;
}

inline void R()
{
	scanf("%d%d",&n,&m);
	INIT();
	for (int i=1,x,y;i<=m;i++)
	{
		ll z;
		scanf("%d%d%lld",&x,&y,&z);
		if (z>=0) add(x,y,z),add(y,x,z);
		else add(x,y,z);
	}
	// puts(spfa(1)?"NO":"YES");
	// for (int i=1;i<=n;i++) printf("%lld ",dis[i]); puts("");
	// puts(bellman_ford(1)?"NO":"YES");
	return;
}

int main()
{
	int T;
	scanf("%d",&T);
	while (T--) R();
	return 0;
}

（tips：多测要清空....queue？）

（tips：喂！！！！怎么能(int)(1e16)）

（tips：爆负了就从头到尾检查取模啊！！！！！！！！）

（tips：认真检查删调试！！）

（tips：别tm忘打大括号啊！！！！！！！！！）

（tips:l o n g l o n g ！！！！！！！！！！！！！！！！！！！！！！下次能开就开算了（）但是按照自己的做事方式似乎很难允许自己这么干）

带权并查集

在并查集的基础上对节点到父亲的边加了边权...... 路径压缩的时候就直接计算节点到根的边权和。

并查集还是带权并查集也好，都维护具有传递性的关系

放个例题：[ARC090B] People on a Line

给定$m$组信息，第$i$组信息形如$(l_i,r_i,d_i)$，含义为$x_{r_i}-x_{l_i}=d_i$。判断是否所有信息都不冲突

这题原题面花里胡哨的，其实跟另一个带权并查集板子是一样的（）那题是给出一系列区间和判断是否有冲突，实质上也是给出一组$a_{r_i}-a_{l_i}=d_i$

对于通过添加$root_r$到$root_l$关系的话，我画了个图（）虽然感觉有点冗余

这里用$fr$表示$root_r$，$fl$表示$root_l$

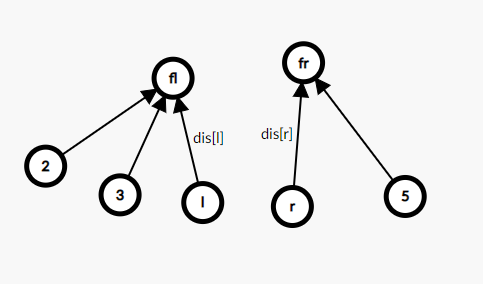
原先的情况

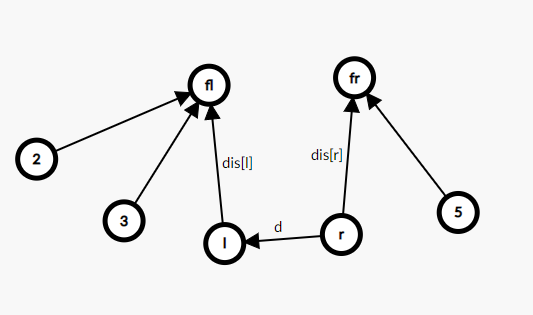
现在要建立一个r到l的关系d

怎么通过dis'[fr]来建立？

使得dis[l]+d=dis[r]+dis'[fr]，也即dis'[fr]=dis[l]+d-dis[r]

没了（

带权并查集

#define MAXN (int)(1e5+233)
int n,m;
int dis[MAXN],fa[MAXN];
inline void INIT() { for (int i=1;i<=n;i++) fa[i]=i; }
int found(int x)
{
	if (x==fa[x]) return x;
	int rt=found(fa[x]);//先找root
	dis[x]+=dis[fa[x]];//再更新在当前root下的前缀和。本来在想这么写为什么正确，然后发现并查集每次合并并且运行found后森林一直是一堆菊花图的形态
	return fa[x]=rt;//路径压缩
}

int main()
{
	scanf("%d%d",&n,&m);
	INIT();
	for (int i=1,l,r,d,fl,fr;i<=m;i++)
	{
		scanf("%d%d%d",&l,&r,&d);
		fl=found(l); fr=found(r);
//		for (int j=1;j<=n;j++) printf("%d %d\n",fa[j],dis[j]); puts("fA!");
		if (fl!=fr)
		{
			dis[fr]=d+dis[l]-dis[r];
			fa[fr]=fl;
		}
		else if (dis[r]-dis[l]!=d)//fl==fr，l与r在同个并查集中，也即l与r已经存在了联系。dis[i]表示r在[root[i]~i]区间的前缀和，即dis[r]-dis[l]可以表示l，r已经存在的这组联系值（换到区间和和那题更好表述为l+1到r的区间和）。
		{
			puts("No");
			return 0;
		}
	}
	puts("Yes");
	return 0;
}

https://www.luogu.com.cn/blog/wey-yzyl/zui-tai-zi-duan-hu-ji-ji-bian-shi-di-qi-shi

chy分享给我们的最大子段和变式及解法整理（）

（tips：线段树维护RMQ什么的...push_up记得写手写long long max/min函数啊）

（tips：别手瓢就tm(int)(1e18)啊！！！就算写#define mod (long long)(1e9+7)也还是别int...）

李超树

把 [HEOI2013] Segment 当板子写了

本来在想先写哪道（）Segment 是加线段，好像那道 JSOI 的是加直线，并且直线斜率大于0..

最后两个都写了。yysy，题解的码风各异....花了好多时间大致统一出了一个比较好看的写法。

[HEOI2013] Segment

#define MAXN (int)(1e5+233)
#define MAXXK (39989)
#define MAXK (int)(4e4+233)
#define MAXY (int)(1e9+233)
const double EPS=1e-8;
using namespace std;
int OPT;

struct Seg
{
	int l,r;
	int id;
	double k,b;
};
int countt=0;

#define leftson cur<<1
#define rightson cur<<1|1
#define mid ((l+r)>>1)
Seg ans[MAXK<<2];
int rn=(int)(4e4);

inline double cal(Seg i,int x) { return i.k*x+i.b; }

Seg query(int cur,int l,int r,int qs)
{
	if (l==r) return ans[cur];
	Seg answ;
	if (qs<=mid)
		answ=query(leftson,l,mid,qs);
	else
		answ=query(rightson,mid+1,r,qs);
	return cal(answ,qs)-cal(ans[cur],qs)>EPS?answ:ans[cur]; 
}
void change(int cur,int l,int r,Seg k)
{
	if (k.l<=l&&r<=k.r)//线段完全覆盖才更新 
	{
		if (!ans[cur].id) { ans[cur]=k; return; }
		if (cal(k,mid)-cal(ans[cur],mid)>EPS) swap(ans[cur],k);//优势判断 
		if (cal(k,l)-cal(ans[cur],l)>EPS) change(leftson,l,mid,k);//优势线段右侧完全优先，用劣势更新左子树 
		if (cal(k,r)-cal(ans[cur],r)>EPS) change(rightson,mid+1,r,k);//优势线段左侧完全优先，用劣势更新右子树 
		return;
	}
	if (k.l<=mid) change(leftson,l,mid,k);
	if (k.r>mid) change(rightson,mid+1,r,k);
}
int main()
{
	scanf("%d",&OPT);
	int lastans=0,opt;
	int K,xx0,yy0,xx1,yy1;
	while (OPT--)
	{
		scanf("%d",&opt);
		if (!opt)
		{
			scanf("%d",&K);
			K=(K+lastans-1)%39989+1;
			printf("%d\n",lastans=query(1,1,rn,K).id);
		}
		else
		{
			scanf("%d%d%d%d",&xx0,&yy0,&xx1,&yy1);
			xx0=(xx0+lastans-1)%39989+1;
			yy0=(yy0+lastans-1)%(int)(1e9)+1;
			xx1=(xx1+lastans-1)%39989+1;
			yy1=(yy1+lastans-1)%(int)(1e9)+1;
			if (xx0>xx1) swap(xx0,xx1),swap(yy0,yy1);
			countt++;
			Seg k=(Seg){xx0,xx1,countt,0,0};
			if (xx0==xx1) k.b=max(yy0,yy1);//垂直于x轴的线段 
			else k.k=((double)(yy1-yy0))/((double)(xx1-xx0)),k.b=(double)yy0-k.k*xx0;
			change(1,1,rn,k);
		}
	}
	return 0;
}

[JSOI2008] Blue Mary 开公司

#define MAXN (int)(1e5+233)
#define MAXT (int)(5e4+233)
const double EPS=1e-8;
const int rn=(int)(5e4);
using namespace std;
int tot=0;

int n;
struct Lin
{
	double k,b;
}a,ans[MAXT<<2];
inline double cal(Lin i,int x) { return i.k*x+i.b; }
#define leftson cur<<1
#define rightson cur<<1|1
#define mid ((l+r)>>1)
void change(int cur,int l,int r,Lin k)
{
	if (l==r)
	{
		if (cal(ans[cur],l)<cal(k,l)) ans[cur]=k;
		return;
	}
	if (!ans[cur].k) { ans[cur]=k; return; }
	if (cal(k,mid)-cal(ans[cur],mid)>EPS) swap(ans[cur],k);
	if (cal(k,l)-cal(ans[cur],l)>EPS) change(leftson,l,mid,k);
	if (cal(k,r)-cal(ans[cur],r)>EPS) change(rightson,mid+1,r,k);
}
double query(int cur,int l,int r,int qs)
{
	if (l==r) return cal(ans[cur],l);
	double answ=cal(ans[cur],qs);
	if (qs<=mid)
		answ=max(answ,query(leftson,l,mid,qs));
	else
		answ=max(answ,query(rightson,mid+1,r,qs));
	return answ; 
}
int main()
{
	scanf("%d",&n);
	string opt;
	int K;
	for (int i=1;i<=n;i++)
	{
		cin>>opt;
		if (opt[0]=='Q')
		{
			scanf("%d",&K);
			if (tot==0) printf("0\n");
			else printf("%d\n",(int)(query(1,1,rn,K)/100));
//			else printf("%lf\n",(query(1,1,rn,K)/*100*/));
		}
		else
		{
			tot++;
			scanf("%lf%lf",&a.b,&a.k); a.b-=a.k;
			change(1,1,rn,a);
		}
	}
	return 0;
}

（tips：别for j to k 该opt j 还 operate i 了（）

01分数规划

模型：给定一系列整数$a_1,a_2,...,a_n$与$b_1,b_2,...,b_n$，求解一组$x_i$$\space (1 \leq i \leq n , x_i = 0 \space or \space 1)$使得下式值最大化

\[\frac{\Sigma_{i=1}^{n}a_i*x_i}{\Sigma_{i=1}^{n}b_i*x_i} \]

解法：二分答案。把柿子拆一下

\[\frac{\sum_{i=1}^{n}a_i*x_i}{\sum_{i=1}^{n}b_i*x_i}\geq mid \]

\[\sum_{i=1}^{n}a_i \times x_i-mid \times (\sum_{i=1}^{n}b_i \times x_i) \geq 0 \]

\[\sum_{i=1}^{n}(a_i-mid \times b_i) \times x_i \geq 0 \]

那么就可以判断，若$a_i-mid*b_i < 0$，就令$x_i=0$，否则令$x_i=1$。

（tips：const double EPS!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1）

（tips：沃日，写到个SPFA判负环结果边权柿子是浮点数，int dis[]一发100 -> 30）

set/multiset

暂时没写总结啥的，先放个别人博客

除此还差bitset，list，平板电视之类的没学（

放个自己 AtCoder Beginner Contest 170 E - Smart Infants 的代码，在里面写使用注释算了（

AtCoder Beginner Contest 170 E - Smart Infants

#include <set>
#define MAXN (int)(2e5+233)
#define MAXQ (int)(2e5+233)
using namespace std;
int n,q;
int S[MAXN],a[MAXN];
multiset<int> st[MAXN],setans;

int main()
{
	scanf("%d%d",&n,&q);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i],&S[i]);
		st[S[i]].insert(a[i]);
	}
	for (int i=1;i<=(int)(2e5);i++)
		if (!st[i].empty()) setans.insert(*(--st[i].end()));//--st[i].end()，返回set st[i]末尾位置迭代器。set.end()是末尾+1。加星号是取了值（
	int c,d;
	while (q--)
	{
		scanf("%d%d",&c,&d);
		setans.erase(setans.find( *(--st[S[c]].end()) ));//find(x)，找到元素x所在位置的迭代器。在multiset中，multiset.erase(x)会导致将所有值为x的元素删除，而erase(it)就删除迭代器it所在的元素。
		if (!st[d].empty()) setans.erase(setans.find(*(--st[d].end())));
		st[S[c]].erase(st[S[c]].find(a[c]));
		st[d].insert(a[c]);//set.insert(x)，插入一个元素x。
		if (!st[S[c]].empty()) setans.insert(*(--st[S[c]].end()));
		setans.insert(*(--st[d].end()));
		printf("%d\n",*setans.begin());
		S[c]=d;
		//还有两个没写进去的（）这里记录一下吧
		//set.lower_bound(x) 在set中查找最小的*a>=x
		//set.upper_bound(x) 在set中查找最小的*a>x
	}
	return 0;
}

迭代器的使用

set<int>::iterator it;
for(set<int>::iterator it=s.begin();it!=s.end();it++) {}//遍历set中的元素（*it），其中it++的复杂度为log2n

草，一个很奇怪的点（）记得上考场前把校章摘下来QAQ————————————————————————————————————————————————————————————————————————————————————

（tips：多个dfs里要看清楚套哪个dfs函数.....）

（tips：清醒一点，和快一点。）

（tips：SPFA入队记得写标记..怎么会忘了这种事情。）

（tips：DP要想好最后要输出什么....某些状态中的最大，还是某个特定的状态？）

（tips：还要想好最后输出要不要模...）

线性筛素数

bitset埃筛

#include <bitset>
int P[(int)(1e7+233)],tot=0;
bitset<100000007> isp;
int main()
{
	int n,q;
	scanf("%d%d",&n,&q);
	isp.set();
	isp[0]=isp[1]=0;
	for (int i=2;i<=n;i++)
		if (isp[i]) 
		{
			P[++tot]=i;
			for (int j=(i<<1);j<=n;j+=i)
				isp[j]=0;
		}
	int k;
	while (q--)
	{
		scanf("%d",&k);
		printf("%d\n",P[k]);
	}
	return 0;
}

欧拉筛

int n,q;
#define MAXN (int)(1e8+233)
#define MAXQ (int)(1e6+233)
int p[(int)(1e7+233)],tot=0;
bool pri[MAXN];

inline void op()
{
	for (int i=2;i<=n;i++) pri[i]=true;
	for (int i=2;i<=n;i++)
	{//if (i==10) puts("10"); else if (i==10000) puts("10000"); else if (i==10000000) puts("10000000"); else if (i==n) puts("100000000");
		if (pri[i]) p[++tot]=i;
		for (int j=1;p[j]*i<=n&&j<=tot;j++)
		{
			pri[p[j]*i]=false;
			if (!(i%p[j])) break;
		}
	}
}

int main()
{
	scanf("%d%d",&n,&q);
	op();// puts("QAQ");
	int k;
	while (q--)
	{
		scanf("%d",&k);
		printf("%d\n",p[k]);
	}
	return 0;
}

（tips：开状压数组的时候1<<MAXN不要写成MAXN*2（MAXN<<1）那个...）

（tips：好好算数组空间。考场血の教训。话说用算别的运行空间吗？）

（tips：看好是n还是m还是k还是q还是i还是j还是你妈（）

（tips：记好不要写错continue/return/break。记好不要写int类型函数没有return。）

（tips：写inline别忘写函数类型啊！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！（要么干脆戒inline））

组合数问题模板

虽然到现在了应该不需要模板为好

存一下好了（）毕竟优化过的这种写法我只写过一次..

拿了个之前写过的题

#define MAXN (int)(1e7+233)
int n,k,r;
const long long mod=1e9+7;
inline long long power(long long A,long long B)
{
	long long Ans=1,base=A;
	while (B)
	{
		if (B&1) Ans=Ans*base%mod;
		base=base*base%mod; B>>=1;
	}
	return Ans;
}
int fac[MAXN],facv[MAXN];
inline void INIT()
{
	fac[0]=1;
	for (int i=1;i<=1e7;i++) fac[i]=fac[i-1]*1ll*i%mod;
	facv[(int)(1e7)]=power(fac[(int)(1e7)],mod-2);
	for (int i=1e7-1;i>=0;i--) facv[i]=facv[i+1]*1ll*(i+1)%mod;
}
inline long long C(int X,int Y) { if (X<Y) return 0; return ((fac[X]*1ll*facv[X-Y]%mod)*1ll*facv[Y])%mod; }

int main()
{
//	freopen("star.in","r",stdin);
//	freopen("star.out","w",stdout);
	scanf("%d%d%d",&n,&k,&r);
	INIT();
	if (r==1)
	{
		printf("%lld\n",C(n,k));
		return 0;
	}
	long long ans=0;
	for (int i=1;i<=k/r;i++) ans=(ans+((i&1)?1:-1)*1ll*((C(n-k+1,i))%mod*C(n-i*r,n-k)*1ll%mod)+mod)%mod;//c,又魔怔sb了,QAQ,样例好弱,我好蠢 
	printf("%lld\n",ans);
	return 0;
}

fhq_treap

fhq_Treap普通平衡树（插入，删除，查询值对应排名，查询排名对应值，查询前驱，查询后继）

#define MAXN (int)(1e5+233)
unsigned int SEED=1037;
inline unsigned int k_random() { return SEED=(unsigned int)(SEED*19260817%2147483647); }

struct Node
{
	int w,l,r,siz,pri;//权值，左儿子，右儿子，子树大小，键值 
}ans[MAXN];
int tot=0,Root=0;//点标号，树根 
#define leftson ans[cur].l
#define rightson ans[cur].r
#define push_up(CUR) ans[CUR].siz=ans[ans[CUR].l].siz+ans[ans[CUR].r].siz+1;//上传 uwu

inline int k_create(int W)//建点（没有写回收站） 
{
	ans[++tot].w=W;
	ans[tot].l=ans[tot].r=0;
	ans[tot].siz=1;
	ans[tot].pri=k_random();
	return tot;
}

void k_split_weight(int cur,int W,int &x,int &y)//按权值分裂。按<=W和>W分裂成x跟y俩树（
{
	if (cur==0) { x=y=0; return; }
	if (ans[cur].w<=W)
	{
		x=cur;
		k_split_weight(rightson,W,rightson,y);//cur的左子树都归到x，右子树继续更新
	}
	else
	{
		y=cur;
		k_split_weight(leftson,W,x,leftson);//cur的右子树归到y，左子树继续更新
	}
	push_up(cur); 
}
void k_split_rank(int cur,int S,int &x,int &y)//按排名分裂。将前S个和后面剩余的分裂成x跟y俩树（ 
{
	if (cur==0) { x=y=0; return; }
	if (ans[leftson].siz+1<=S) 
	{
		x=cur;
		k_split_rank(rightson,S-ans[leftson].siz-1,rightson,y);//S要减去左子树和cur本身的siz 
	}
	else
	{
		y=cur;
		k_split_rank(leftson,S,x,leftson);
	}
	push_up(cur);
}
int k_merge(int x,int y)
{
	if (x==0||y==0) return x+y;
	if (ans[x].pri>ans[y].pri)//比较键值 
	{
		ans[x].r=k_merge(ans[x].r,y);//x右子树和y合并 
		push_up(x);
		return x;
	}
	else
	{
		ans[y].l=k_merge(x,ans[y].l);//x和y左子树合并 
		push_up(y);
		return y;
	}
}
void k_insert(int W)//加入一个元素 
{
	int x,y;
	k_split_weight(Root,W-1,x,y);//按权值分裂出来要插入的位置（ 
	Root=k_merge(k_merge(x,k_create(W)),y);//合并回去 
}
inline void k_delete(int W)//删除一个元素 
{
	int x,y,z;
	k_split_weight(Root,W,x,z); 
	k_split_weight(x,W-1,x,y);//两步分出来只包含元素W的树y 
	if (y) y=k_merge(ans[y].l,ans[y].r);//只删除一个点（ 
	Root=k_merge(k_merge(x,y),z);//合并回去 
}
//合并回去不要忘了更新Root啊QAQ 
inline int k_rank(int W)//查询值对应的排名 
{
	int x,y,ANS;
	k_split_weight(Root,W-1,x,y);//拆出<W的树 
	ANS=ans[x].siz+1;//再返回这个树大小+1（ 
	Root=k_merge(x,y);//合回去，更新Root啊———————你吗 
	return ANS;
}
inline int k_at(int pos)//查询排名对应的值 
{
	int cur=Root;
	while (ans[leftson].siz+1!=pos)//直接利用bst性质找
	{
		if (ans[leftson].siz+1>pos) cur=leftson;
		else { pos=pos-ans[leftson].siz-1; cur=rightson; }
	}
	return ans[cur].w;
}
inline int k_low(int W)//查询前驱 
{
	int cur,x,y,ANS;
	k_split_weight(Root,W-1,x,y);//分出<W的树x 
	cur=x;
	while (rightson) cur=rightson;//跑出x中的最大值即可 
	ANS=ans[cur].w;
	Root=k_merge(x,y);
	return ANS;
}
inline int k_high(int W)//查询后继 
{
	int cur,x,y,ANS;
	k_split_weight(Root,W,x,y);//分出>W的树x（也即分出<=W的树y） 
	cur=y;
	while (leftson) cur=leftson;//跑出y中的最小值即可 
	ANS=ans[cur].w;
	Root=k_merge(x,y);
	return ANS;
}

int main()
{
//	for (int i=1;i<=10;i++) printf("%d\n",k_random());
	k_random();
	int n;
	scanf("%d",&n);
	int opt,x;
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",&opt,&x);
		if (opt==1) k_insert(x);
		else if (opt==2) k_delete(x);
		else if (opt==3) printf("%d\n",k_rank(x));
		else if (opt==4) printf("%d\n",k_at(x));
		else if (opt==5) printf("%d\n",k_low(x));
		else printf("%d\n",k_high(x));
	}
	return 0;
}

fhq_Treap文艺平衡树（区间翻转）

unsigned int SEED=1037;
inline unsigned int k_random() { return SEED=SEED*(unsigned int)19260817%2147483647; }
#define MAXN (int)(1e5+233)
struct Node
{
	int w,l,r,siz,pri; bool tag;
}ans[MAXN];
int tot=0,Root=0;
#define leftson ans[cur].l
#define rightson ans[cur].r
#define push_up(X) ans[X].siz=ans[ans[X].l].siz+ans[ans[X].r].siz+1
#define push_down(X) if (ans[X].tag) { swap(ans[X].l,ans[X].r); ans[ans[X].l].tag^=1; ans[ans[X].r].tag^=1; ans[X].tag=0; }

inline int k_create(int w)//建点 
{
	tot++;
	ans[tot].w=w;
	ans[tot].l=ans[tot].r=0;
	ans[tot].siz=1;
	ans[tot].pri=k_random();
	ans[tot].tag=0;//初始化标记 
	return tot;
}
void k_split_rank(int cur,int S,int &x,int &y)//按排名分裂 
{
	if (cur==0) { x=y=0; return; }
	push_down(cur);//↓↓↓↓ 
	if (ans[leftson].siz+1<=S)
	{
		x=cur;
		k_split_rank(rightson,S-ans[leftson].siz-1,rightson,y);
	}
	else
	{
		y=cur;
		k_split_rank(leftson,S,x,leftson);
	}
	push_up(cur);//↑↑↑↑ 
}
int k_merge(int x,int y) 
{
	if (x==0||y==0) return x+y;
	if (ans[x].pri>ans[y].pri)
	{
		push_down(x);//↓↓↓↓ 
		ans[x].r=k_merge(ans[x].r,y);
		push_up(x);//↑↑↑↑ 
		return x;
	}
	else
	{
		push_down(y);//↓↓↓↓ 
		ans[y].l=k_merge(x,ans[y].l);
		push_up(y);//↑↑↑↑ 
		return y;
	}
}
void k_insert(int w) { Root=k_merge(Root,k_create(w)); }
void k_reverse(int l,int r)
{
	int x,y,z;
	k_split_rank(Root,l-1,x,y);
	k_split_rank(y,r-l+1,y,z);
	ans[y].tag^=1;
	Root=k_merge(k_merge(x,y),z);
}
void dfs(int cur)
{
	if (!cur) return;
	push_down(cur);//↓↓↓↓ 
	dfs(leftson);
	printf("%d ",ans[cur].w);
	dfs(rightson);
	return;
}

int main()
{
	k_random();
	int n,m;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++) k_insert(i);
	for (int i=1,L,R;i<=m;i++)
	{
		scanf("%d%d",&L,&R);
		k_reverse(L,R);
	}
	dfs(Root);
	return 0;
}

可持久化线段树

（主席树）

可持久化的根据是，当每次只修改线段树内一个叶的信息时，线段树需要修改的节点只有一条深度log的链。

可持久化线段树2（静态第k小）

#define MAXN (int)(2e5+233)
#define MID ((l+r)>>1)
#define ls(CUR) t[CUR].ls
#define rs(CUR) t[CUR].rs
#define siz(CUR) t[CUR].siz
#define push_up(CUR) t[CUR].siz=t[ls(CUR)].siz+t[rs(CUR)].siz
int rt[MAXN];
struct Node
{
	int ls,rs;
	int siz;
}t[(int)(1e7+233)];//在有撤销操作时，可以和平衡树一样利用节点回收。 
int cnt=0;

void change(int ct,int lstcur,int &cur,int l,int r,int k)
{
	if (!cur) cur=++cnt;//新建节点 
	if (l==r) { t[cur].siz+=k; return; }//单点修改 
	int mid=MID;
	if (ct<=mid)
	{
		rs(cur)=rs(lstcur);//没修改就接上去（ 
		ls(cur)=++cnt;//修改了就裂一个节点 
		t[ls(cur)]=t[ls(lstcur)];//先赋跟原本一样 
		change(ct,ls(lstcur),ls(cur),l,mid,k); //递归下去更新 
	}
	else
	{
		ls(cur)=ls(lstcur);
		rs(cur)=++cnt;
		t[rs(cur)]=t[rs(lstcur)];
		change(ct,rs(lstcur),rs(cur),mid+1,r,k);
	}
	push_up(cur);//↑↑↑↑ 
}


int query(int qrk,int curl,int curr,int l,int r)//模板：静态区间第k小。利用可持久化线段树可加减的性质，利用[1,r]的线段树减去[1,l-1]的线段树得到[l,r]的线段树，进行查询。 
{
	if (l==r) return l;
	int mid=MID,tmp=siz(ls(curr))-siz(ls(curl));
	if (qrk<=tmp) return query(qrk,ls(curl),ls(curr),l,mid);
	else return query(qrk-tmp,rs(curl),rs(curr),mid+1,r);
}
int n,Q;
int a[MAXN],len;
int lsh[MAXN];

int main()
{
	scanf("%d%d",&n,&Q);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]),lsh[i]=a[i];
	sort(lsh+1,lsh+n+1);
	len=unique(lsh+1,lsh+n+1)-lsh-1;//离散化 
	for (int i=1;i<=n;i++) change(lower_bound(lsh+1,lsh+len+1,a[i])-lsh,rt[i-1],rt[i],1,len,1);//lower_bound(lsh+1,lsh+len+1,a[i])-lsh以得到a[i]的排名 
	for (int i=1,l,r,k;i<=Q;i++)
	{
		scanf("%d%d%d",&l,&r,&k);
		printf("%d\n",lsh[query(k,rt[l-1],rt[r],1,len)]);
	}
	return 0;
}

自然溢出区间哈希

#define MAXN 1007
char s[MAXN];
#define ULL unsigned long long
ULL hs[MAXN];
ULL Base=19260817,P[MAXN];
int n;
inline void INIT()
{
	P[0]=1;
	for (int i=1;i<=n;i++) hs[i]=hs[i-1]*Base+s[i],P[i]=P[i-1]*Base;
}
inline ULL Hash(int l,int r) { return hs[r]-hs[l-1]*P[r-l+1]; }

int main()
{
	scanf("%d",&n);
	scanf("%s",s+1);
	INIT();
	for (int i=1;i<=n;i++)
		for (int j=i;j<=n;j++)
			for (int k=i;k<=j;k++) printf("%c",s[k]); printf(":%llu\n",Hash(i,j));
}

KMP字符串匹配

确定模式串在主串中出现的次数和位置。

$\text{Step 1}$：前缀函数 $nex[i]$ ，表示模式串最长的相等的真前后缀长度。即：

\[nex[i]=max\{j\}，j<i\ 且\ T[1,j]=T[i-j+1,i] \]

$\text{Step 2}$：数组$f[i]$，表示主串的前$i$个字符的后缀与模式串前缀能匹配的最大长度。即：

\[f_i=max\{j\}，j\leq i \ 且 \ T[1,j]=S[i-j+1,i] \]

引理：

若$j0$是$nex[i]$的一个候选项，那么小于$j0$的最大$nex[i]$候选项为$nex[j0]$。

继续算：

如果$j$是$nex[i]的候选项$，那么$j-1$一定是$nex[i-1]$的候选项。

反过来就可以让$j=（nex[i-1]的候选项）+1$作为$j$的预候选项，也就是：

\[nex[i-1]+1,nex[nex[i-1]]+1... \]

比较这些位置和位置$i$上的数就好辽。

求解$nex$

	for (int i=2,j=0;i<=n;i++)
	{
		while (j>0&&s[i]!=s[j+1]) j=nex[j];
		if (a[i]==a[j+1]) j++;
		nex[i]=j;
	}

求解$f$

	for (int i=1,j=0;i<=m;i++)
	{
		while (j>0&&(j==n||b[i]!=a[j+1])) j=nex[j];
		if (b[i]==a[j+1]) j++;
		f[i]=j;
	}

大抵是太久沉迷口胡不写码了。染上了线段树不开四倍的坏习惯。！！！！！！！！！！！

多测要清空！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！

网络最大流

#include <queue>
#include <stack>
#define ll long long
int n,m,s,t;
int maxnode;
#define MAXN (207)//一定要认真算点和边数555
#define MAXM (5007)
queue<int> q;
stack<int> st;
int dep[MAXN];
const ll inf=(ll)(1e16);
struct qwq
{
	int nex,to;
	ll w;
}e[MAXM<<1];
int h[MAXN],tot=1;//tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1tot=1
int h1[MAXN];

inline void add(int x,int y,ll z)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	e[tot].w=z;
	h[x]=tot;
}

inline int bfs()
{
	for (int i=1;i<=maxnode;i++) dep[i]=0;
	dep[s]=1; q.push(s);
	while (!q.empty())
	{
		int x=q.front(); q.pop();
		for (int i=h[x],y;i;i=e[i].nex)
		{
			y=e[i].to;
			if (e[i].w>0&&dep[y]==0)
			{
				dep[y]=dep[x]+1;
				q.push(y);
			}
		}
	}
	for (int i=1;i<=maxnode;i++) h1[i]=h[i];
	return dep[t];
}

ll dfs(int x,ll F)
{
	if (x==t) return F;
	ll tf;
	for (int i=h1[x],y;i;i=e[i].nex)
	{
		h1[x]=i;
		y=e[i].to;
		st.push(e[i].w);
		if (dep[y]==dep[x]+1&&e[i].w>0)
		{
			tf=dfs(y,min(F,e[i].w));
			if (tf==0)
			{
				dep[y]=2*MAXN;
				continue;
			}
			e[i^1].w+=tf;
			e[i].w-=tf;
			return tf;
		}
		st.pop();
	}
	return 0;
}
ll ans=0;
inline void Dinic() { while (bfs()) ans+=dfs(s,inf); }

int main()
{
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for (int i=1,x,y;i<=m;i++)
	{
		ll z;
		scanf("%d%d%lld",&x,&y,&z);
		add(x,y,z); add(y,x,0);
	}
	maxnode=n;
	Dinic();
	printf("%lld\n",ans);
	return 0;
}

最小费用最大流


#include <queue>
#define MAXN (int)(5e3+233)
#define MAXM (int)(5e4+233)
#define ll long long
int n,m,s,t;
int maxnode;
const ll inf=(ll)(1e16);
struct qwq
{
	int nex,to;
	ll w,v;//w为流量，v为费用
}e[MAXM<<1];
int h[MAXN],tot=1;//注意tot的初始化值为1。清空h和tot
inline void add(int x,int y,ll z,ll u)
{
	e[++tot].to=y;
	e[tot].nex=h[x];
	e[tot].w=z;
	e[tot].v=u;
	h[x]=tot;
}
int cnt[MAXN],pre[MAXN];
ll dis[MAXN],mxf[MAXN];
bool vis[MAXN];
queue<int> q;
inline ll spfa()
{
	for (int i=1;i<=maxnode;i++) dis[i]=inf,vis[i]=false,cnt[i]=0,pre[i]=0,mxf[i]=-1;
	while (!q.empty()) q.pop();

	dis[s]=0; vis[s]=true; mxf[s]=inf; q.push(s);
	while (!q.empty())
	{
		int x=q.front(); q.pop(); vis[x]=false;
		for (int i=h[x],y;i;i=e[i].nex)
		{
			if (e[i].w<=0) continue;
			y=e[i].to;
			if (dis[y]>dis[x]+e[i].v)
			{
				dis[y]=dis[x]+e[i].v;
				mxf[y]=min(mxf[x],e[i].w);
				pre[y]=i;
				if (!vis[y])
				{
					cnt[y]++;
					q.push(y); vis[y]=true;
				}
			}
		}
	}
	if (dis[t]==inf) return 0;
	return dis[t];
}
ll maxflow=0;
inline ll flow()
{
	ll p=0,mincost=0;
	while ((p=spfa())>0)
	{
		maxflow+=mxf[t];
		mincost+=dis[t]*mxf[t];
		int x=t;
		while (x!=s)
		{
			e[pre[x]].w-=mxf[t];
			e[pre[x]^1].w+=mxf[t];
			x=e[pre[x]^1].to;
		}
	}
	if (p==-1) return -1;
	return mincost;
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&s,&t);
	ll z,F;
	for (int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d%lld%lld",&x,&y,&z,&F);
		add(x,y,z,F); add(y,x,0,-F);
	}
	maxnode=n;
	ll fff=flow();
	printf("%lld %lld\n",maxflow,fff);
}

矩形面积并

顺带复习一下unique的使用。二分可以lower_bound代替

矩形面积并

#define ll long long
#define MAXN (int)(1e5+233)
struct qwq
{
	ll l,r,y,del;
}e[MAXN<<1];
ll x[MAXN<<1];
int ccc=0,tot=0;
inline void add(ll u1,ll u2,ll y,ll del)
{
	e[++tot]=(qwq){u1,u2,y,del};
}
bool operator < (const qwq &A,const qwq &B)
{
	return A.y<B.y;
}
int sum;
ll ans[MAXN<<4],cnt[MAXN<<4];
#define lson (cur<<1)
#define rson (cur<<1|1)
#define push_up if (cnt[cur]>0) ans[cur]=x[r+1]-x[l]; else if (l==r) ans[cur]=0; else ans[cur]=ans[lson]+ans[rson];
inline int bina(ll X)
{
	int l=1,r=sum;
	while (l<r)
	{
		int mid=(l+r)>>1;
		if (x[mid]>=X) r=mid;
		else l=mid+1;
	}
	return l;
}
void change(int cur,int l,int r,int cl,int cr,ll del)
{
	if (cl<=l&&r<=cr)
	{
		cnt[cur]+=del;
		push_up;
		return;
	}
	int mid=(l+r)>>1;
	if (cl<=mid) change(lson,l,mid,cl,cr,del);
	if (cr>mid) change(rson,mid+1,r,cl,cr,del);
	push_up;
}

int main()
{
	int n;
	scanf("%d",&n);
	ll u1,v1,u2,v2;
	for (int i=1;i<=n;i++)
	{
		scanf("%lld%lld%lld%lld",&u1,&v1,&u2,&v2);
		add(u1,u2,v1,1); add(u1,u2,v2,-1);
		x[++ccc]=u1; x[++ccc]=u2;
	}
	sort(x+1,x+ccc+1); sum=unique(x+1,x+ccc+1)-x-1;
	sort(e+1,e+tot+1);
	ll answer=0;
	for (int i=1;i<tot;i++)
	{
		int L=bina(e[i].l),R=bina(e[i].r)-1;
		change(1,1,sum-1,L,R,e[i].del);
		answer+=ans[1]*(e[i+1].y-e[i].y);
	}
	printf("%lld\n",answer);
	return 0;
}

离线二位数点

放在这有点意味不明

离线二维数点

#define MAXN (int)(2e6+233)//具体使用的时候注意考虑值域进行离散化
int c[MAXN],a[MAXN];
#define lowbit(A) (A&(-A))
int maxn=0;
inline void add(int x,int k)
{
	while (x<=maxn)
	{
		c[x]+=k;
		x+=lowbit(x);
	}
	return;
}
inline int que(int x)
{
	int sum=0;
	while (x>0)
	{
		sum+=c[x];
		x-=lowbit(x);
	}
	return sum;
}
inline int query(int x,int y) { return que(y)-que(x-1); }

struct qwq
{
	int id,loc,del,x;
}e[MAXN<<1];//询问拆
bool operator < (const qwq &A,const qwq &B)
{
	return A.loc<B.loc;
}
int ans[MAXN];

int main()
{
	int n;
	scanf("%d",&n);
	int tot=0;
	int m;
	scanf("%d",&m);
	for (int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		maxn=max(maxn,a[i]);
	}
	for (int i=1,l,r,x;i<=m;i++)
	{
		scanf("%d%d%d",&l,&r,&x);
		e[++tot]=(qwq){i,l-1,-1,x};
		e[++tot]=(qwq){i,r,1,x};
	}
	sort(e+1,e+tot+1);
	int p=0; while (p<tot&&e[p+1].loc==0) p++;
	for (int i=1;i<=n;i++)
	{
		add(a[i],1);
		while (p<tot&&e[p+1].loc==i)
		{
			p++;
			ans[e[p].id]+=e[p].del*query(1,e[p].x);
		}
	}
	for (int i=1;i<=m;i++) printf("%d\n",ans[i]);
	return 0;
}

字典树

trie：对每个文本串t，计算t是多少个模式串si的前缀

#define MAXP (int)(3e6+233)
#define MAXN (int)(1e5+233)
string s[MAXN];
string t;
int n,q;

struct qwq
{
	int sum,typ;
	int son[63];
	qwq() { for (int i=1;i<=62;i++) son[i]=0; sum=typ=0; }
}e[MAXP];
int tot=0;

inline int p(char C) { if ('a'<=C&&C<='z') return (int)(C-'a'+1); else if ('A'<=C&&C<='Z') return (int)(C-'A'+1+26); return (int)(C-'0'+1+26+26); }
void print(int x)
{
	cout<<x<<' '<<e[x].sum<<endl;
	for(int i=1;i<=62;i++)
	{
		if(!e[x].son[i])continue;
		print(e[x].son[i]);
	}
}
void cre(int typ)
{
	e[++tot].typ=typ;
	e[tot].sum=0;
	for (int i=1;i<=62;i++) e[tot].son[i]=0;
}
void add(int cur,int I,int x)
{
	e[cur].sum++;
	if (x>=s[I].size()) return;
	if (!e[cur].son[p(s[I][x])]) { cre(p(s[I][x])); e[cur].son[p(s[I][x])]=tot; }
	add(e[cur].son[p(s[I][x])],I,x+1);
	return;
}
int sear(int cur,int x)
{
	if (x==t.size())
	{
		return e[cur].sum;
	}
	if (!e[cur].son[p(t[x])]) return 0;
	return sear(e[cur].son[p(t[x])],x+1);
}

void R()
{
	tot=0; cre(0);
	scanf("%d%d",&n,&q);
	for (int i=1;i<=n;i++)
	{
		cin>>s[i];
		add(1,i,0);
	}
	while (q--)
	{
		cin>>t;
		printf("%d\n",sear(1,0));
	}
	return;
}

posted @ 2021-09-15 16:10 Kan_kiz 阅读(296) 评论(1) 编辑收藏举报

刷新页面返回顶部

【模板复习+重构（ 重 新 开 始 ）记录+注解】+【错误记录】

快速幂_取余

线段树_区间加

线段树2_区间乘_区间加

gcd

树状数组_单点加_区间查询

树链剖分

单调队列

单调栈

dijkstra

Dijkstra_priority_queue_optimized

缩点

无向图边双联通分量缩点

割点

二分

1.整数区间上二分

(I)查找最小的答案

(II)查找最大的答案

(III)实数域二分

乘法逆元

线性求逆元

阶乘求逆元

二分图判定

SPFA求负环

带权并查集

李超树

01分数规划

set/multiset

线性筛素数

组合数问题模板

fhq_treap

可持久化线段树

自然溢出区间哈希

KMP字符串匹配

引理：

继续算：

网络最大流

最小费用最大流

矩形面积并

离线二位数点

字典树

公告

【模板复习+重构（重新开始）记录+注解】+【错误记录】