范数（Norm）是一种关于向量的函数，是向量“长度”概念及其推广。在线性代数、泛函分析及相关的数学领域，可用范数来度量一个向量的“长度”。在中学里我们学过一个向量的模长(长度)是向量中各元素平方和的平方根，比如向量(3,4)的模长就是5，这里模长其实是向量(3,4)的一种范数——L2范数，向量的范数除了L2范数外，还有其他定义，如L0范数、L1范数和L∞范数，下面将一一介绍上述提及的这几个范数概念。
1 L0范数
若向量X = (x1, x2, …, xn)，则向量X的L0范数为
\[{\left\| {\bf{x}} \right\|_0} = {\bf{x}}中所有非零元素个数
\]
若向量A = (0, 3, 6)，向量A中有1个元素为0，2个非零元素 (3和6)，则A对应L0范数为
\[{\left\| {\bf{A}} \right\|_0} = {\rm{2}}
\]
在机器学习中压缩感知(compressive sensing)领域，很多时候希望最小化目标向量的 L0范数。但L0范数的最优化在数学上被认为是个NP-hard问题，即求解很复杂，所以许多压缩感知模型是将最小化目标向量的 L0范数转化为最小化目标向量的 L1范数。
2 L1范数
若向量X = (x1, x2, …, xn)，则向量X的L1范数为
\[\begin{array}{l}
{\left\| {\bf{x}} \right\|_1} = \left| {{x_1}} \right| + \left| {{x_2}} \right| + \cdots \left| {{x_n}} \right| \\
\quad \;\;{\rm{ = }}\sum\limits_{i = 1}^n {\left| {{x_i}} \right|} \\
\end{array}\]
若向量A = (0, 3, 6)，则A对应L1范数为
\[{\left\| {\bf{A}} \right\|_1} = \left| {\rm{0}} \right|{\rm{ + }}\left| {\rm{3}} \right|{\rm{ + }}\left| {\rm{6}} \right|{\rm{ = 3 + 6 = 9}}
\]
最小化目标向量的 L1范数求解比最小化目标向量的 L0范数容易些，可通过最优化算法得到对应的可行解。但L1范数有一个问题，就是L1范数的导数不易求，所以许多机器学习问题中遇到 L1范数最小化问题会转为L2范数最小化问题。
3 L2范数
若向量X = (x1, x2, …, xn)，则向量X的L2范数为
\[ \begin{array}{l}
{\left\| {\bf{x}} \right\|_2} = \sqrt {{{\left| {{x_1}} \right|}^{\rm{2}}}{\rm{ + }}{{\left| {{x_{\rm{2}}}} \right|}^{\rm{2}}}{\rm{ + }} \cdots {\rm{ + }}{{\left| {{x_n}} \right|}^{\rm{2}}}} \\
\quad \;\;{\rm{ = }}\sqrt {\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^2}} } \\
\end{array} \]
若向量A = (2, 3, 6)，则A对应L2范数为
\[{\left\| {\bf{A}} \right\|_2} = \sqrt {{2^2} + {3^2} + {6^2}} = \sqrt {4 + 9 + 36} = \sqrt {49} = 7
\]
4 L∞范数
若向量X = (x1, x2, …, xn)，则向量X的L∞范数为
\[{\left\| {\bf{x}} \right\|_\infty } = \max \left( {\left| {{x_1}} \right|\left| {{x_{\rm{2}}}} \right| \cdots \left| {{x_n}} \right|} \right)
\]
若向量A = (2, 3, 6)，则A对应L∞范数为
\[{\left\| {\bf{A}} \right\|_\infty } = \max \left( {2,3,6} \right) = 6
\]
5 Lp范数
Lp范数实际上将L1范数、L2范数和L∞范数统一到一个框架体系中。
若向量X = (x1, x2, …, xn)，则向量X的Lp范数为
\[ \begin{array}{l}
{\left\| {\bf{x}} \right\|_p} = \sqrt[p]{{{{\left| {{x_1}} \right|}^p}{\rm{ + }}{{\left| {{x_{\rm{2}}}} \right|}^p}{\rm{ + }} \cdots {\rm{ + }}{{\left| {{x_n}} \right|}^p}}} \\
\quad \;\;{\rm{ = }}\sqrt[p]{{\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^p}} }} \\
\end{array} \]
关于Lp范数的几何解释可以用单位圆来说明。单位圆是无穷个向量终点组成的集合，这些向量必须满足Lp范数为1且起点为原点。
对于L1范数，它在R2空间中的单位圆是正方形。
对于L2范数，它在R2空间中的单位圆是圆形。
对于L∞范数，它是R2空间中的单位圆也是一个正方形。
对于任何p范数，它是一个超椭圆（具有全等轴）。下面图为p取不同数值，Lp范数对应的单位圆。
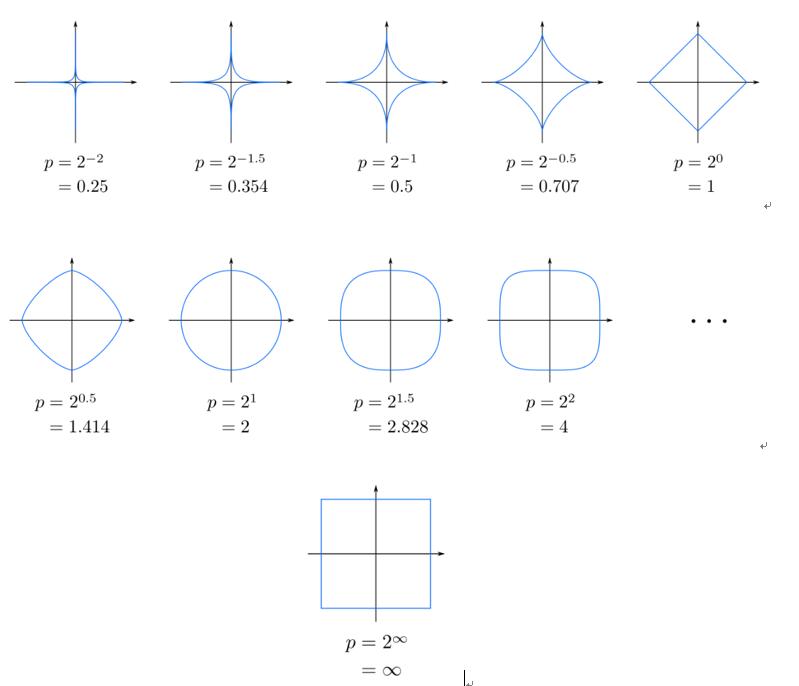
图1 不同p对应的单位圆
