[树的直径]F. Three Paths on a Tree
F. Three Paths on a Tree
Description
You are given an unweighted tree with nn vertices. Recall that a tree is a connected undirected graph without cycles.
Your task is to choose three distinct vertices a,b,ca,b,c on this tree such that the number of edges which belong to at least one of the simple paths between aa and bb, bb and cc, or aa and ccis the maximum possible. See the notes section for a better understanding.
The simple path is the path that visits each vertex at most once.
Input
The first line contains one integer number nn (3≤n≤2⋅1053≤n≤2⋅105) — the number of vertices in the tree.
Next n−1n−1 lines describe the edges of the tree in form ai,biai,bi (1≤ai1≤ai, bi≤nbi≤n, ai≠biai≠bi). It is guaranteed that given graph is a tree.
output
In the first line print one integer resres — the maximum number of edges which belong to at least one of the simple paths between aa and bb, bb and cc, or aa and cc.
In the second line print three integers a,b,ca,b,c such that 1≤a,b,c≤n1≤a,b,c≤n and a≠,b≠c,a≠ca≠,b≠c,a≠c.
If there are several answers, you can print any.
Examples
Input
8
1 2
2 3
3 4
4 5
4 6
3 7
3 8
Output
5
1 8 6
Note
The picture corresponding to the first example (and another one correct answer):
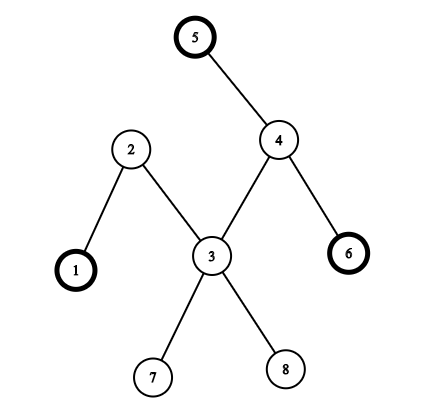
If you choose vertices 1,5,61,5,6 then the path between 11 and 55 consists of edges (1,2),(2,3),(3,4),(4,5)(1,2),(2,3),(3,4),(4,5), the path between 11 and 66 consists of edges (1,2),(2,3),(3,4),(4,6)(1,2),(2,3),(3,4),(4,6) and the path between 55 and 66 consists of edges (4,5),(4,6)(4,5),(4,6). The union of these paths is (1,2),(2,3),(3,4),(4,5),(4,6)(1,2),(2,3),(3,4),(4,5),(4,6) so the answer is 55. It can be shown that there is no better answer.
正确解法:
在树上选出三个点,使他们的边的并集最大。
这引入了树的直径,树的直径的边最长。假设a、b是树的两个直径端点,c是除了a、b的任意一个点
ans=(dis(a,c)+dis(a,b)+dis(b,c))/2;
两次BFS求树的直径与端点:
那么问题来了,怎么求树的直径的呢?这里提供一种两次BFS求树的直径的方法:
先任选一个起点BFS找到最长路的终点,再从终点进行BFS,则第二次BFS找到的最长路即为树的直径;
原理: 设起点为u,第一次BFS找到的终点v一定是树的直径的一个端点
证明: 1) 如果u 是直径上的点,则v显然是直径的终点(因为如果v不是的话,则必定存在另一个点w使得u到w的距离更长,则于BFS找到了v矛盾)
2) 如果u不是直径上的点,则u到v必然于树的直径相交(反证),那么交点到v 必然就是直径的后半段了
所以v一定是直径的一个端点,所以从v进行BFS得到的一定是直径长度

1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #include <algorithm> 5 #include <set> 6 #include <queue> 7 #include <stack> 8 #include <string> 9 #include <cstring> 10 #include <vector> 11 #include <map> 12 //#include <unordered_map> 13 #define mem( a ,x ) memset( a , x ,sizeof(a) ) 14 #define rep( i ,x ,y ) for( int i = x ; i<=y ;i++ ) 15 #define lson l ,mid ,pos<<1 16 #define rson mid+1 ,r ,pos<<1|1 17 using namespace std; 18 typedef long long ll ; 19 typedef pair<int ,int> pii; 20 typedef pair<ll ,int> pli; 21 const int inf = 0x3f3f3f3f; 22 const ll mod=998244353; 23 const int N=1e5+50; 24 int n,xx,yy,pos; 25 int Link[2*N],len=0,bok[2*N],dis[2*N]; 26 int dis1[2*N],dis2[2*N]; 27 int que[2*N]; 28 struct node 29 { 30 int y,next; 31 }e[4*N]; 32 void insert(int xx,int yy) 33 { 34 e[++len].next=Link[xx]; 35 Link[xx]=len; 36 e[len].y=yy; 37 } 38 void dfs(int x) 39 { 40 for(int i=1;i<=n;i++) 41 bok[i]=0,dis[i]=inf; 42 bok[x]=1,dis[x]=0; 43 int head=1,tail=2; 44 que[1]=x; 45 pos=x; 46 while(head<tail) 47 { 48 int u=que[head]; 49 for(int i=Link[u];i;i=e[i].next) 50 { 51 int v=e[i].y; 52 if(bok[v]) continue; 53 bok[v]=1; 54 if(dis[v]>dis[u]+1) 55 { 56 dis[v]=dis[u]+1; 57 que[tail++]=v; 58 } 59 if(dis[v]!=inf&&dis[v]>dis[pos]) 60 pos=v; 61 } 62 head++; 63 } 64 } 65 int main() 66 { 67 scanf("%d",&n); 68 for(int i=1;i<n;i++) 69 { 70 scanf("%d%d",&xx,&yy); 71 insert(xx,yy); 72 insert(yy,xx); 73 } 74 int a,b,c=0; 75 dfs(1),a=pos; 76 dfs(pos),b=pos; 77 for(int i=1;i<=n;i++) dis1[i]=dis[i]; 78 //cout<<a<<endl; 79 dfs(pos); 80 for(int i=1;i<=n;i++) dis2[i]=dis[i]; 81 //cout<<b<<endl; 82 int ans=0; 83 for(int i=1;i<=n;i++) 84 { 85 if(i==a||i==b) continue; 86 if(ans<dis1[i]+dis2[i]) 87 { 88 ans=dis1[i]+dis2[i]; 89 c=i; 90 } 91 } 92 //cout<<c<<endl; 93 printf("%d\n",(ans+dis1[b])/2); 94 printf("%d %d %d\n",a,b,c); 95 96 return 0; 97 }
------------------------------------------------------------------------------------------------------
树形DP
对于每个节点我们要记录两个值:
f1 [ i ] 表示以 i 为根的子树中,i 到叶子结点距离的最大值
f2 [ i ] 表示以 i 为根的子树中,i 到叶子结点距离的次大值
对于一个节点,它到叶子结点距离的最大值和次大致所经过的路径肯定是不一样的
若j是i的儿子,那么(下面的 w [ i ][ j ] 表示 i 到 j 的路径长度):
若 f1 [ i ] < f1 [ j ] + w [ i ][ j ],f2 [ i ] = f1 [ i ],f1 [ i ] = f1 [ j ] + w [ i ][ j ];
否则,若 f2 [ i ] < f1 [ j ] + w [ i ][ j ],f2 [ i ] = f1 [ j ] + w [ i ][ j ];
理解:这样做就是,先看能否更新最大值,若能,它的次大值就是原先的最大值,再更新它的最大值;若不能,就看能不能更新次大值,若能,就更新,不能就不管它
这样的话,最后的答案 answer = max { f1 [ i ] + f2 [ i ] }

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=100005; 6 int n,m,t,ans; 7 int f1[N],f2[N]; 8 int first[N],v[N],w[N],next[N]; 9 void add(int x,int y,int z) 10 { 11 t++; 12 next[t]=first[x]; 13 first[x]=t; 14 v[t]=y; 15 w[t]=z; 16 } 17 void dp(int x,int father) 18 { 19 int i,j; 20 for(i=first[x];i;i=next[i]) 21 { 22 j=v[i]; 23 if(j==father) 24 continue; 25 dp(j,x); 26 if(f1[x]<f1[j]+w[i]) 27 { 28 f2[x]=f1[x]; 29 f1[x]=f1[j]+w[i]; 30 } 31 else if(f2[x]<f1[j]+w[i]) 32 f2[x]=f1[j]+w[i]; 33 ans=max(ans,f1[x]+f2[x]); 34 } 35 } 36 int main() 37 { 38 int x,y,z,i; 39 scanf("%d%d",&n,&m); 40 for(i=1;i<=m;++i) 41 { 42 scanf("%d%d%d",&x,&y,&z); 43 add(x,y,z); 44 add(y,x,z); 45 } 46 dp(1,0); 47 printf("%d",ans); 48 return 0; 49 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号