[图论]强联通分量

暂时不知道这玩意怎么用，暂时不知道啥时候用这玩意....

在有向图G中，如果两点互相可达，则称这两个点强连通，如果G中任意两点互相可达，则称G是强连通图。

定理： 1、一个有向图是强连通的，当且仅当G中有一个回路，它至少包含每个节点一次。

            2、非强连通有向图的极大强连通子图，称为强连通分量（SCC即Strongly Connected Componenet）。

 

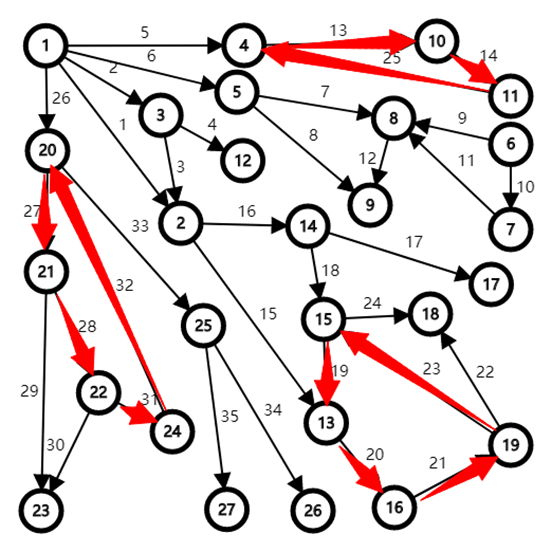
怎么求这个强联通分量呢？

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。总的来说， Tarjan算法基于一个观察，即：同处于一个SCC中的结点必然构成DFS树的一棵子树。 我们要找SCC，就得找到它在DFS树上的根。

-----------------------------------------------------------------------------------

tin[u]代表访问u节点的时间戳，low[u]代表u为根节点的dfs树中时间戳最小的顶点的时间戳。

访问到u时，tin[u]=low[u]=++id;

u入栈。

由u的顶点找下点v。若v未访问过，dfs(v);　　low[u]=min(low[u],low[v]);

若v已经访问过，则说明形成了环， low[u]=min(low[u],tin[v]);

若tin[u]==low[u] 则开始出栈，一直出到u。其中 用belong数组来记录这个点属于的块。

 

 1 void tarjan(int u)
 2 {
 3     tin[u]=low[u]=++id;
 4     s.push(u);
 5     bok[u]=1;
 6     for(int i=Link[u];i;i=e[i].next)
 7     {
 8         int v=e[i].y;
 9         if(!tin[v])
10         {
11             tarjan(v);
12             low[u]=min(low[u],low[v]);
13         }
14         else if(bok[v])
15         {
16             low[u]=min(low[u],tin[v]);
17         }
18     }
19     if(tin[u]==low[u])
20     {
21         Bcnt++;
22         while(true)
23         {
24             int v=s.top();
25             s.pop();
26             bok[v]=0;
27             belong[v]=Bcnt;
28             if(u==v)    break;
29         }
30     }
31 }
View Code

 

 

1 for(int i=1;i<=n;i++)
2             if(!tin[i])
3                 tarjan(i);
4         int f=1;
5         for(int i=1;i<=n;i++)
6             if(belong[i]!=1)
7                 f=0;
8         if(f)   printf("Yes\n");
9         else    printf("No\n");
View Code

 

边双联通分量：在求有向图的强联通分量时，只要不走父边，就是边联通分量。

 1 void tarjan(int u,int fa)
 2 {
 3     tin[u]=low[u]=++id;
 4     s.push(u);
 5     bok[u]=1;
 6     for(int i=Link[u];i;i=e[i].next)
 7     {
 8         int v=e[i].y;
 9         if(v==fa)   continue;
10         if(!tin[v])
11         {
12             tarjan(v,u);
13             low[u]=min(low[u],low[v]);
14         }
15         else if(bok[v])
16         {
17             low[u]=min(low[u],tin[v]);
18         }
19     }
20     if(tin[u]==low[u])
21     {
22         Bcnt++;
23         while(true)
24         {
25             int v=s.top();
26             s.pop();
27             bok[v]=0;
28             belong[v]=Bcnt;
29             if(u==v)    break;
30         }
31     }
32 }
View Code

 点双联通分量

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <algorithm>
  4 #include <vector> 
  5 #include <stack>
  6 
  7 using namespace std;
  8 
  9 const int maxn = 105, maxm = maxn * 2;
 10 
 11 int n, m, tot, dfs_clock, bcc_cnt;
 12 
 13 int h[maxn], dfn[maxn], low[maxn], iscut[maxn], bccno[maxn];
 14 
 15 vector<int> bcc[maxn];
 16  
 17 struct edge1
 18 {
 19     int v, next;
 20 }a[maxm];
 21 
 22 struct EDGE
 23 {
 24     int u, v;
 25 };
 26 
 27 stack<EDGE> s;
 28 
 29 void add(int x, int y)
 30 {
 31     a[tot].v = y;
 32     a[tot].next = h[x];
 33     h[x] = tot++;
 34 }
 35 
 36 int dfs(int u, int fa)
 37 {
 38     int lowu = dfn[u] = ++dfs_clock;
 39     int child = 0;
 40     for (int i = h[u]; ~i; i = a[i].next)
 41     {
 42         int v = a[i].v;
 43         EDGE e = (EDGE){u, v};//所谓栈中存储的是边
 44         if (!dfn[v])
 45         {
 46             s.push(e);//把沿途遍历到的边都加入栈
 47             child++;
 48             int lowv = dfs(v, u);
 49             lowu = min(lowu, lowv);
 50             if (lowv >= dfn[u])
 51             {
 52                 iscut[u] = 1;//我们发现了一个割顶，也就说明当前栈中已经保存了一个点双的集合。
 53                 bcc_cnt++;//bcc_cnt从1开始。
 54                 bcc[bcc_cnt].clear();//应付多组数据，应该先清空。
 55                 for(;;)
 56                 {
 57                     EDGE x = s.top(); s.pop();
 58                     if (bccno[x.u] != bcc_cnt)
 59                     {
 60                         bcc[bcc_cnt].push_back(x.u);
 61                         bccno[x.u] = bcc_cnt;
 62                     }
 63                     if (bccno[x.v] != bcc_cnt)
 64                     {
 65                         bcc[bcc_cnt].push_back(x.v);
 66                         bccno[x.v] = bcc_cnt;
 67                     }//这两段的意思是，把边集中涉及到的点全部取出来，把他们的bccno[]设置成当前的bcc_cnt
 68                     if (x.u == u && x.v == v) break;//一直弹栈直到弹到了当前加入的边，break。
 69                 }
 70             }
 71         }else if (dfn[v] < dfn[u] && v != fa)
 72         {
 73             s.push(e);//把沿途遍历到的边都加入栈。
 74             lowu = min(lowu, dfn[v]);
 75         }
 76     }
 77     if (fa == 0 && child == 1)
 78     {
 79         iscut[u] = 0;
 80     }
 81     low[u] = lowu;
 82     return lowu;
 83 }
 84 
 85 int main()
 86 {
 87     freopen("无向图的点双联通分量.in","r",stdin);
 88     scanf("%d%d", &n, &m);
 89     memset(h, -1, sizeof h); tot = dfs_clock = bcc_cnt = 0;
 90     for (int i = 1; i <= m; i++)
 91     {
 92         int x, y;
 93         scanf("%d%d", &x, &y);
 94         add(x, y); add(y, x);
 95     }
 96     dfs(1, 0);
 97     for (int i = 1; i <= bcc_cnt; i++)
 98     {
 99         for (int j = 0; j < bcc[i].size(); j++)
100             printf("%d ", bcc[i][j]);
101         printf("\n");
102     }
103     return 0;
104 }#include <cstdio>
105 #include <cstring>
106 #include <algorithm>
107 #include <vector> 
108 #include <stack>
109 
110 using namespace std;
111 
112 const int maxn = 105, maxm = maxn * 2;
113 
114 int n, m, tot, dfs_clock, bcc_cnt;
115 
116 int h[maxn], dfn[maxn], low[maxn], iscut[maxn], bccno[maxn];
117 
118 vector<int> bcc[maxn];
119  
120 struct edge1
121 {
122     int v, next;
123 }a[maxm];
124 
125 struct EDGE
126 {
127     int u, v;
128 };
129 
130 stack<EDGE> s;
131 
132 void add(int x, int y)
133 {
134     a[tot].v = y;
135     a[tot].next = h[x];
136     h[x] = tot++;
137 }
138 
139 int dfs(int u, int fa)
140 {
141     int lowu = dfn[u] = ++dfs_clock;
142     int child = 0;
143     for (int i = h[u]; ~i; i = a[i].next)
144     {
145         int v = a[i].v;
146         EDGE e = (EDGE){u, v};//所谓栈中存储的是边
147         if (!dfn[v])
148         {
149             s.push(e);//把沿途遍历到的边都加入栈
150             child++;
151             int lowv = dfs(v, u);
152             lowu = min(lowu, lowv);
153             if (lowv >= dfn[u])
154             {
155                 iscut[u] = 1;//我们发现了一个割顶，也就说明当前栈中已经保存了一个点双的集合。
156                 bcc_cnt++;//bcc_cnt从1开始。
157                 bcc[bcc_cnt].clear();//应付多组数据，应该先清空。
158                 for(;;)
159                 {
160                     EDGE x = s.top(); s.pop();
161                     if (bccno[x.u] != bcc_cnt)
162                     {
163                         bcc[bcc_cnt].push_back(x.u);
164                         bccno[x.u] = bcc_cnt;
165                     }
166                     if (bccno[x.v] != bcc_cnt)
167                     {
168                         bcc[bcc_cnt].push_back(x.v);
169                         bccno[x.v] = bcc_cnt;
170                     }//这两段的意思是，把边集中涉及到的点全部取出来，把他们的bccno[]设置成当前的bcc_cnt
171                     if (x.u == u && x.v == v) break;//一直弹栈直到弹到了当前加入的边，break。
172                 }
173             }
174         }else if (dfn[v] < dfn[u] && v != fa)
175         {
176             s.push(e);//把沿途遍历到的边都加入栈。
177             lowu = min(lowu, dfn[v]);
178         }
179     }
180     if (fa == 0 && child == 1)
181     {
182         iscut[u] = 0;
183     }
184     low[u] = lowu;
185     return lowu;
186 }
187 
188 int main()
189 {
190     freopen("无向图的点双联通分量.in","r",stdin);
191     scanf("%d%d", &n, &m);
192     memset(h, -1, sizeof h); tot = dfs_clock = bcc_cnt = 0;
193     for (int i = 1; i <= m; i++)
194     {
195         int x, y;
196         scanf("%d%d", &x, &y);
197         add(x, y); add(y, x);
198     }
199     dfs(1, 0);
200     for (int i = 1; i <= bcc_cnt; i++)
201     {
202         for (int j = 0; j < bcc[i].size(); j++)
203             printf("%d ", bcc[i][j]);
204         printf("\n");
205     }
206     return 0;
207 }
View Code

 

posted @ 2019-07-06 19:53  kaike  阅读(338)  评论(0)  编辑  收藏  举报