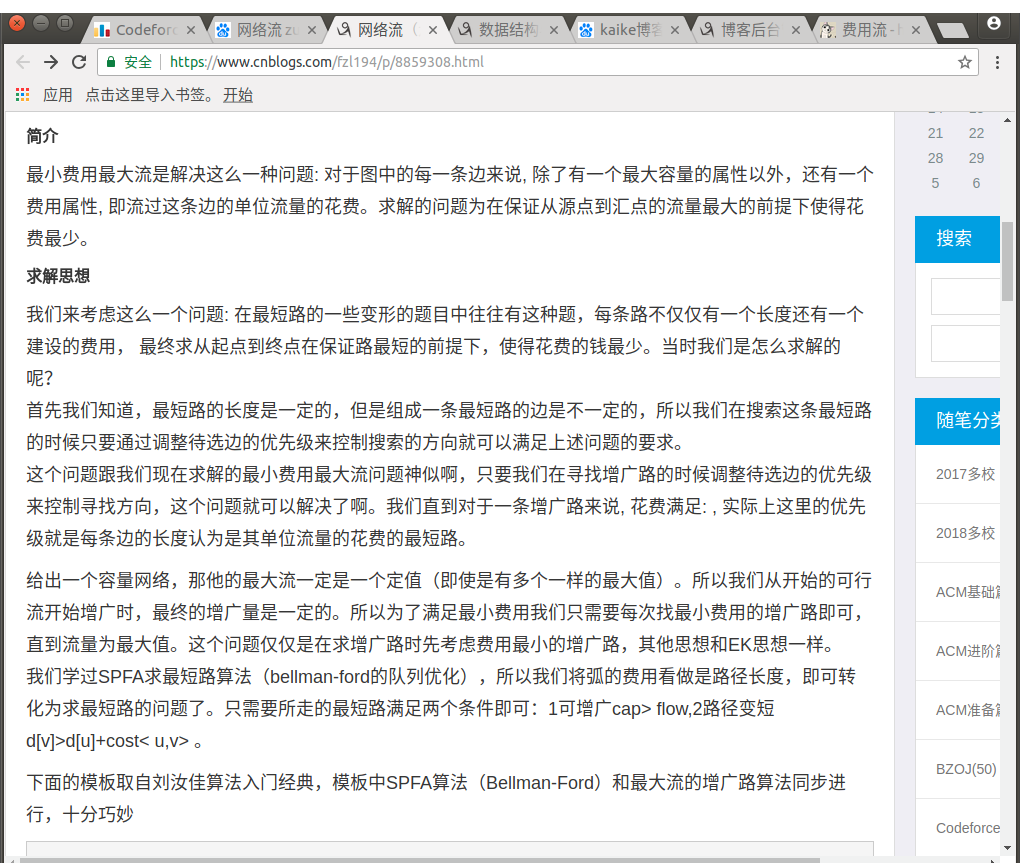
[建模]网络流最大流量最小费用

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<map> 6 #include<set> 7 #include<vector> 8 #include<queue> 9 #include<algorithm> 10 #include<cmath> 11 #include<list> 12 using namespace std; 13 typedef long long ll; 14 const int INF=0x7fffffff; 15 const int N=100000+100; 16 const int M=9999999; 17 const ll mod=1000000000+7; 18 const int maxn = 1000 + 10; 19 struct edge 20 { 21 int u, v, c, f, cost; 22 edge(int u, int v, int c, int f, int cost):u(u), v(v), c(c), f(f), cost(cost){} 23 }; 24 vector<edge>e; 25 vector<int>G[maxn]; 26 int a[maxn];//找增广路每个点的水流量 27 int p[maxn];//每次找增广路反向记录路径 28 int d[maxn];//SPFA算法的最短路 29 int inq[maxn];//SPFA算法是否在队列中 30 int n=5, m=7; 31 void init(int n) 32 { 33 for(int i = 0; i <= n; i++)G[i].clear(); 34 e.clear(); 35 } 36 void addedge(int u, int v, int c, int cost) 37 { 38 e.push_back(edge(u, v, c, 0, cost)); 39 e.push_back(edge(v, u, 0, 0, -cost)); 40 int m = e.size(); 41 G[u].push_back(m - 2); 42 G[v].push_back(m - 1); 43 } 44 bool bellman(int s, int t, int& flow, long long & cost) 45 { 46 for(int i = 0; i <= n + 1; i++)d[i] = INF;//Bellman算法的初始化 47 memset(inq, 0, sizeof(inq)); 48 d[s] = 0;inq[s] = 1;//源点s的距离设为0,标记入队 49 p[s] = 0;a[s] = INF;//源点流量为INF(和之前的最大流算法是一样的) 50 51 queue<int>q;//Bellman算法和增广路算法同步进行,沿着最短路拓展增广路,得出的解一定是最小费用最大流 52 q.push(s); 53 while(!q.empty()) 54 { 55 int u = q.front(); 56 q.pop(); 57 inq[u] = 0;//入队列标记删除 58 for(int i = 0; i < G[u].size(); i++) 59 { 60 edge & now = e[G[u][i]]; 61 int v = now.v; 62 if(now.c > now.f && d[v] > d[u] + now.cost) 63 //now.c > now.f表示这条路还未流满(和最大流一样) 64 //d[v] > d[u] + e.cost Bellman 算法中边的松弛 65 { 66 d[v] = d[u] + now.cost;//Bellman 算法边的松弛 67 p[v] = G[u][i];//反向记录边的编号 68 a[v] = min(a[u], now.c - now.f);//到达v点的水量取决于边剩余的容量和u点的水量 69 if(!inq[v]){q.push(v);inq[v] = 1;}//Bellman 算法入队 70 } 71 } 72 } 73 if(d[t] == INF)return false;//找不到增广路 74 flow += a[t];//最大流的值,此函数引用flow这个值,最后可以直接求出flow 75 cost += (long long)d[t] * (long long)a[t];//距离乘上到达汇点的流量就是费用 76 for(int u = t; u != s; u = e[p[u]].u)//逆向存边 77 { 78 e[p[u]].f += a[t];//正向边加上流量 79 e[p[u] ^ 1].f -= a[t];//反向边减去流量 (和增广路算法一样) 80 } 81 return true; 82 } 83 int MincostMaxflow(int s, int t, long long & cost) 84 { 85 cost = 0; 86 int flow = 0; 87 while(bellman(s, t, flow, cost));//由于Bellman函数用的是引用,所以只要一直调用就可以求出flow和cost 88 return flow;//返回最大流,cost引用可以直接返回最小费用 89 } 90 int main() 91 { 92 init(n); 93 addedge(1,2,20,12); 94 addedge(1,3,16,3); 95 addedge(3,2,10,6); 96 addedge(2,4,4,18); 97 addedge(3,4,20,9); 98 addedge(2,5,14,3); 99 addedge(4,5,8,6); 100 ll ans; 101 cout<<MincostMaxflow(1,5,ans)<<endl;//zui da liu liang 102 cout<<ans<<endl;//zui xiao fei yong 103 104 return 0; 105 }
最大流量:22
最小费用:330
最小生成树:
刚开始想最小生成树裸题嘛,后来发现只能沿着x轴或y轴,但是他们之间的距离是不会变的呀,从斜边长变成了两直角边之和。
然后就是把每两个点之间的距离都求出来。因为七个点之间任意两个点都可以到达。
最后就是生成树裸题了。从A出发,每次找一个最近的点,加入队列中,其他点更新距离。重复这样的过程,n-1次。(n-1条边)
答案为:A-G-F-D-E D-C-B

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<map> 6 #include<set> 7 #include<vector> 8 #include<queue> 9 #include<algorithm> 10 #include<cmath> 11 #include<list> 12 using namespace std; 13 typedef long long ll; 14 const int INF=0x7fffffff; 15 const int N=100000+100; 16 const int M=9999999; 17 const ll mod=1000000000+7; 18 int n=7; 19 int a[10][10],dis[10],bok[10]; 20 int summ=0; 21 struct node 22 { 23 int x,y; 24 }b[10]; 25 void init() 26 { 27 for(int i=1;i<=7;i++) 28 scanf("%d %d",&b[i].x,&b[i].y); 29 for(int i=1;i<=7;i++) 30 for(int j=i+1;j<=7;j++) 31 { 32 int kk=abs(b[j].x-b[i].x)+abs(b[j].y-b[i].y); 33 a[i][j]=kk; 34 a[j][i]=kk; 35 } 36 for(int i=1;i<=7;i++) 37 { 38 for(int j=1;j<=7;j++) 39 printf("%d ",a[i][j]); 40 printf("\n"); 41 } 42 } 43 void prim(int S) 44 { 45 memset(dis,10,sizeof(dis)); 46 memset(bok,0,sizeof(bok)); 47 bok[S]=1; 48 for(int i=1;i<=n;i++) 49 dis[i]=a[S][i]; 50 summ=0; 51 for(int i=1;i<n;i++) 52 { 53 int minn=INF,c=0; 54 for(int j=1;j<=n;j++) 55 if(minn>dis[j]&&bok[j]==0) 56 { 57 minn=dis[j]; 58 c=j; 59 } 60 bok[c]=1; 61 summ+=minn; 62 for(int j=1;j<=n;j++) 63 if(dis[j]>a[c][j]&&bok[j]==0) 64 dis[j]=a[c][j]; 65 cout<<c<<" "<<summ<<endl; 66 } 67 } 68 int main() 69 { 70 init(); 71 prim(1); 72 cout<<summ<<endl; 73 74 return 0; 75 }
No matter how you feel, get up , dress up , show up ,and never give up.



