[CF]Codeforces Round #515 (Div. 3)

A. Vova and Train

Description

Vova plans to go to the conference by train. Initially, the train is at the point 11 and the destination point of the path is the point LL. The speed of the train is 11 length unit per minute (i.e. at the first minute the train is at the point 11, at the second minute — at the point 22 and so on).

There are lanterns on the path. They are placed at the points with coordinates divisible by vv (i.e. the first lantern is at the point vv, the second is at the point 2v2v and so on).

There is also exactly one standing train which occupies all the points from ll to rr inclusive.

Vova can see the lantern at the point pp if pp is divisible by vv and there is no standing train at this position (p∉[l;r]p∉[l;r]). Thus, if the point with the lantern is one of the points covered by the standing train, Vova can't see this lantern.

Your problem is to say the number of lanterns Vova will see during the path. Vova plans to go to tt different conferences, so you should answer tt independent queries.

Input

The first line of the input contains one integer tt (1≤t≤1041≤t≤104) — the number of queries.

Then tt lines follow. The ii-th line contains four integers Li,vi,li,riLi,vi,li,ri (1≤L,v≤1091≤L,v≤109, 1≤l≤r≤L1≤l≤r≤L) — destination point of the ii-th path, the period of the lantern appearance and the segment occupied by the standing train.

Output

Print tt lines. The ii-th line should contain one integer — the answer for the ii-th query.

Examples

Input

4
10 2 3 7
100 51 51 51
1234 1 100 199
1000000000 1 1 1000000000

Output

3
0
1134
0

Note

For the first example query, the answer is 33. There are lanterns at positions 22, 44, 66, 88 and 1010, but Vova didn't see the lanterns at positions 44 and 66 because of the standing train.

For the second example query, the answer is 00 because the only lantern is at the point 5151 and there is also a standing train at this point.

For the third example query, the answer is 11341134 because there are 12341234 lanterns, but Vova didn't see the lanterns from the position 100100 to the position 199199 inclusive.

For the fourth example query, the answer is 00 because the standing train covers the whole path.

 

正确解法：

一条路上有L米 [1,L] ，其中v的整数倍有灯笼，在[l,r]中没有灯笼，问这条路上总共有多少个灯笼。

简单的一个一个求整数倍肯定tle。

那就算 l是不是v的整数倍，r是不是v的整数倍。

这样分为四种情况后，发现只要验证 l 是不是整数倍就ok了。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<string>
 4 #include<cstring>
 5 #include<map>
 6 #include<set>
 7 #include<vector>
 8 #include<queue>
 9 #include<algorithm>
10 #include<cmath>
11 using namespace std;
12 typedef long long ll;
13 const int inf=0x7fffffff;
14 const int N=1010;
15 const int M=100000+10;
16 ll T,l,v,ll1,rr;
17 int main()
18 {
19     scanf("%d",&T);
20     while(T--)
21     {
22         ll ans=0;
23         scanf("%d %d %d %d",&l,&v,&ll1,&rr);
24         ans=l/v;
25         if(ll1%v==0)
26             ans=ans-(rr/v-ll1/v)-1;
27         else
28             ans=ans-(rr/v-ll1/v);
29         printf("%d\n",ans);
30     }
31 
32     return 0;
33 }
View Code

 

 

B. Heaters

Description

Vova's house is an array consisting of nn elements (yeah, this is the first problem, I think, where someone livesin the array). There are heaters in some positions of the array. The ii-th element of the array is 11 if there is a heater in the position ii, otherwise the ii-th element of the array is 00.

Each heater has a value rr (rr is the same for all heaters). This value means that the heater at the position posposcan warm up all the elements in range [pos−r+1;pos+r−1][pos−r+1;pos+r−1].

Vova likes to walk through his house while he thinks, and he hates cold positions of his house. Vova wants to switch some of his heaters on in such a way that each element of his house will be warmed up by at least one heater.

Vova's target is to warm up the whole house (all the elements of the array), i.e. if n=6n=6, r=2r=2 and heaters are at positions 22 and 55, then Vova can warm up the whole house if he switches all the heaters in the house on (then the first 33 elements will be warmed up by the first heater and the last 33 elements will be warmed up by the second heater).

Initially, all the heaters are off.

But from the other hand, Vova didn't like to pay much for the electricity. So he wants to switch the minimumnumber of heaters on in such a way that each element of his house is warmed up by at least one heater.

Your task is to find this number of heaters or say that it is impossible to warm up the whole house.

Input

The first line of the input contains two integers nn and rr (1≤n,r≤10001≤n,r≤1000) — the number of elements in the array and the value of heaters.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤10≤ai≤1) — the Vova's house description.

Output

Print one integer — the minimum number of heaters needed to warm up the whole house or -1 if it is impossible to do it.

Examples

Input

6 2
0 1 1 0 0 1

Output

3

Input

5 3
1 0 0 0 1

Output

2

Note

In the first example the heater at the position 22 warms up elements [1;3][1;3], the heater at the position 33 warms up elements [2,4][2,4] and the heater at the position 66 warms up elements [5;6][5;6] so the answer is 33.

In the second example the heater at the position 11 warms up elements [1;3][1;3] and the heater at the position 55warms up elements [3;5][3;5] so the answer is 22.

 

正确解法：

找第一个放蜡烛的点，然后依次往后面找，下一个蜡烛的位置是 【前一个蜡烛的位置+1，前一个蜡烛的位置+2*r-1】

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<string>
 4 #include<cstring>
 5 #include<map>
 6 #include<set>
 7 #include<vector>
 8 #include<queue>
 9 #include<algorithm>
10 #include<cmath>
11 using namespace std;
12 typedef long long ll;
13 const int inf=0x7fffffff;
14 const int N=1010;
15 const int M=100000+10;
16 int n,r,now=0,ans=0;
17 int a[N];
18 int main()
19 {
20     scanf("%d %d",&n,&r);
21     for(int i=1;i<=n;i++)
22         scanf("%d",&a[i]);
23     int flag=0;
24     for(int i=r;i>=1;i--)
25         if(a[i]==1)
26         {
27             now=i;
28             ans++;
29             flag=1;
30             break;
31         }
32     if(flag==0)
33         {
34             printf("-1\n");
35             return 0;
36         }
37 
38     while(now+r<=n)
39     {
40         flag=0;
41         for(int i=min(now+2*r-1,n);i>=now+1;i--)
42         {
43             if(a[i]==1)
44             {
45                 now=i;
46                 //cout<<now<<endl;
47                 ans++;
48                 flag=1;
49                 break;
50             }
51         }
52         if(flag==0)
53         {
54             printf("-1\n");
55             return 0;
56         }
57     }
58     printf("%d\n",ans);
59 
60     return 0;
61 }
View Code

 

 

C. Books Queries

Description

You have got a shelf and want to put some books on it.

You are given qq queries of three types:

  1. L idid — put a book having index idid on the shelf to the left from the leftmost existing book;
  2. R idid — put a book having index idid on the shelf to the right from the rightmost existing book;
  3. ? idid — calculate the minimum number of books you need to pop from the left or from the right in such a way that the book with index idid will be leftmost or rightmost.

You can assume that the first book you will put can have any position (it does not matter) and queries of type 33are always valid (it is guaranteed that the book in each such query is already placed). You can also assume that you don't put the same book on the shelf twice, so idids don't repeat in queries of first two types.

Your problem is to answer all the queries of type 33 in order they appear in the input.

Note that after answering the query of type 33 all the books remain on the shelf and the relative order of books does not change.

Input

The first line of the input contains one integer qq (1≤q≤2⋅1051≤q≤2⋅105) — the number of queries.

Then qq lines follow. The ii-th line contains the ii-th query in format as in the problem statement. It is guaranteed that queries are always valid (for query type 33, it is guaranteed that the book in each such query is already placed, and for other types, it is guaranteed that the book was not placed before).

It is guaranteed that there is at least one query of type 33 in the input.

In each query the constraint 1≤id≤2⋅1051≤id≤2⋅105 is met.

Output

Print answers to queries of the type 33 in order they appear in the input.

Examples

Input

8
L 1
R 2
R 3
? 2
L 4
? 1
L 5
? 1

Output

1
1
2

 

正确解法：

依次放序号为i的书，放在左边或右边，问 序号为i的书 min（从左边拿，从右边拿）。

桶排序，一个 l=r=0 记录这个书的下标。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<string>
 4 #include<cstring>
 5 #include<map>
 6 #include<set>
 7 #include<vector>
 8 #include<queue>
 9 #include<algorithm>
10 #include<cmath>
11 using namespace std;
12 typedef long long ll;
13 const int inf=0x7fffffff;
14 const int N=2*1e5+10;
15 const int M=100000+10;
16 int a[N],l=0,r=1,q,x;
17 char s;
18 int main()
19 {
20     scanf("%d",&q);
21     while(q--)
22     {
23         cin>>s;
24         scanf("%d",&x);
25         if(s=='L')
26             a[x]=l--;
27         else if(s=='R')
28             a[x]=r++;
29         else
30             printf("%d\n",min(a[x]-l,r-a[x])-1);
31     }
32 
33     return 0;
34 }
View Code

 

D. Boxes Packing

Description

Maksim has 𝑛n objects and 𝑚m boxes, each box has size exactly 𝑘k. Objects are numbered from 11 to 𝑛n in order from left to right, the size of the 𝑖i-th object is 𝑎𝑖ai.

Maksim wants to pack his objects into the boxes and he will pack objects by the following algorithm: he takes one of the empty boxes he has, goes from left to right through the objects, and if the 𝑖i-th object fits in the current box (the remaining size of the box is greater than or equal to 𝑎𝑖ai), he puts it in the box, and the remaining size of the box decreases by 𝑎𝑖ai. Otherwise he takes the new empty box and continues the process above. If he has no empty boxes and there is at least one object not in some box then Maksim cannot pack the chosen set of objects.

Maksim wants to know the maximum number of objects he can pack by the algorithm above. To reach this target, he will throw out the leftmost object from the set until the remaining set of objects can be packed in boxes he has. Your task is to say the maximum number of objects Maksim can pack in boxes he has.

Each time when Maksim tries to pack the objects into the boxes, he will make empty all the boxes he has before do it (and the relative order of the remaining set of objects will not change).

Input

The first line of the input contains three integers 𝑛n, 𝑚m, 𝑘k (1≤𝑛,𝑚≤2⋅1051≤n,m≤2⋅105, 1≤𝑘≤1091≤k≤109) — the number of objects, the number of boxes and the size of each box.

The second line of the input contains 𝑛n integers 𝑎1,𝑎2,…,𝑎𝑛a1,a2,…,an (1≤𝑎𝑖≤𝑘1≤ai≤k), where 𝑎𝑖ai is the size of the 𝑖i-th object.

Output

Print the maximum number of objects Maksim can pack using the algorithm described in the problem statement.

Examples

Input

5 2 6
5 2 1 4 2

Output

4

Note

In the first example Maksim can pack only 44 objects. Firstly, he tries to pack all the 55 objects. Distribution of objects will be [5],[2,1][5],[2,1]. Maxim cannot pack the next object in the second box and he has no more empty boxes at all. Next he will throw out the first object and the objects distribution will be [2,1],[4,2][2,1],[4,2]. So the answer is 44.

 

正确解法：

有n个物品，m个书包，每个书包能装k重量。

每个物体为 ai 重量。

只能从前往后装。求最多能装多少个物体？

我们要从后往前走。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<string>
 4 #include<cstring>
 5 #include<map>
 6 #include<set>
 7 #include<vector>
 8 #include<queue>
 9 #include<algorithm>
10 #include<cmath>
11 using namespace std;
12 typedef long long ll;
13 const int inf=0x7fffffff;
14 const int N=2*1e5+100;
15 const int M=100000+10;
16 const ll mod=998244353;
17 int n,m,k;
18 int a[N];
19 int main()
20 {
21     scanf("%d %d %d",&n,&m,&k);
22     for(int i=n;i>=1;i--)
23         scanf("%d",&a[i]);
24     int res=k;
25     for(int i=1;i<=n;i++)
26     {
27         if(res>=a[i])
28         {
29             res-=a[i];
30         }
31         else{
32             m--;
33             if(m==0)
34             {
35                 printf("%d\n",i-1);
36                 return 0;
37             }
38             res=k-a[i];
39         }
40     }
41     printf("%d\n",n);
42     return 0;
43 }
View Code

 

E. Binary Numbers AND Sum

Description

You are given two huge binary integer numbers 𝑎a and 𝑏b of lengths 𝑛n and 𝑚m respectively. You will repeat the following process: if 𝑏>0b>0, then add to the answer the value 𝑎 & 𝑏a & b and divide 𝑏b by 22 rounding down (i.e. remove the last digit of 𝑏b), and repeat the process again, otherwise stop the process.

The value 𝑎 & 𝑏a & b means bitwise AND of 𝑎a and 𝑏b. Your task is to calculate the answer modulo 998244353998244353.

Note that you should add the value 𝑎 & 𝑏a & b to the answer in decimal notation, not in binary. So your task is to calculate the answer in decimal notation. For example, if 𝑎=10102 (1010)a=10102 (1010) and 𝑏=10002 (810)b=10002 (810), then the value 𝑎 & 𝑏a & b will be equal to 88, not to 10001000.

Input

The first line of the input contains two integers 𝑛n and 𝑚m (1≤𝑛,𝑚≤2⋅1051≤n,m≤2⋅105) — the length of 𝑎a and the length of 𝑏b correspondingly.

The second line of the input contains one huge integer 𝑎a. It is guaranteed that this number consists of exactly 𝑛n zeroes and ones and the first digit is always 11.

The third line of the input contains one huge integer 𝑏b. It is guaranteed that this number consists of exactly 𝑚m zeroes and ones and the first digit is always 11.

Output

Print the answer to this problem in decimal notation modulo 998244353.

Examples

Input

4 4
1010
1101

Output

12

Note

he algorithm for the first example:

  1. add to the answer 10102 & 11012=10002=81010102 & 11012=10002=810 and set 𝑏:=110b:=110;
  2. add to the answer 10102 & 1102=102=21010102 & 1102=102=210 and set 𝑏:=11b:=11;
  3. add to the answer 10102 & 112=102=21010102 & 112=102=210 and set 𝑏:=1b:=1;
  4. add to the answer 10102 & 12=02=01010102 & 12=02=010 and set 𝑏:=0b:=0.

So the answer is 8+2+2+0=128+2+2+0=12.

 

正确解法：

有一个a和b字符串，长度都为n。

然后求 a&b ，b/=2; 直到b=0 时停止。求a&b加起来。

我们发现这最终求得是a中的1 对b 前位置的影响。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<string>
 4 #include<cstring>
 5 #include<map>
 6 #include<set>
 7 #include<vector>
 8 #include<queue>
 9 #include<algorithm>
10 #include<cmath>
11 using namespace std;
12 typedef long long ll;
13 const int inf=0x7fffffff;
14 const int N=200000+10;
15 const int M=100000+10;
16 const ll mod=998244353;
17 char s[N];
18 int a[N],b[N],sum[N];
19 ll ans=0;
20 int n,m;
21 int main()
22 {
23     scanf("%d %d",&n,&m);
24     scanf("%s",s+1);
25     for(int i=1;i<=n;i++)
26         a[i]=(int)(s[i]-'0');
27     scanf("%s",s+1);
28     for(int i=1;i<=m;i++)
29         b[i]=(int)(s[i]-'0');
30     sum[0]=0;
31     for(int i=1;i<=m;i++)
32         sum[i]=sum[i-1]+b[i];
33     int aaa=1;
34     for(int i=n;i>=1;i--)
35     {
36         if(a[i]==1)
37         {    ans+=(ll)sum[max(0,m-n+i)]*aaa;
38             ans%=mod;
39          }
40          aaa=(aaa*2)%mod;
41     }
42     cout<<ans<<endl;
43 
44     return 0;
45 }
View Code

 

 

F. Yet another 2D Walking 

Description

Maksim walks on a Cartesian plane. Initially, he stands at the point (0,0)(0,0) and in one move he can go to any of four adjacent points (left, right, up, down). For example, if Maksim is currently at the point (0,0)(0,0), he can go to any of the following points in one move:

  • (1,0)(1,0);
  • (0,1)(0,1);
  • (−1,0)(−1,0);
  • (0,−1)(0,−1).

There are also 𝑛n distinct key points at this plane. The 𝑖i-th point is 𝑝𝑖=(𝑥𝑖,𝑦𝑖)pi=(xi,yi). It is guaranteed that 0≤𝑥𝑖0≤xi and 0≤𝑦𝑖0≤yi and there is no key point (0,0)(0,0).

Let the first level points be such points that 𝑚𝑎𝑥(𝑥𝑖,𝑦𝑖)=1max(xi,yi)=1, the second level points be such points that 𝑚𝑎𝑥(𝑥𝑖,𝑦𝑖)=2max(xi,yi)=2 and so on. Maksim wants to visit all the key points. But he shouldn't visit points of level 𝑖+1i+1 if he does not visit all the points of level 𝑖i. He starts visiting the points from the minimum level of point from the given set.

The distance between two points (𝑥1,𝑦1)(x1,y1) and (𝑥2,𝑦2)(x2,y2) is |𝑥1−𝑥2|+|𝑦1−𝑦2||x1−x2|+|y1−y2| where |𝑣||v| is the absolute value of 𝑣v.

Maksim wants to visit all the key points in such a way that the total distance he walks will be minimum possible. Your task is to find this distance.

Input

The first line of the input contains one integer 𝑛n (1≤𝑛≤2⋅1051≤n≤2⋅105) — the number of key points.

Each of the next 𝑛n lines contains two integers 𝑥𝑖xi, 𝑦𝑖yi (0≤𝑥𝑖,𝑦𝑖≤1090≤xi,yi≤109) — 𝑥x-coordinate of the key point 𝑝𝑖pi and 𝑦y-coordinate of the key point 𝑝𝑖pi. It is guaranteed that all the points are distinct and the point (0,0)(0,0) is not in this set.

Output

Print one integer — the minimum possible total distance Maksim has to travel if he needs to visit all key points in a way described above.

Examples

Input

8
2 2
1 4
2 3
3 1
3 4
1 1
4 3
1 2

Output

15

Note

The picture corresponding to the first example:

There is one of the possible answers of length 1515.

 

正确解法：

在坐标轴上有n个关键点。给出n个坐标点的坐标。

按照 max(x,y) 来分level。只有访问完 level(i) 的所有关键点之后才可以访问 level(i+1)的点。

求访问所有关键点的距离。

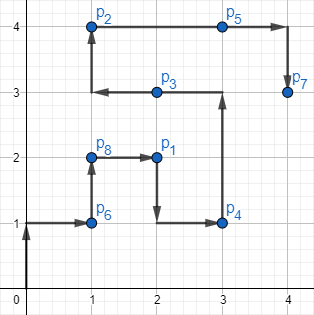
我们把所有关键点排序。按照level，同一level的点 从下到上 从右到左 排序

同一level的点很好找到距离。

那么level之间的距离呢？

设dp[i][0]为访问到 第i个level第一个点的距离。

dp[i][1]为访问到 第i个level最后一个点的距离。

最后加上 min（dp[len][1],dp[len][0]）;

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #include <algorithm>
 6 #include <set>
 7 #include <map>
 8 #include <vector>
 9 using namespace std;
10 typedef long long ll;
11 const int inf=0x7fffffff;
12 const int N=200000+100;
13 struct node
14 {
15     int x,y;
16 }a[N],tmp;
17 vector<node>e[N];
18 int n,xx,yy;
19 ll ans=0;
20 ll dp[N][3];
21 bool cmp(node a,node b)
22 {
23     if(max(a.x,a.y)==max(b.x,b.y))
24     {
25         if(a.x==b.x)    return a.y<b.y;
26         return a.x>b.x;
27     }
28     return max(a.x,a.y)<max(b.x,b.y);
29 }
30 void init()
31 {
32     scanf("%d",&n);
33     for(int i=1;i<=n;i++)
34         scanf("%d %d",&a[i].x,&a[i].y);
35     sort(a+1,a+n+1,cmp);
36 }
37 ll solve(ll tmp)
38 {
39     if(tmp<0)   return -tmp;
40     return tmp;
41 }
42 int main()
43 {
44     init();
45     tmp.x=0;    tmp.y=0;
46     e[0].push_back(tmp);
47     e[0].push_back(tmp);
48     int t=1,len=1;
49     while(t<=n)
50     {
51         e[len].push_back(a[t]);
52         int cc=t;
53         while(t<n&&max(a[t+1].x,a[t+1].y)==max(a[cc].x,a[cc].y))
54             t++;
55         e[len++].push_back(a[t]);
56         ans+=solve((ll)a[t].y-a[cc].y)+solve((ll)a[t].x-a[cc].x);
57         t++;
58     }
59     len--;
60     //dp[1][0]=dp[1][1]=0;
61     for(int i=1;i<=len;i++)
62     {
63         ll dis00=solve(e[i-1][0].x-e[i][0].x)+solve(e[i-1][0].y-e[i][0].y);
64         ll dis01=solve(e[i-1][0].x-e[i][1].x)+solve(e[i-1][0].y-e[i][1].y);
65         ll dis10=solve(e[i-1][1].x-e[i][0].x)+solve(e[i-1][1].y-e[i][0].y);
66         ll dis11=solve(e[i-1][1].x-e[i][1].x)+solve(e[i-1][1].y-e[i][1].y);
67         dp[i][0]=min(dp[i-1][0]+dis10,dp[i-1][1]+dis00);
68         dp[i][1]=min(dp[i-1][1]+dis01,dp[i-1][0]+dis11);
69     }
70     ans+=min(dp[len][0],dp[len][1]);
71     cout<<ans<<endl;
72 
73     return 0;
74 }
View Code

 

posted @ 2019-03-20 12:13  kaike  阅读(426)  评论(0)  编辑  收藏  举报