[图论]二叉树的编号

 

小球下落

Description

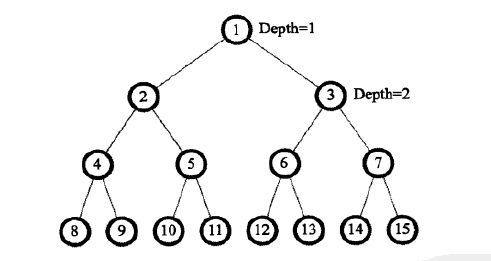
 有一棵二叉树，最大深度为D，且所有的叶子深度都相同。所有结点从上到下从左到右编号为1，2，3，…，2eD-1。在结点1处放一个小球，它会往下落。每个结点上都有一个开关，初始全部关闭，当每次有小球落到一个开关上时，它的状态都会改变。当小球到达一个内结点时，如果该结点的开关关闭，则往上走，否则往下走，直到走到叶子结点，如下图所示。
    一些小球从结点1处依次开始下落，最后一个小球将会落到哪里呢？输入叶子深度D和小球个数I，输出第I个小球最后所在的叶子编号。假设I不超过整棵树的叶子数；D<=20。输出最多包含1000组数据。

Examples

Input

4 2
3 4
10 1
2 2
8 128
16 12345

Output

12
7
512
3
255
36358

 

正确解法：

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N = 30;
int d,t;
int a[100010];
int main()
{
    while(scanf("%d %d",&d,&t)!=EOF)
    {
        int ans=1;
        d--;
        d=1<<d;
        memset(a,0,sizeof(a));
        //cout<<d<<endl;
        while(t--)
        {
            ans=1;
            while(ans<d)
            {
                a[ans]=!a[ans];
                ans= a[ans]? ans*2:ans*2+1;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

 当我们用一个数组并且一个个模拟小球的时候，浪费时间和空间。

我们可不可以直接模拟最后一个小球呢？

当第一个小球的时候，肯定跑到左边第一个 　　8

第二个小球　　　　　　　跑到右边的左边第一个　　12

第三个小球　　　　　　　跑到左边的右边的左边　　10

第四个　　　　　　　　　　　　　　　　　　　　　14

　　　　　　　　　　　　　　　　　　　　　　　　9

　　　　　　　　　　　　　　　　　　　　　　　　13

　　　　　　　　　　　　　　　　　　　　　　　　11

　　　　　　　　　　　　　　　　　　　　　　　　15

可以一层一层的遍历，个数是奇数的话，下面就是 （个数+1）/2 因为有一半去了右边

个数是偶数的话，（个数）/2

int ans=1;
        for(int i=1;i<d;i++)
        {
            if(t%2) {
                ans*=2;
                t=(t+1)/2;
            }
            else
            {
                ans=ans*2+1;
                t=t/2;
            }