Counting Rectangles(二维数组前缀和)
题目描述:
You have \(n\) rectangles, the \(i\)-th rectangle has height \(h_i\) and width \(w_i\).
You are asked \(q\) queries of the form \(h_s w_s h_b w_b\).
For each query output, the total area of rectangles you own that can fit a rectangle of height \(h_s\) and width \(w_s\) while also fitting in a rectangle of height \(h_b\) and width \(w_b\). In other words, print \(\sum{h_i⋅w_i}\) for \(i\) such that \(hs<hi<hb\) and \(ws<wi<wb.\)
Please note, that if two rectangles have the same height or the same width, then they cannot fit inside each other. Also note that you cannot rotate rectangles.
Please note that the answer for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).
输入描述:
The first line of the input contains an integer \(t (1≤t≤100)\) — the number of test cases.
The first line of each test case two integers \(n,q (1≤n≤10^5; 1≤q≤10^5)\) — the number of rectangles you own and the number of queries.
Then \(n\) lines follow, each containing two integers \(h_i,w_i (1≤h_i,w_i≤1000)\) — the height and width of the \(i\)-th rectangle.
Then \(q\) lines follow, each containing four integers $h_s,w_s,h_b,w_b (1≤h_s<h_b, w_s<w_b≤1000) $— the description of each query.
The sum of \(q\) over all test cases does not exceed \(10^5\), and the sum of \(n\) over all test cases does not exceed \(10^5\).
输出描述:
For each test case, output \(q\) lines, the \(i\)-th line containing the answer to the \(i\)-th query.
提醒:
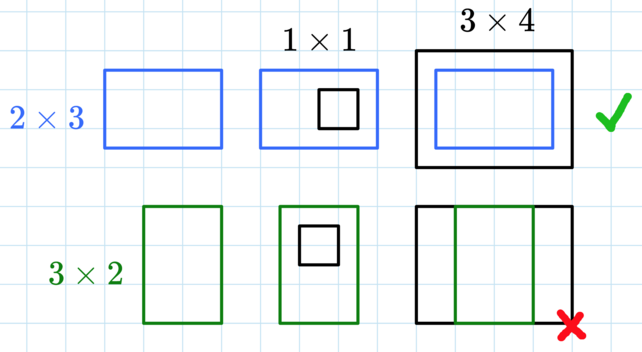
In the first test case, there is only one query. We need to find the sum of areas of all rectangles that can fit a \(1×1\) rectangle inside of it and fit into a \(3×4\) rectangle.
Only the \(2×3\) rectangle works, because \(1<2\) (comparing heights) and \(1<3\) (comparing widths), so the \(1×1\) rectangle fits inside, and \(2<3\) (comparing heights) and \(3<4\) (comparing widths), so it fits inside the \(3×4\) rectangle. The \(3×2\) rectangle is too tall to fit in a \(3×4\) rectangle. The total area is \(2⋅3=6\).
题解:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010;
int T = 1;
int n, q;
LL a[N][N]; // 利用二维数组来存储, a[i][j] 代表长 i ,宽为 j 的矩阵的面积
void solve()
{
scanf("%d%d", &n, &q);
memset(a, 0, sizeof a); // 每次都将矩阵初始化为0
for (int i = 1; i <= n; i++)
{
int x, y;
scanf("%d%d", &x, &y);
a[x][y] += x * y; // 将矩阵的值变为面积(注意要加)
}
for (int i = 1; i <= 1001; i++)
{
for (int j = 1; j <= 1001; j++)
{
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + a[i][j]; // 将矩阵做前缀和
}
}
while (q--)
{
int h1, w1, h2, w2, l, r;
scanf("%d%d%d%d", &h1, &w1, &h2, &w2);
// 题目要求长和宽相等的矩阵也不符合要求,所以一定要严格要求长和宽都小于或大于所给的两个矩阵
h1 = h1 + 1;
w1 = w1 + 1;
h2 = h2 - 1;
w2 = w2 - 1;
printf("%lld\n", a[h2][w2] - a[h1 - 1][w2] - a[h2][w1 - 1] + a[h1 - 1][w1 - 1]); // 求前缀和
}
}
int main()
{
// ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
scanf("%d", &T);
while (T--)
{
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号