《谁能证明：标准波面的光若能汇集于一点，则它们的光程长度必然相等》 回复

《谁能证明：标准波面的光若能汇集于一点，则它们的光程长度必然相等》  https://tieba.baidu.com/p/7692891691    。

 

6 楼

这是要把多个 光脉冲 合为同相位的一束光 ？        XDDongfang     陈彼方º

 

 

7 楼

这个问题 似乎 是   单个激光器 的 功率 的 瓶颈，   单个 “谐振腔” （谐振体）  无法产生更大功率 的 激光  。

 

让 多束 激光 谐振，   合为 一束 激光，   可以 突破 单个激光器 的 功率极限，   产生 更大 功率 的 激光  。

 

但 应该 思考 ：     如果 解锁了 这个技能，   会 带来 什么样 的 影响 ？

 

从   XDDongfang  透露 的 资料 来看，   共量子论 应该 比较 全面 的 揭示 了 光本性，   同时，  共量子论  应用了 大量 数学计算 和 复杂模型，  包括 三维空间 里 的 模型，  比如 三维空间 里 的 光子模型 ？（笑）    这些 理论内容 应该会 详细 的 描绘 出 光子 特性  。

 

拓变论  全科学理论体系 认为   “光子应该是光量子，量子是量子，粒子是粒子”  ，   这也是 研究 光本性 的 一个 好的 思路  。

 

我以前写过一篇  《我对 量子力学 提出了一个 修正，名为 “K氏修正”》   https://tieba.baidu.com/p/6631549518    。

 

 

 

 

 

 

 

刚 想了一下 用 色散 来 进行 “时间移项” 的 过程， 其实 单色光 虽然 不能用 色散 来 达到 距离差， 但 和 色散类似， 对于 单色光，只要 让 1000 个 光脉冲 每一次 的 光的方向 稍微偏转一点（类似 色散）就行了呀， 接下来的技术和过程， 就和 利用色散来时间移相一样了

你会说，那要怎么让 每次 脉冲 的 光 偏转 ？ 机械 没有这个 反应速度 和 精度 。我说， 既然 我们现在都玩 飞米技术 飞秒技术 了，那显然，参与这个游戏 的 角色 也只能 是 这个 层面 的， 那就让 光子 来 控制 光子 吧 ！

让 一个 光子 碰撞 另一个 光子， 使 另一个 光子 改变 方向 。怎么碰撞 ？ 干涉 就是 碰撞 。 两束光 融合在一起会 产生 干涉条纹， 干涉条纹 就 意味 着 两束光 的 光子 让 对方 的 光子 改变 前进 方向 了 。

 

 

 

 

 

 

11 楼

回复 7 楼  dons222

 

你说  “所谓的移动法我是考虑过的，无论是平动还是转动在我所考虑过的模型中都无法实现--即交点上始终满足波前相位相同。” 

 

用 色散 把 一束光 里 不同 颜色 的 光 分开摊平 获得 距离差， 对 这些 不同 颜色 的 光 移相，  让 它们 的 相位中心 重合  。 这些 不同颜色 的 光 最后 又要 合在一起，此时，它们 的 相位中心 重合  。 

 

这些 不同颜色 的 光 是 通过 光栅 控制 其 行进方向  来 合为 一束光  。   但 到底 是 合为 一束光，  还是 集中 到 某个 交点（焦点） ？

 

不管 是 合为 一束光 还是  集中 到 某个 交点（焦点），     一束 激光 分成 不同颜色 的 光  可以用 光栅 控制 光 的 方向 再 把 它们 合起来 ，   那 为什么 就 不能 把  1000 束 激光（脉冲） 也用 光栅 控制 方向 ，  把  1000 束 激光（脉冲） 也 合起来 呢  ？

 

先 用 光子 碰撞 光子，  让  1000 个 激光脉冲 的 行进方向 发生 偏转，   改变其 路径，  产生 距离差，   用  距离差 来 移相，  使得  1000 个 脉冲 的 相位中心 同步，  然后 把  1000 个 脉冲 合起来，  合为 一束光  。

 

"用 光子 碰撞 光子，  让  1000 个 激光脉冲 的 行进方向 发生 偏转" ，   这是 第一个 步骤，   是 我 提出来 的，   而 第二个 步骤  “把  1000 个 脉冲 合起来，  合为 一束光”，   这个 完全可以 和    色散移相 一样， 用 光栅 控制 偏转后的 1000 个 脉冲 的 行进方向 ，   把  1000 个 脉冲 合起来  。

 

 

dons222  一直 在讲  波阵面 、球面波、柱面波、平面波、椭球面波，无穷小点的发光源 、衍射极限  ……   

 

看起来  dons222  还 抱着 惠更斯原理 这一类 模型，     惠更斯原理 是 很 老式 的 ，   大可不必 使用  。    使用 惠更斯原理 这一类  模型 会 让 事物 变得 复杂，   甚至 南辕北辙  。

 

所以 dons222 在 本帖 提出的 这个 定理，    思维机器 还 和 他  辩 得  津津有味，    实际上，   既然 都要 把  惠更斯原理 抛弃 了 ，   那 这个 定理 的 什么  “标准波面” 、“光程长度” 、“汇集于一点”  、“费马原理” 、“等效的真空光程 或 飞行时间”  、“必然相等”  ……   全是 不知所云  。

 

这个 定理 就是 个 不知所云  。

 

 

我 以前写过 《用 双边干涉 来 计算 小孔衍射》   https://tieba.baidu.com/p/6245538427   。    当然，    这篇 文章 距离 认识 光 的 衍射 干涉 还有 一段 距离  。

 

 

用  惠更斯原理 或者 波动理论 无法解释 色散移相，    移相 让 不同 颜色（频率） 的 光  的 相位中心重合，  就是  让 它们 的 波峰 的 峰点 重合，  这样 叠加起来 可以得到 最大功率，  问题是，  对于  不同频率 的  “波”  来说，   它们 的 第一个 波峰 的 峰点 重合 了，   能 保证 后面 的 波峰 的 峰点 也 重合 吗  ？     当然 不能 保证  。   除非  这些 波 的 频率 是 倍频 关系，  即 频率 是 某个 基频 的 整数倍，   就像 傅里叶级数  。 

 

但 就算 是 傅里叶级数，   也只有 基波 的 波峰 的 峰点 能 和  所有 谐波（倍频） 的 峰点 重合，  除了 基波，   只有 频率 能 整除 的 两个 谐波 能 做到 一个 谐波 的 每一个 波峰 峰点 都 和 另一个 谐波 的 波峰 峰点 重合  。   频率 不能 整除 的 两个 谐波 不能 做到 一个 谐波 的 每一个 波峰 峰点 都 和 另一个 谐波 的 波峰 峰点 重合  。

 

 

关于 光子 的 碰撞（干涉），   我 现在 可以 给出 一个 定理 ：

 

真空中，   只有 2 个 光子 a 、b，    光子 a 沿 直线 AB 前进，  光子 b 沿 直线 BC 前进，    AB 、BC 相交于 C，  AB 、BC 确定 一个平面 P 。 光子 a 和 光子 b 在 C 点 相遇，  发生 干涉，  干涉 后，  a 、b 的 运动方向 都 发生 改变，   沿着 新 方向 继续 前进，   a 、b  仍然 在  平面 P 上  。   通过 控制  a 、b  （相遇）干涉 时 的 运动方向，  可以 准确 的 得到 干涉 后 a 、b 的 运动方向  。

 

这个 定理 称为   单光子干涉定理，   又名  光子碰撞定理  。

 

我 就 先 剧透 到 这，    更多 剧情，   就 看 共量子论 来 解密  。   XDDongfang

 

未来，   在  《K 量子论》 里，   我会 讲到 光 的 衍射 干涉 的 原理 和 理论模型，   当然，  只是 大体 的 原理 和 理论模型，  精细计算 和 深层性质 还是 看 共量子论  。

 

 

本来 我对  量子行为 、光 的 衍射 干涉 、电子波 、德布罗意波 ，   这些 我 想 的 也还 不太清楚，   也 不 急着 研究，   但 这次 dons222 在 这个 帖 里 提出了 问题，  而且 自从 认识 dons222  以来 的 这段时间，    他 经常 讲起   光学测量 、激光测量 、激光探伤 、X 光测量 、X 光探伤  ……

 

昨天 dons222 又 在  《漫画 《怪谈档案》 看到的 一道 数学题 和 一段 科学趣闻》   https://tieba.baidu.com/p/7685425731   2 楼 回复 说 

“

可以了解下，现在认知物质结构的主要手段之一，主要是xrd(x射线衍射成像)、xrf(x射线荧光谱)、紫外-可见-红外光谱分析、太赫兹波谱分析、还有那种一定速度下的带电粒子在磁场里的回旋半径的仪器(好像就叫质谱仪)，还有一种电子衍射花样的分析方法比较有意思

”

 

这些 实在太有趣了，    把  我 的 灵感 激发 了 ，    把  量子行为 、光 的 衍射 干涉 、电子波 、德布罗意波  这些 串起来 了  。

 

虽说如此，    但 道路 还是 曲折 的，    夜晚，  我 望向 窗外 的 路灯，  路灯 很亮，   周围 的 光晕 里 看到 一格一格 的，   大概 是 路灯 本身 就是像 复眼一样 一格一格 的 构造 的 缘故 吧  。

 

但  路灯 一格一格 的 造成 光晕 也是 一格一格  的  ？

 

还有，   我在 《黎耀天 共量子 我拍了 几张照片 给你们 当 素材》    https://tieba.baidu.com/p/6378662957   里 发的 照片， 比如 下面这张，   强烈 的 阳光 在 照片 上 留下了 一道  长长 的 光弧    。

 

想着 路灯 光晕 的 一格一格  和 照片 里 的 光弧，    我 又 迷惘 了  。

 

注 ：    不要 长时间 直视 路灯 或 其它 灯，    现在 的 灯光技术 很先进，   比如 LED ，  耗电小，亮度大，  直视 比较亮 的 灯 时间过长， 会 损伤视力  。

 

 

 

 

 

 

 

 

 

12 楼

回复  11 楼   dons222

 

一个问题 是，    一模一样  的  1000 个 激光器 在 同时 发出 1000 束 激光，  是否 这些激光 的 相位 是 相同 的 ？

 

两束光 合到一起 会 干涉 散开，    这 也许 是 大自然 有意为之  。   如果 多束光 可以 任意 的 叠加在一起 合成 一束光，  那 就可以 无限 的 叠加下去 由 无数束 光 叠加在一起 合成 一束 能量 无限 大 的 光  。     这 会否 造成 一些 “失控” 的 后果 ？

 

对于 物质来说，  密度 也是 有限 的，   也不能把 无限多 的 物质 揉到一个 有限 的 体积 里  。    当然，  要说  黑洞，   那 另说  。

 

贝塞尔光束   先不看了，  留个悬念  。 

 

后来想到，  实际上，  大多数 的 情况，  光 是 直线传播 的，    比如，   成像 就是 基于  “光 沿 直线 传播”  。  日常中，   一个光子 并不会 随时随地 的 和 旁边 的 光子 发生 干涉，  而 改变 自己 和  旁边 光子 的 运动方向  。

 

因此，   11 楼 的  单光子干涉定理  可能  不成立  。

 

也由此可知，    光 的 干涉 是 发生 在 一些 特定 的 条件 下 ，    那  光 发生 干涉  的 条件 是 什么 呢  ？

 

色散 移相 的 不同颜色 的 光 还能 合起来，  是 因为 它们 还是 “一束光”，  虽然 被利用 色散 分开 （摊平），   但 彼此间 仍然 “连成一片”，  彼此间 保持着 联系，  因此 它们 在 分开（摊平）  时，   互相之间 并不 发生 干涉，    最后 合到一起 时，  也 不 干涉   。

 

 

我以前 就 在 博客 里 提出问题  《为什么要 拿 光 的 干涉条纹 宽度 变化 作为 判断 光速 变化 的 依据 ？》

 

对于 机械波，  有 3 个 原因 都可以造成 干涉条纹 宽度 不同 ：

 

1   初始相位 差 不同

2   频率 差  不同

3   波长 差 不同

 

经过 昨天   11 楼  的 思考，   发现，     干涉 条纹 宽度 / 间隔 和  光子 的 初始相位 无关  。

 

在 色散移相  中，   可以用 路程差 来 调节 光子 初始相位 的 差距  。

 

如果  干涉条纹  和  光子 的 初始相位 有关，   那么，  光子 的 波长 是 纳米级 的，    迈克尔逊 - 莫雷 干涉仪 有 轻微的扰动，   都会 造成 光子 的  “路程差”  而 改变了 “初始相位” ， 干涉条纹 宽度 都会 发生变化  。 

 

而 事实上是，    迈克尔逊 - 莫雷 干涉仪  的 条纹 稳如泰山  。

 

双缝干涉 用的是 普通光源，  并非激光，  也就是  通过 双缝 的 两束光 是 普通光，  光子 的 初始相位 是 杂乱无章 的 ，   如果 干涉条纹 宽度 / 间隔  和 光子 初始相位 有关，   因为 光子 的 初始相位 是 杂乱无章 的，   因此 各个光子 互相 干涉 后 形成 的 条纹 也是 各种各样 的，  有 各种 宽度 / 间隔，   合起来 就是 一片模糊，  没有 明显 的 条纹  。

 

而 事实是，    双缝干涉  的 条纹 稳如泰山  。

 

因此，  初步结论是，   光 的 干涉条纹 的 宽度 / 间隔  只 和 频率 、速度 有关 ， 在 萨格纳克干涉仪 里，   光速 不一样，   干涉条纹 的 宽度 / 间隔 也不一样  。

 

干涉条纹  和 光子 的 “初始相位”  无关   。

 

光子 的  初始相位   则 是 和 光子 的 功率叠加 有关  。

 

激光 在 工作物质 里 的 谐振 是 一个 群体行为，   和 路程差 无关  。   如果 激光 的 谐振 是 靠 路程 来 调节 光子 的 初始相位 使 初始相位 对齐，   那 激光 不可能 生成  。  因为 反射镜 表面 纳米级别 的 凹凸 也会 造成 光子 的 路程差 而 导致 相位差，   一碰 反射镜，  马上 光子 的 相位 又 杂乱无章 了  。   甚至，  穿过 玻璃 时，   玻璃 表面 纳米级 的 凹凸不平，  厚薄不均，   马上 光子 的 相位 又 杂乱无章 了  。 

 

又比如 穿过透镜，   透镜 本来 就是 曲面 的，  更是 造成了 光程差 而 光子 的 相位 又 杂乱无章 了   。

 

而 事实是，   这样 不稳定 的 情形 在 现实中 从来 没出现过  。

 

色散移相 用 路程差 来 移动 初始相位 （使得 各种色光 的 相位中心 重合） 达到 谐振 的 效果，   和 激光 在  工作物质 里 的 谐振 是 不一样 的 两个 原理  。

 

一定 大小 的 工作物质  可以 承载 谐振 的 激光功率 、光子数量 是 有 极限 的 ，     而 单纯 的 增大 工作物质 可能 并不能 让 这个 极限 有效提升 。

 

色散移相 是 工程师 的 直观 、直觉 、灵感 ，   就像 电子技术 是 工程师 的 直观 、直觉 、灵感，   比如  再生 来复 超外差  。

 

最后，   本楼 又 留下了一个 问题 ：      既然 激光 的 光子 的 初始相位 的 一致（同步） 和 路程 无关，  那 怎么 色散移相 里 又 可以 把 一束 激光 用 色散  分成 各种 色光 后，  又 可以用 路程 来  调节 初始相位 了 ，   又 和 路程 有关 了  ？

 

 

 

 

 

 

 

昨天（2022-01-17）  在 构思 《展望 芯片技术》 ，   想到了 光刻机  。   既然 展望 芯片技术，  那 也要 关心一下 光刻机 的 技术 吧  。

 

为此，   我发明了 一款   萨格纳克 光刻机  。

 

 

 

 

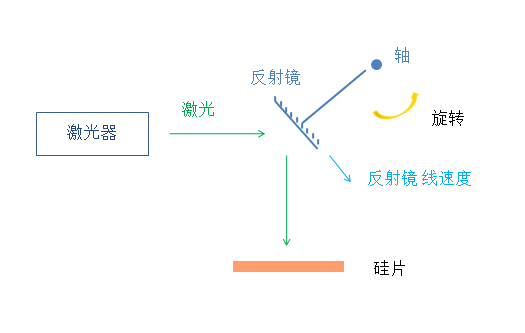
通常认为 萨格纳克 干涉仪 旋转 的 时候   干涉条纹 宽度 和 静止 时 不一样 是 因为 光速 发生了变化 。     我也是这样理解，   旋转 的 反射镜片 给 反射光 叠加了 反射镜 的 速度（分量） 。

 

上图   萨格纳克 光刻机  的 反射镜 也是 在 杆 的 带动下 围绕 轴 快速旋转，  逆时针旋转  。    当 旋转 到 图中位置  时，   激光器 发出的 激光 刚好 射在 反射镜 上，  反射 后 向下 射向  硅片  。

 

在 反射 时，   （激光）光线 被  叠加 上 反射镜 旋转 线速度 的 竖直分量，   设 反射前 的 光速 为 C， 反射镜 旋转 线速度 为 V，  V 的 水平分量 为 Vx，  竖直分量 为 Vy，  则 反射后 的 光速 为    C + Vy  。

 

C + Vy > C，    也就是 反射后 的 光速 增加了  。    在 真空中，  各种色光 光速相同，   紫光 的 波长 最短，  可知 频率 最高  。 

 

光速增大 发生 蓝移（紫移），   蓝移 意味着  光子 的 频率增加 或 波长变短，    而 又要 满足 光祖增大，   那 应该是

 

1    频率增大 波长不变

2    频率增大 波长变短

3    频率增大 波长变大

 

这 3 种情况  。

 

其实  颜色 到底 是 由 光子 频率 还是 波长 决定的，  这个还不清楚，    但 又要 满足 蓝移，  又要 满足 光速 变大，   那只能 是 上面 3 种情况，    其中  1 、3  是 颜色 由  频率 决定，   2 是 颜色 可能 由 频率 决定， 也可能 由 波长决定  。

 

其实这样 分析 还比较 粗略，   也许 颜色 是 由 频率 和 波长 联合 决定 的 呢 ？   假设 由 频率 和 波长 的 乘积 决定，  比如 越 蓝移， 频率 * 波长 越小，  这样，  紫光 的 频率 * 波长 最小，  但  频率 * 波长 是 光速，   蓝移  和 光速变大 就 矛盾了  。

 

这里 的 情况 还不明朗，   还是 从长计议  。    不过 ，   假想，    光速 变大 后，  频率增大 波长变短，   这刚好 符合我们的需要  。  波长 变短 则 “衍射极限” 更小，  甚至 “焦深” 也可以更深，  而 频率增大 也许 还能 增加 光子 的 能量 ，   这个 能量来自于哪里 ？   来自于 Vy  ？   也就是 反射镜 把 速度 的 竖直分量 Vy 叠加给 光速，  把  这部分 动能 叠加给 光子 了  ？

 

想到这里，   我们应该 开心的 笑一笑，   虽然 在 可行性 上 难度 还挺大，  因为 要求 镜片 的 转动 非常精准，  稍有偏差 则 反射 出 的 激光 的 方向 也有偏差，  就会 刻 到 硅片 上 错误的 地方  。

 

但 再想一想，   又 发现了 问题  。  假设 镜片 旋转 线速度 是  1 米 / 秒，   或者 再快一点，   Vy = 3 米 / 秒 ，   光速 C = 30 万千米 / 秒 = 3 亿 米 / 秒  ，

 

可以发现   Vy / C = 亿分之一

 

设  光 发生 干涉 的 地方 到 投影屏 的 距离 为 L，     如果  光 的 干涉条纹 的 宽度 和  L * 波长  成 正比，   L 不变，   波长变大，  则 条纹宽度 变大，  波长变小，  则 条纹宽度 变小，

 

这里 Vy / C = 亿分之一，   则 由 Vy 增加 的 光子 波长 也是 原来波长 的  亿分之一，   条纹宽度 增加 也是 原来 条纹宽度  的  亿分之一  。

 

亿分之一  的 条纹宽度 变化 微乎其微，   根本看不出来  。      但  萨格纳克 干涉仪 转动 时 条纹宽度 变化 是 显著 的  。

 

因此，    我们 上面 这套理论 好像 行不通  。

 

又想了一下，   会不会 萨格纳克 条纹宽度 变化  不是 由 光 前进方向 的 速度变化 引起的，   而是 光 前进方向 的 正交方向，也就是 “侧方向”  的 速度变化 引起 的 ？  或由 侧方向 的 速度差 产生 侧方向  的 位置差 引起 的  ？

 

速度差 还是  亿分之一  。   

 

位置差 嘛，  从 发生干涉 的 地方 到 投影屏 的 距离 为 L，   光 经过 L 的 时间 记为 t，    在 t 里，  光 向 侧边 移动 的 距离 记为 s ， 设 光 前进方向 为 竖直方向，  侧方向 为 水平方向，   s / L = Vx * t / ( C * t ) = Vx / C，   设  Vx = 3 米 / 秒  ，     s / L  =  Vx / C =  亿分之一   。

 

亿分之一  的 位置差 会不会 造成 肉眼可见 的 显著 的 干涉条纹 ？   不知道  。  而且 这个 亿分之一  的 位置差 也就是  s  是 两束光（一束光 侧向速度 为 0，  另一束光 侧向速度为 Vx） 到达  投影屏  时 在 水平方向 的 相距距离，   但 干涉条纹 是 在 起点（两束光一起出发时） 决定的，  而 不是 在 终点（到达 投影屏 时）  决定 的 吧  ？

 

其实 上面 说 反射镜 把 旋转 的 线速度 的 分量 Vx, Vy  叠加给 激光，  是  以 反射后 说的，  即 反射后 激光 变成了 竖直方向，  此时 再来 叠加 Vx, Vy 。   会不会 在 反射前 叠加 ？   或 反射前 反射后 都会 叠加 ？

 

总之，  问题 还 挺多，   这套 理论 猜想成分 也挺多，  不一定行，   但 还是 挺有 参考价值 的， 哈  。