用 CPU 计算 100 万 个 点 的 三维坐标 旋转
一次 三维旋转 由 3 次 二维旋转 组成 , 分别 是 围绕 x 轴 旋转, 围绕 y 轴 旋转, 围绕 z 轴 旋转 。 记 围绕 x 轴 、y 轴 、z 轴 旋转 的 角度 为 θx , θy , θz 。
二维平面 上 的 坐标旋转 公式
x ′ = x cos A - y sin A
y ′ = y cos A + x sin A
x ′, y ′ 为 旋转 后 的 坐标 。
根据 二维平面 上 的 坐标旋转 公式 可以 推导 出 三维坐标旋转公式, 记 旋转 后的 坐标 为 x ′, y ′, z ′ 。
先 围绕 z 轴 旋转, θz 的 基准 : x 轴 正方向 朝右, y 轴 正方向 朝上, 逆时针旋转 则 θz 为 正, 顺时针旋转 则 θz 为 负 。
x ′ = x cos θz - y sin θz
y ′ = y cos θz + x sin θz
z ′ = z (保持不变)
再 围绕 y 轴 旋转, θy 的 基准 : x 轴 正方向 朝右, z 轴 正方向 朝上, 逆时针旋转 则 θy 为 正, 顺时针旋转 则 θy 为 负 。
x ′ = ( x cos θz - y sin θz ) cos θy - z sin θy
y ′ = y cos θz + x sin θz (保持不变)
z ′ = z cos θy + ( x cos θz - y sin θz ) sin θy
再 围绕 x 轴 旋转, θx 的 基准 : y 轴 正方向 朝右, z 轴 正方向 朝上, 逆时针旋转 则 θx 为 正, 顺时针旋转 则 θx 为 负 。
x ′ = ( x cos θz - y sin θz ) cos θy - z sin θy (保持不变)
y ′ = ( y cos θz + x sin θz ) cos θx - [ z cos θy + ( x cos θz - y sin θz ) sin θy ] sin θx
z ′ = [ z cos θy + ( x cos θz - y sin θz ) sin θy ] cos θx + ( y cos θz + x sin θz ) sin θx
这个 公式 有点繁琐 。 实际在 程序里 计算时, 直接把 上次 二维旋转 后 的 x, y, z 代入 下次 旋转 计算, 这样 每次计算 都是 二维旋转, 使用的是 二维旋转 的 公式 。
项目地址 : https://github.com/kelin-xycs/PointsRotate
测试结果 :
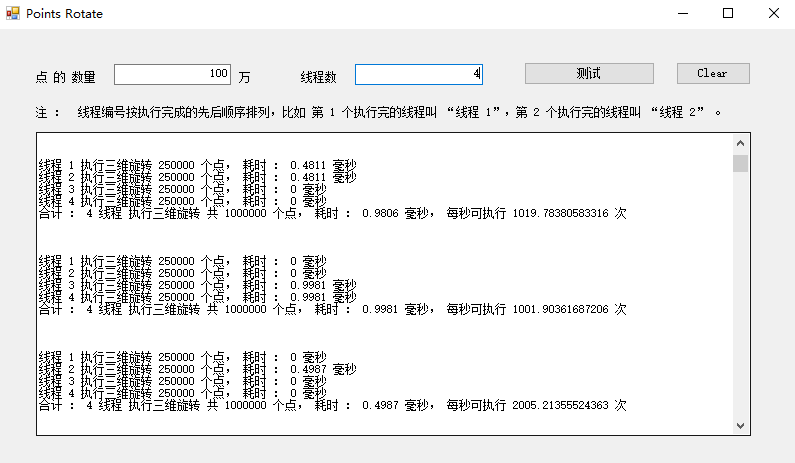


测试 的 CPU 是 2 核 4 线程, 两个 核 一个 主频 1.7 GHz, 一个 主频 2.4 GHz 。 总的来看, 2 个 线程 就可以达到 最快 了 。 其实 快慢 还跟 线程 是否 被 操作系统 安排 到 主频 高 的 那个 核 (2.4 GHz) 有关 。
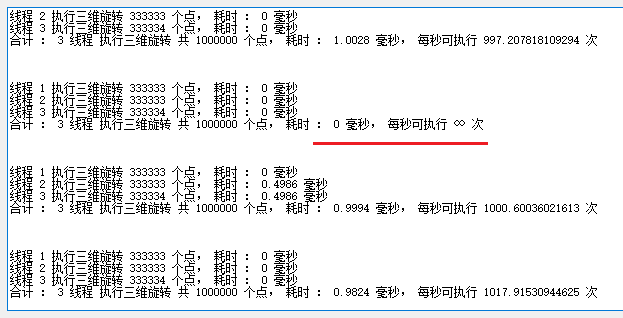
图中 红线处 可以看到, 执行速度 可以达到 每秒 无穷 次 , 其实 不是真的 无穷, 而是 执行 的 时间(毫秒数) 太小, 小于 DateTime 的 刻度, 故 按 0 毫秒 算 。 时间 为 0, 除以 0 得 无穷 。
总的来说, 1 秒 1000 次 是 没问题, 每次 旋转 100 万 个 点 。 如果 是 3D 游戏 的 话, 每一帧 旋转 100 万 个 点, 那么 可以 支持 每秒 1000 帧 。 当然 这只算了 旋转点, 没有包括 其它 工作量 。
其实 这个测试 就是 一秒 计算多少次 乘法 和 加法, 并不稀奇 。 但 如果 带了 “能不能用 CPU 多核计算 代替 FPGA / DSP / GPU” 这个问题来看, 这个 测试结果 就有 意义 了 。
第一次 测试 时, 程序 会 在 lock 块 里 创建 测试数据, 就是 100 万 个点 的 坐标, 是 一个 长度 为 100 万 的 数组 。 lock 块 可以将 这些数据 同步到 各个 核 的 Cache 。 而 测试完成 后, 测试数据 在 各个线程 所在的 核 的 Cache , 并没有再 同步, 这是 因为 计算完后, 这些 数据 是要 顺序输出, 还是 接着 在 各个核 上 继续计算, 这个是不一定的, 由 实际 的 应用 决定 。
自己编译 这个 程序 的 话, 注意用 Release 模式, 这个测试 的 Release 版本 比 Debug 版本 快 约 10 倍 。


