第九章 代数系统
9.1 二元运算及其性质
定义：设集合S，有函数f：SxS→S 称为S上的二元运算。
注意标红，运算体现了封闭性：集合里的元素运算结果还是集合里的元素。这里举个栗子：
自然数集的加法运算是二元运算：
一个自然数N加上另一个自然数N的结果还是自然数；
而减法运算则不是二元运算：
2 - 5 = -3，-3不是自然数。
运算表：
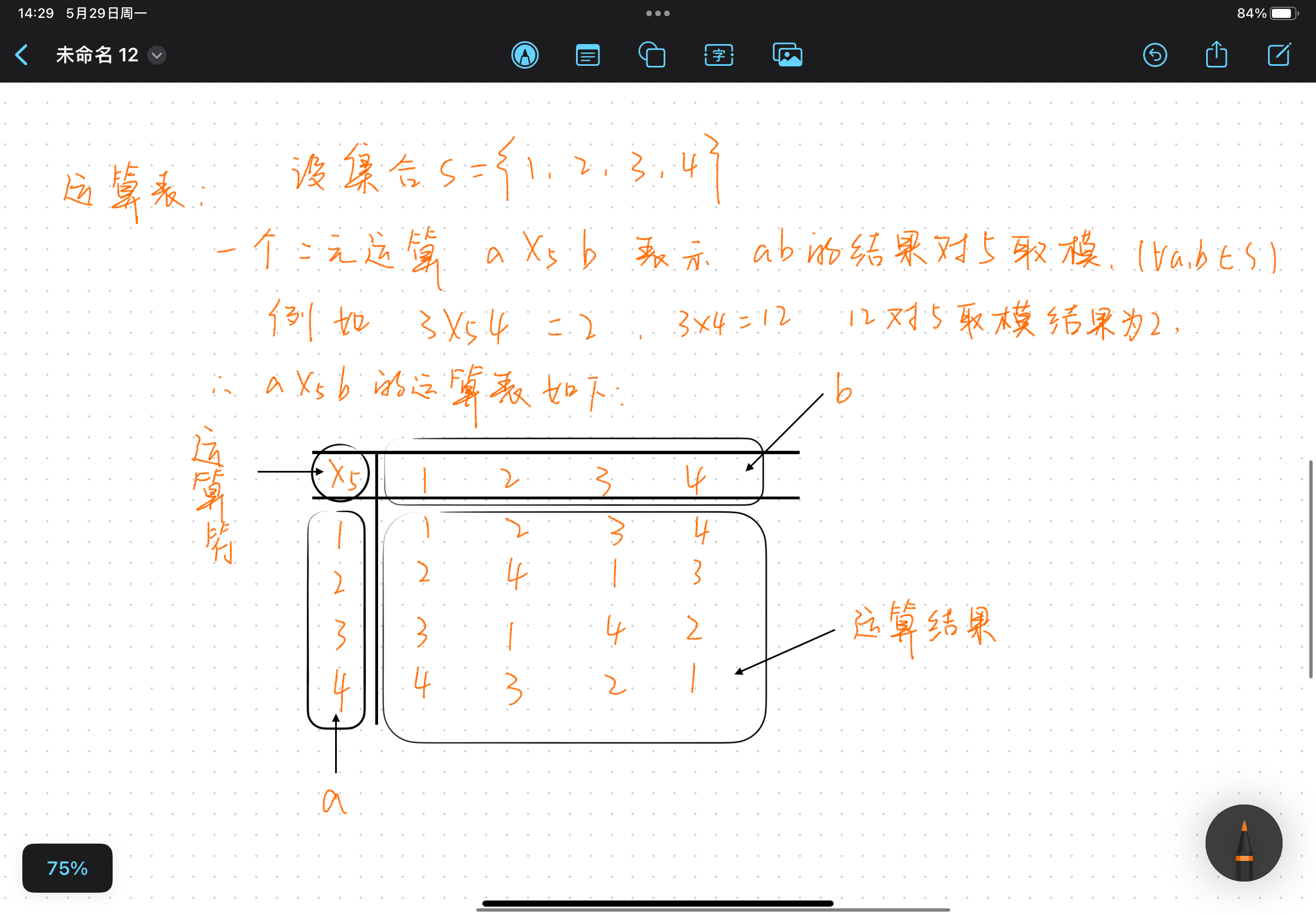
由上述运算表我们可以分析得出运算律：
交换律：
若a X5 b = b X5 a，则说运算X5在S上是可交换的，即满足交换律。
结合律：
若 （a X5 b）X5 c = a X5（b X5 c），则说运算X5在S上是可结合的，即满足结合律。
幂等律：
若a X5 a = a，则说运算X5 适合幂等律，此时a被称作幂等元。
例如上图运算表中 1 X5 1 = 1，此时1被称作幂等元。
分配律和吸收律是对两个二元运算来说的。
分配律：
这里我们拿小学二年级就学过的加法和乘法来举例，通过类比对其它运算也得出相应的结论：
在自然数N集合中，有
a×（b + c）=（a×b）+（b×c）则说运算满足左分配律；
（a + b）× c =（a×c）+（b×c）则说运算满足右分配律。
如果同时满足左右分配律则说乘法（×）运算对加法（+）运算满足分配律。这里不能说加法（+）对乘法（×）满足分配律，因为交换位置后不难发现运算不可分配了。
吸收律：
设一个集合S上二元运算#和@，
若对任意x,y∈S，都有x @ ( x # y ) = x # ( x @ y ) = x，则称运算@与#在S上满足吸收律。举例：∩和∪运算。
由这个例子我们还可以延伸出单位元和逆元：
单位元：
很好理解，一个二元运算中的一个元素与另一个元素运算后的结果是它本身，则称该元素为单位元，或者幺元。单位元运算分左右。例如上述X5运算：
1 X5 a = a，a为集合S的任意元素，我们说1是X5运算的幺元。这个从上面的运算表中不难看出。
逆元：
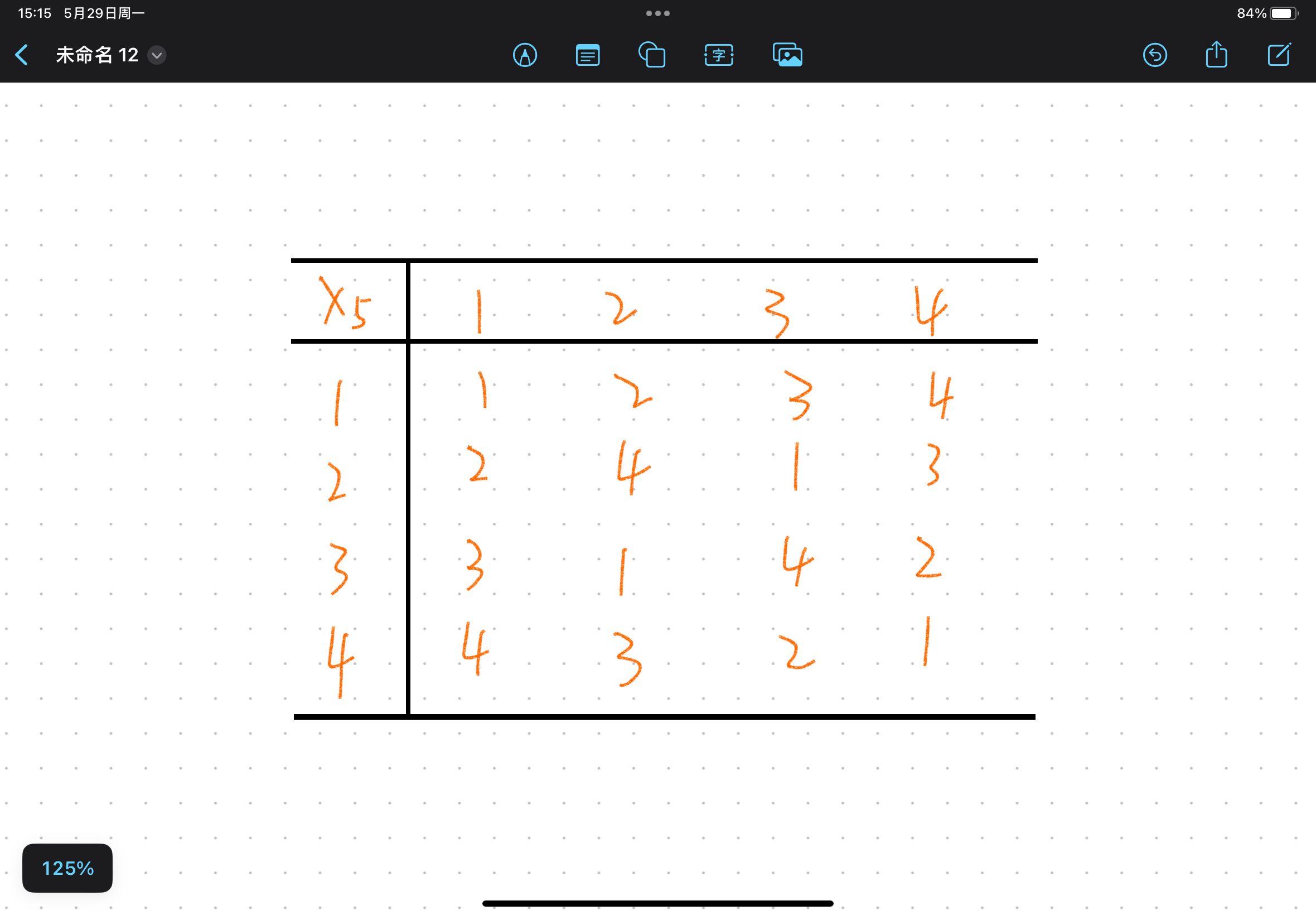
也很好理解，类似于数乘运算中的倒数。一个元素与另一个元素的二元运算得到的结果是单位元，则称该元素是另一元素的逆元，逆元也分左右。在上图运算表中，我们来找逆元：
由于1是单位元，所以我们找：
2 X5 3 = 1 3 X5 2 = 1 4 X5 4 = 1 1 X5 1 = 1
2的逆元是3，3的逆元是2，4的逆元是4，1的逆元是1
而零元也相当好理解：
零元：
整数集合的数乘运算中，我们知道0乘任何数都是0，也就是说在该二元运算中，0对该集合中任意元素的运算结果都是0，这就是零元的性质。用数学符号来写就是0×a = 0，其中a∈Z。
由零元我们可以再增加一个运算定律：
消去律：
若对任意x,y,z∈S，都有x@y=x@z 且y@x=z@x 且x不是零元，满足y=z，此时称@满足消去律。
第十章 群与环
10.1 群的定义及性质
我们可以简单理解群的定义半群，幺半群和群三者是层层递进的关系，半群给定特定条件后可以变为幺半群，幺半群再给定特定条件可以变成群。半群就是当代数系统的二元运算是可结合的，便可称代数系统为半群。只需要满足代数系统二元运算可结合就行。
如果半群对二元运算存在单位元（幺元），那么半群就变成了幺半群。这个幺就是单位元的意思。
如果幺半群里所有的元都有其逆元与之对应，那么称该幺半群为群。
这里有一个四元群的概念：
Klein四元群：具有特征：
- 存在单位元；
- 群的运算满足交换律；
- 每个元素的逆元是它本身；
- 任意两元素运算结果是第三个数
的群就是Klein（克莱因）群。
定义：
- 若群G是有穷集，则称G为有限集，否则称作无限群。群的基数称为群的阶。
- 只含单位元的群称为平凡群。
- 若群中的二元运算是可交换的，则称G为交换群或阿贝尔（Abel）群。
这里的有穷指的是群中的元素是有限个的，可以很多，但一定是有限的。群的基数则是群的元素的个数。
定义：
某元素的阶（注意不是群的阶），也称为周期，可以如图理解：
10.2 子群与群的陪集分解
书上有一句很精炼的话：子群就是群的子代数。
这里我认为可以类比集合来理解，集合中有子集，子集被包含于其“父集”中，而子群也是群的一部分。但是子群的要求更高：子群也得满足群的性质，
子群和真子群的理解类比子集和真子集，这里还有一个平凡子群的内容。说到平凡，都离不开单位元这一概念，包括后面的图，有一个叫做平凡图的图，只有点没有边，这里后面再说。平凡子群就是只含幺元的子群或该群本身。也就是说一个群的平凡子群有两个：1. 只含幺元的群；2. 群G本身。
之后是子群的三个判定定理：
看着很复杂，其实要证子群就从两个点入手，一是证明充分性，二是必要性。分点证明后得出结论即可。
（没完，后面的等有时间再补，主要是子群格和陪集）
（有错误可指出，虚心接受意见）
