离散数学第二版（屈婉玲）第二部分内容总结

第二部分 集合论 总结

第6章 集合代数

　　6.1 集合的基本概念

　　集合中的关系：

　　　　元素和集合之间：属于或不属于。

　　　　集合与集合之间：包含被包含，子集，真子集，空集，幂集。

 

　　6.2 集合的运算

　　集合的基本运算：

　　　　并、交、相对补、对称差、绝对补

 

　　　　VN图（文氏图）表示：

 

　　6.3 有穷集的计数

　　包含排斥原理：

　　　　书上一个很经典也很能体现包含排斥原理的例子：

　　（例子图）

 

　　包含排除原理很好解这种满足多条件（性质），条件（性质会重叠的解问题，先找出全集的所有元素，再将每个元素满足一个条件（性质）元素个数找出，再将满足两个条件（性质）元素个数找出，以此类推做差求和求解。

 

　　6.4 集合恒等式

　　集合恒等式有很多，其中我认为会比较常用的且比较基础的有交换律、结合律、分配律、同一律、零律、吸收律和德摩根律。以下为书上的主要算律展示：

（附图片）

 

 

 

 

 

 

 

第7章 二元关系

　　7.1 有序对与笛卡儿积

　　有序对（序偶）定义：

　　由两个元素x和y（允许x=y）按照一定顺序排列成的二元组。说人话就是：

　　　　<x, y> 长这样，x是第一元素，因为它在前面；y是第二元素。

　　有序对<x, y> 性质：

　　　　简单地说：

　　　　　　1. 当x != y，<x, y> != <y, x>

　　　　　　2. <x, y> = <u, v> 充要条件是x=u，y=v

　　笛卡儿积：

　　　　人话：

　　　　　　设A = {a, b}，B = {0, 1, 2}

　　　　　　A X B = { <a, 0>,  <a, 1>,  <a, 2>,  <b, 0>,  <b, 1>  <b, 2> }

　　观察规律发现用A中的元素作为第一元素与B中元素作为第二元素的所有结果。所以这样就会有一个性质：A X B != B X A。B X A 则应当将A X B 中的每个序偶调换第一和第二元素。这个性质的前提是A，B都不为空集且A与B不相等。而由前提又可以得出另一个性质：

对任意集合A，有 A X ∅= ∅

7.2 二元关系

二元关系满足条件：

1. 1. 集合非空，且它的元素都是有序对（序偶）；

例如：{<x, y>,<y, z>}是有序对，{<x, y>, z}不是有序对。

　　　　　　2. 集合是空集；

 

书上的二元关系：

E_A : 定义A上的全域关系，其中元素满足 E_A  = A X A

I_A ：定义A上的恒等关系，其中元素满足  I_A = {<x, x>|x∈A}

LA：定义A上的小于等于关系，其中元素满足 LA = {<x, y>|x<=y}

DA：定义A上的整除关系，大体同上，字面意思理解，a|b的意思是b能被a整除，如2|4 表示4能被2整除

R_⊆：定义A上的包含关系，可能比较难理解，这里举例：A中的元素有例如：{∅{a}, {b}, {a,b}}, 则R_⊆中的一个元素长这样：<{a}, {a,b}> 第一元素被包含于第二元素，或者说第二元素包含第一元素，这就是包含关系。特殊地，如果包含关系内有空集，则空集被包含于所有元素（包括空集本身）

 

关系矩阵：

　　话不多说，直接上图：

 

 

关系图：

　　上图：

 

 

 

7.3 关系的运算

三种域：

　　定义域与值域和域：

　　还是上图（狠狠地爱上上图了，家人们谁懂啊（乐））：

 

 

 

逆关系：

不用多说，直接理解：

R^-1  = {<x, y>|<y, x> ∈R}，就这样

右复合：

很像后面要说的传递关系：

 

 

G对F的右复合，记作F  G = {<x, y>|∃t(<x, t> ∈F⋀<t, y> ∈G)}

关系的次幂：

挺有意思的，书上是这样写的：

 

 

其中，I_A是恒等关系，就是里面的第一元素与第二元素相等。I_A 的关系矩阵毫无疑问是单位阵，可以试试通过上面的方法来动手写一下I_A 的关系矩阵

我们可以通过关系矩阵的次幂的运算得知关系的次幂的关系，这么说可能有点绕，那么上图：

 

 

可以看出，M⁴ 之后的运算会进入循环，以此类推得出R²以后的运算会进入循环。

 

7.4 关系的性质

自反和反自反：

说人话，看图：

 

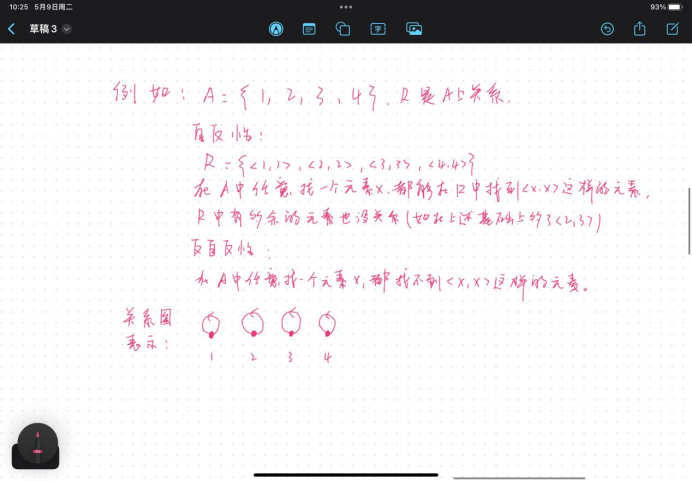
对称和反对称：

 

 

传递：

 

 

 

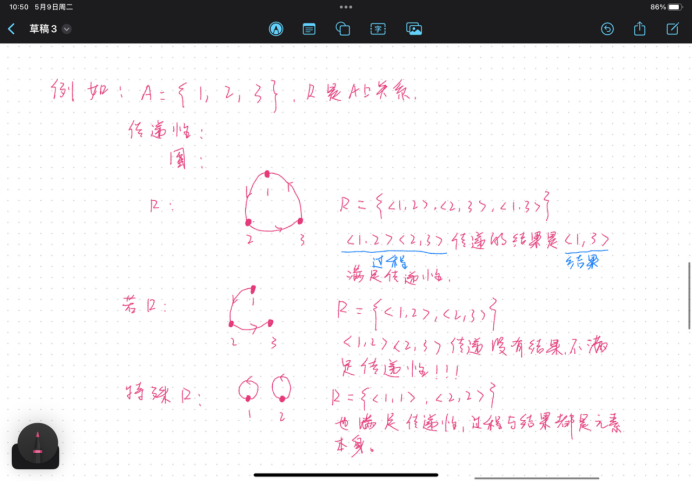
7.5 关系的闭包

主要是Warshall算法，这里跳过，网上各路大神都有很好的讲解，自己理解并不是很到位，这里不细讲。

 

7.6 等价关系与划分

等价关系：

一个很好的例子：

 

 

自反性：<0，0>  <1，1>  <2，2>  <4，4> 等

对称性：<0，4>  <4，0>  <0，8>  <8，0> 等

传递性：<0，4>  <4，8>  <1，5>  <5，9> 等

三种性质都满足，所以R是A上的等价关系。

要证明等价关系，则要从三种性质入手，分别证明满足三种性质，最后得到等价关系的结论。

 

商集的定义：

 

 

 

划分与划分块：

 

 

由图可知，划分就是大圆，划分块就是大圆里被线分割的块块。类似于分蛋糕。

7.7 偏序关系：

偏序关系的定义：

 

 

图截自百度，比书上简洁。

 

两个例子：

 

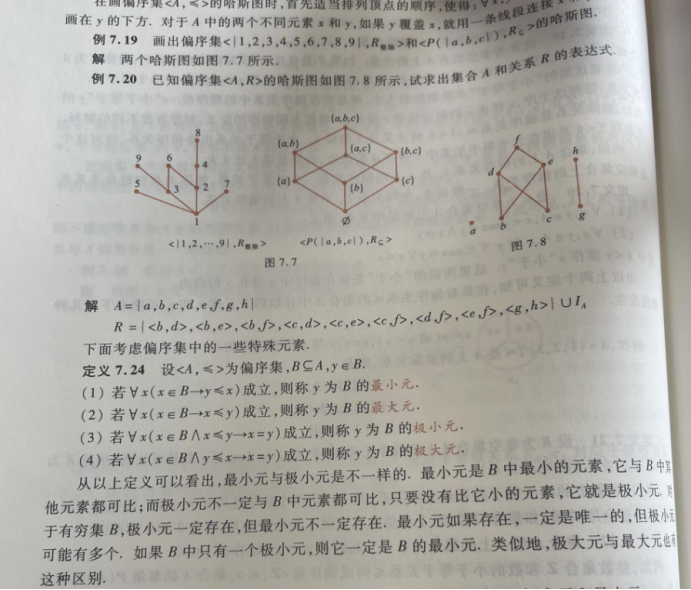
通过图7.8我们可以分析出极小元，极大元，最小元和最大元。

　　如图：

1. 1. a是孤立点，所以它既是极小元也是极大元。
   2. 其它极小元：b，c，g；其它极大元：f，h。
   3. 没有最小元与最大元，因为这两个都是唯一的。如果把图中h去掉，就会有f是最大元，g成了孤立点；再将c去掉就得到b是最小元。

再来：

 

所以没事儿多看书，书上有的东西说的也挺明白的。