BZOJ 4176 Lucas的数论 莫比乌斯反演+杜教筛
题意概述：求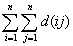
，n<=10^9，其中d(n)表示n的约数个数。
分析：
首先想要快速计算上面的柿子就要先把d(ij)表示出来，有个神奇的结论：
证明：当且仅当a,b没有相同的质因数的时候我们统计其贡献，可以发现所有被统计的(a,b)乘积的质因数分解形式正好和i,j的所有因数的质因数分解形式一一对应，不重不漏（对于b中质因数指数不为0对应的就是i中指数+b中指数的情况，对于b中质因数指数为0的情况对应i中指数的情况）。
然后就有如下的推导：
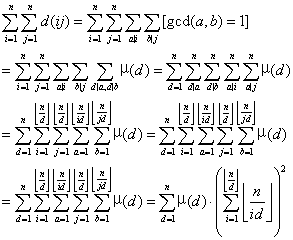
对于这个式子，整个数字分段来算，n/d一共sqrt(n)种取值，用杜教筛求μ的前缀和，后面那部分每次可以用sqrt(n/d)的复杂度计算出来，整个时间复杂度大约是O(n^(3/4))。（实在是太玄学了这个时间复杂度我不是很会算ORZ）
至于杜教筛......这里我就不讲了吧，看dalao链接！：http://jiruyi910387714.is-programmer.com/posts/195270.html
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<queue> 8 #include<set> 9 #include<map> 10 #include<vector> 11 #include<cctype> 12 using namespace std; 13 const int mo=1000000007; 14 const int maxn=1000005; 15 16 int N,pri[maxn],mu[maxn],tot; 17 bool ntp[maxn]; 18 struct Hash{ 19 static const int sz=3000007; 20 static const int maxn=10000005; 21 int first[sz],np,next[maxn],id[maxn],val[maxn]; 22 Hash(){ 23 np=0; 24 memset(first,0,sizeof(first)); 25 } 26 void ins(int pos,int v){ 27 int i=pos%sz; 28 next[++np]=first[i],first[i]=np; 29 id[np]=pos,val[np]=v; 30 } 31 int query(int pos){ 32 int i=pos%sz; 33 for(int p=first[i];p;p=next[p]) 34 if(id[p]==pos) return val[p]; 35 return -1; 36 } 37 }hash; 38 39 void get_mu() 40 { 41 ntp[0]=ntp[1]=1,mu[1]=1; 42 for(int i=2;i<=1000000;i++){ 43 if(!ntp[i]) pri[++tot]=i,mu[i]=-1; 44 for(int j=1;j<=tot&&1ll*pri[j]*i<=1000000;j++){ 45 ntp[i*pri[j]]=1; 46 if(i%pri[j]==0){ mu[pri[j]*i]=0; break; } 47 mu[pri[j]*i]=-mu[i]; 48 } 49 } 50 } 51 int F(int n){ 52 int re=0; 53 for(int i=1,last;i<=n;i=last+1) 54 last=n/(n/i),re=(re+1ll*(last-i+1)*(n/i)%mo)%mo; 55 return re; 56 } 57 int S(int n){ 58 int re=hash.query(n); 59 if(re!=-1) return re; 60 re=1; 61 for(int i=2,last;i<=n;i=last+1){ 62 last=n/(n/i); 63 re=(re-1ll*(last-i+1)*S(n/i)%mo+mo)%mo; 64 } 65 hash.ins(n,re); 66 return re; 67 } 68 int solve(int n) 69 { 70 int re=0,f; 71 for(int i=1,last;i<=n;i=last+1){ 72 last=n/(n/i),f=F(n/i); 73 re=(re+1ll*f*f%mo*(S(last)-S(i-1)+mo)%mo)%mo; 74 } 75 return re; 76 } 77 int main() 78 { 79 get_mu(); 80 int sum=0; 81 for(int i=0;i<=1000000;i++) 82 hash.ins(i,sum=(sum+mu[i]+mo)%mo); 83 scanf("%d",&N); 84 printf("%d\n",solve(N)); 85 return 0; 86 }
