计量经济学/吴恩达课程笔记_4-1~4-4_关于特征缩放法的一些疑问和理解
吴佬在多元线性回归之后, 补充了特征缩放法的优化, 有一些疑问,现在一一解决
- 为什么在一元的时候不需要,而多元的时候需要?
- 特征缩放法本质是在对已有样本特征做什么过程?
- 为什么特征缩放法能够优化?优化在哪里呢?
- 有哪些特征缩放法?分别有什么特点?
因为个人水平不足, 解释不足够严谨,并没有系统证明,帮助理解耳
为什么在一元的时候不需要,而多元的时候需要?
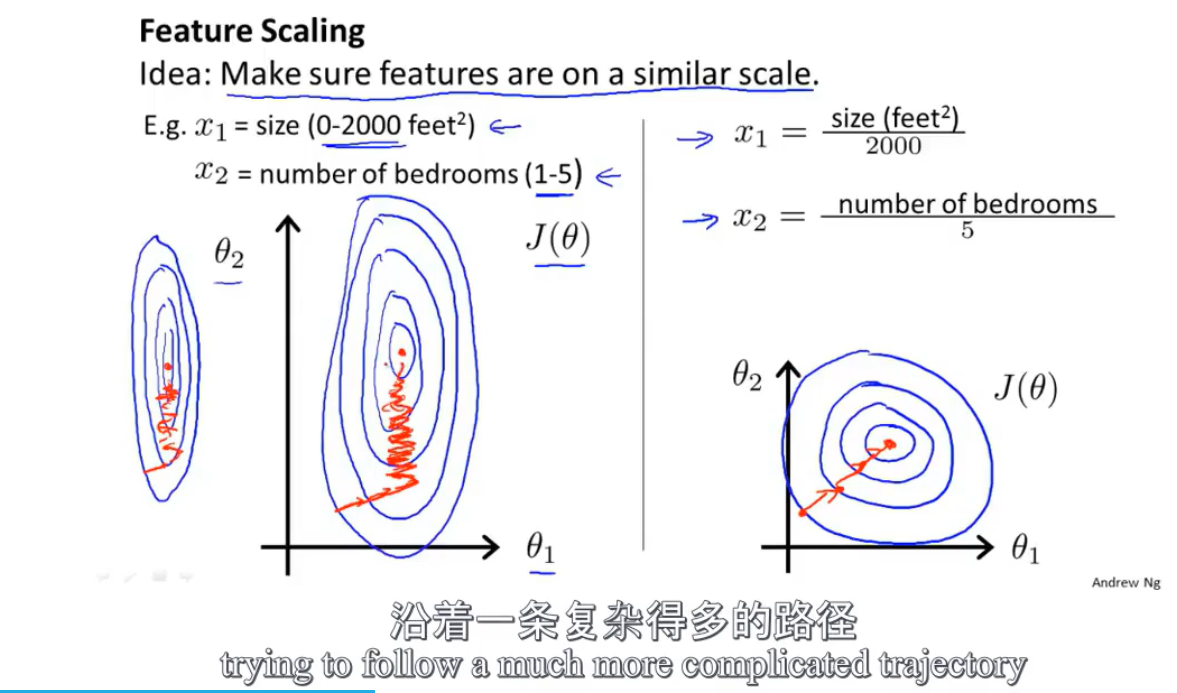
第一个问题, 吴佬给了两张等高线图,
他说,当不同方向上的的特征范围差的很远的时候, 这个下山找极点的过程,路径会变得非常复杂,会呈现如图不断振荡的路径
如果不缩放, 找极点的过程会走很多弯路,为什么会这样呢?
对于如图情况, 下山每一步可以写成:
J=a1(0e/0Θ1)+a2(0e/0Θ2) (0e/0Θ)=1/2m*sigma(y-yi)xi 直到梯度收敛=0
其中e为山的高度,也就是残差平方和==代价函数
我们先假设x1,x2是在各自区间间隔, 相同的一系列样本, 总共有k组样本
x1的尺度=400/k,x2的尺度=1/k. 画在等高线上, 各自的参数每移动一个单位, 偏移量之比就是400/1 ,
在Θ2~Θ1的等高线图, 移步 单位偏移量/偏移量尺度 之比=Θ2/Θ1=1/400,斜率=1/400
所以每次移动的方向都是如图 |斜率|=1/400 的那种移动方式.
不断地在一定范围内交叉步伐,形成震荡的路径, 寻找 梯度 收敛的过程变成一种曲折的过程
一元的时候只有一个参数方向上会偏移, 不存在两种不同偏移量不规则的情形所以不需要
特征缩放法本质是在对已有样本特征做什么过程?
特征缩放法本质就是在使偏移量能够规则, 或者说规范化, 使不同欲求参数对应的样本~实参尺度一样
为什么特征缩放法能够优化?优化在哪里呢?
不同参数对应的样本系数x1x2线性无关,所以互不干扰
特征缩放改变偏移量, 但是不会改变极点的相对位置,只是使得查找路径更规则而不是曲折进行
这也可以理解成为一种均值归一化, 或者标准化的过程(概统里面把不规则正态分布化成标准正态分布的过程也叫标准化)
这样少走弯路, 少几次迭代,使收敛的更快
有哪些特征缩放法?分别有什么特点?
https://blog.csdn.net/u011984148/article/details/99440115
计量经济学中对缩放数据介绍





