计量经济学/吴恩达课程笔记_2-1~2-7_一元线性回归/最小二乘法_公式推导
看视频之前,先回忆对回归的理解:
一元线性回归其实就是对一个自变量,一个因变量,
我们期望有 y= a+bx ,作为它们的关系式,能够解释x和y之间的关系,
已知一组(x,y)1-n,现在根据这个已知的条件,
- 关系式系数——是否一定存在?
- 若存在,a,b,最有可能是什么?
在吴恩达的课程里,详细讨论了第二个问题,最有可能,
最正确的a,b取值,就是 |a*xi+b-yi-y| =>(a*xi+b-yi-y)^(2)(实际值)最小的,即偏离程度最小,所以又叫,离差,或者,残差(残余量)
由于有多个样本,所以我们求的是 sigma (a*xi+b-yi)的,这就是计量经济学里说的残差平方和的方程,或者说函数,又叫代价函数, 名字太多了...
给出, f(a,b)=(1/2n)*sigma (a*xi+b-yi),
为什么*1/2*n? (这里现在还有点模糊,不是很确定)
我猜是为了使残差标准化? n代表n项,1/2代表, 两种不同的偏离方向, 更大,或者更小,残差为正或负?
或者,也有可能是一个中心值? 相当于一个期望值?
求f(a,b)最小值, 实际上就是求函数极小值的最小值,
吴佬在这里讲的非常详细,他说确定这个最小值的过程,求极值的过程,就是一个使沿着梯度探索的过程,我希望不断下山走到最底
随便找一个点, 梯度一开始先很高, 移步一次下降得很快,但是越靠近极值处,梯度越小, 移步一次下降的越慢, 最后到极值时,梯度=0;
这个不断移步过程, 梯度不断变小, 或者说下降的过程 ,概括一下, 就叫"移步梯度下降法",
更简洁一点--又叫作 -- 梯度下降法.
那写成代码就是,

往 a,b 两个方向都能移步,每次移步了之后从f1位置变到f2,就要更新出发点为f2,下次从f2出发, 不断重复,就是不断迭代
而梯度越来越小, 实际上也就是导数越来越小趋近于0,负数不行,
所以除了导函数为0, 又可以进一步用导函数的导数----二阶导来判定,
所以f(a,b)=(1/2n)*sigma (a*xi+b-yi),当f(a,b)=min(f(a,b)),此时的a,b为我们所需要的最有可能满足关系式ax+b的参数值
按照吴老一开始说的,这就是一个"最小化"过程.
求导,令导数为0,得到表达式;
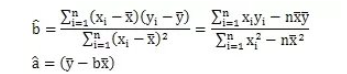
其中一种表达式的证明:
求偏导数 二阶导判定极值存在性---其实这也是5个基本假定其中的样本变异性
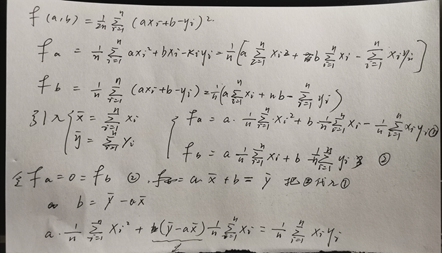
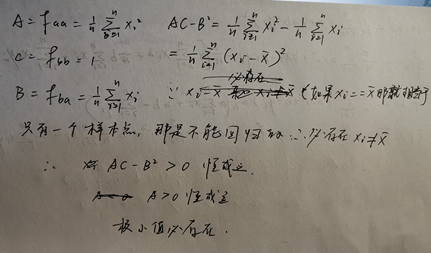
化简公式:
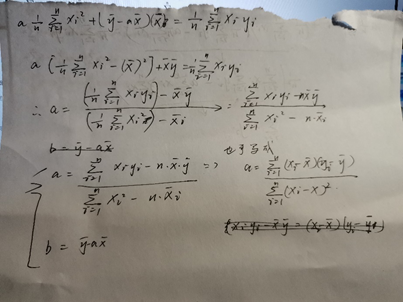
另一种表达式的推导, 更详细的:
https://blog.csdn.net/weixin_38278993/article/details/100556051






