【机器学习】通过正则化解决过拟合问题

 过拟合问题的表现：

在之前的线性回归问题中，我们通过拟合一条曲线来预测新的样例，在这条直线拟合的过程中，可能会出现欠拟合或过拟合现象，如图所示1是欠拟合，2是过拟合：

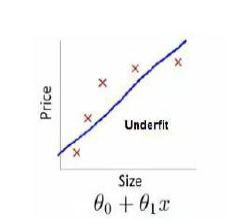
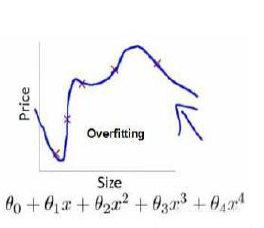
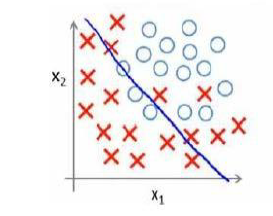
过拟合问题往往表现为虽然图像经过了所有的点，但是函数仍然存在波动，即不稳定平滑。

过拟合通常伴随着高方差，导致不能应用到新的数据中去。

过拟合产生的原因：

数据样本过少或者参数特征过多

过拟合问题的解决方法：

1）减少样本中特征变量的种类数量

2）正则化

正则化

一颗正则化的栗子：

在之前的线性回归问题中，我们的假设函数是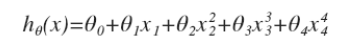这个函数中，那些高次项就是导致过拟合的原因，所以如果我们能够让那些高次项变小，那么就可以很好的拟合。

如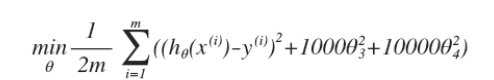，通过这样的代价函数我们就可以减少θ3，θ4对假设函数的影响，这样就引入一个较为广泛的假设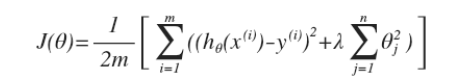

经过对较高次参数的惩罚，有助于使得函数的参数值较小，所对应的函数月光滑简单。

其中λ是正则化参数，根据管理，我们不对θ0进行惩罚。在λ的选取上，如果λ过大，会吧所有的参数都最小化，导致h（x） = θ0，即会欠拟合，如图所示分别为之前过拟合的情况，正则化之后的情况，λ过大，欠拟合的情况

 

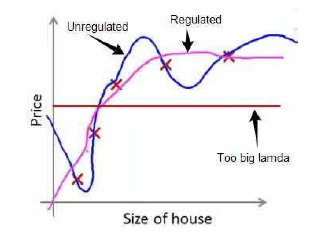
我们所增加的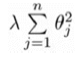，如果λ很大的话，为了使cost尽可能的小，所有的θ值（除θ0）都会在一定程度上减小，那么θ1+都会趋近于0，所得到的就是一条直线了，因此对于正则化，我们需要选取一个适合的λ，才能更好的正则化。

正则化在线性回归中的实现：

 如果我们要使得代价函数最小化，我们又不对θ0进行正则化，所以这时梯度下降算法又分为以下两种情形

 

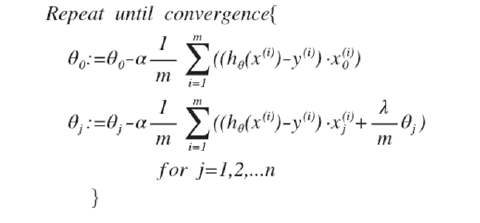
这时我们对上面的算式进行合并，就可以得到新的θJ

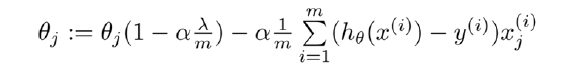
可以看出，正则化线性回归的梯度下降算法变化在于，每次在原有的算法更新的基础上，让θ减少一个额外的值。式中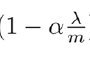使得θj的平方范数减小。

 

此方法同样可以用于正规方程求解线性回归模型中：

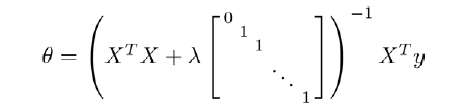矩阵的尺寸为(n+1)^2

 

正则化在逻辑回归中的实现：

 在逻辑回归中，我们同样的给代价函数增加一个新的正则化表达式，得到

要使得最小化该代价函数，通过求导，得出梯度下降算法：

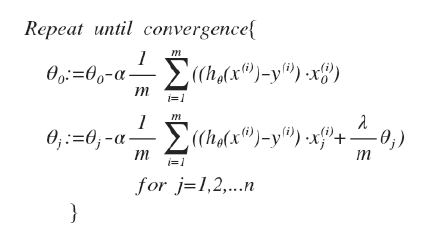
在形式上，与线性回归类似，但是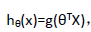所以并不和线性回归一致。

在octave中，我们依然可以通过fminuc函数来求解代价函数的最小化参数，但是，参数θ0的更新规则与其它情况不同。