【51NOD】1006 最长公共子序列Lcs(动态规划)
给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的)。
比如两个串为:
abcicba
abdkscab
ab是两个串的子序列,abc也是,abca也是,其中abca是这两个字符串最长的子序列。
Input
第1行:字符串A 第2行:字符串B (A,B的长度 <= 1000)
Output
输出最长的子序列,如果有多个,随意输出1个。
Input示例
abcicba abdkscab
Output示例
abca
问题定义
• 子序列
– X=(A, B, C, B, D, B)
– Z=(B, C, D, B)是X的子序例
– W=(B, D, A)不是X的子序例
• 公共子序列
–Z是序列X与Y的公共子序列如果Z是X的
子序也是Y的子序列。
最长公共子序列(LCS)问题
输入:X = (x1,x2,...,xn),Y =
(y1,y2,...ym)
输出:Z = X与Y的最长公共子序
列
最长公共子序列结构分析
• 第i前缀
– 设X=(x1, x2, ..., xn)是一个序列,X的第i前
缀Xi
是一个序列,定义为Xi=(x1, ..., xi )
例. X=(A, B, D, C, A), X1=(A), X2=(A, B), X3=(A,
B, D)
优化子结构
定理1(优化子结构)设X=(x1, ..., xm)、
Y=(y1, ..., yn) 是两个序列,Z=(z1, ..., zk)是X与Y的
LCS,我们有:
⑴ 如果xm=yn, 则zk=xm=yn, Zk-1
是Xm-1
和Yn-1
的
LCS,即,LCSXY = LCSXm-1Yn-1
+ <xm=yn>.
⑵ 如果xm.yn
,且zk.xm
,则Z是Xm-1
和Y的
LCS,即 LCSXY= LCSXm-1Y
⑶ 如果xm.yn,且zk.yn,则Z是X与Yn-1
的LCS,
即 LCSXY= LCSXYn-1
证明:
⑴. X=<x1, …, xm-1, xm>, Y=<y1, …, yn-1, xm>,则
LCSXY = LCSXm-1Yn-1
+ <xm=yn>.
设zkxm
,则可加xm=yn
到Z,得到一个长为k+1的
X与Y的公共序列,与Z是X和Y的LCS矛盾。于是
zk=xm=yn
。
现在证明Zk-1
是Xm-1
与Yn-1
的LCS。显然Zk-1
是Xm-
1
与Yn-1
的公共序列。我们需要证明Zk-1
是LCS。
设不然,则存在Xm-1
与Yn-1
的公共子序列W,W
的长大于k-1。增加xm=yn
到W,我们得到一个长
大于k的X与Y的公共序列,与Z是LCS矛盾。于
是,Zk-1
是Xm-1
与Yn-1
的LCS.
⑵ X=<x1, …, xm-1, xm>, Y=<y1, …, yn-1, yn>,
xmyn
,zkxm
,则 LCSXY= LCSXm-1Y
由于zkxm
,Z是Xm-1
与Y的公共子序列。我
们来证Z是Xm-1
与Y的LCS。设Xm-1
与Y有一
个公共子序列W,W的长大于k, 则W也是X
与Y 的公共子序列,与Z是LCS矛盾。
⑶ 同⑵可证。
X和Y的LCS的优化解结构为
LCSXY=LCSXm-1Yn-1
+ <xm=yn> if xm=yn
LCSXY=LCSXm-1Y if xm≠yn, zk≠xm
LCSXY=LCSXYn-1 if xm≠yn, zk≠yn

建立LCS长度的递归方程
• C[i, j] = Xi与Yj 的LCS的长度
• LCS长度的递归方程
C[i, j] = 0 if i=0 或 j=0
C[i, j] = C[i-1, j-1] + 1 if i, j>0 且 xi = yj
C[i, j] = Max(C[i, j-1], C[i-1, j]) if i, j>0 且 xi ≠ yj
自底向上计算LCS的长度
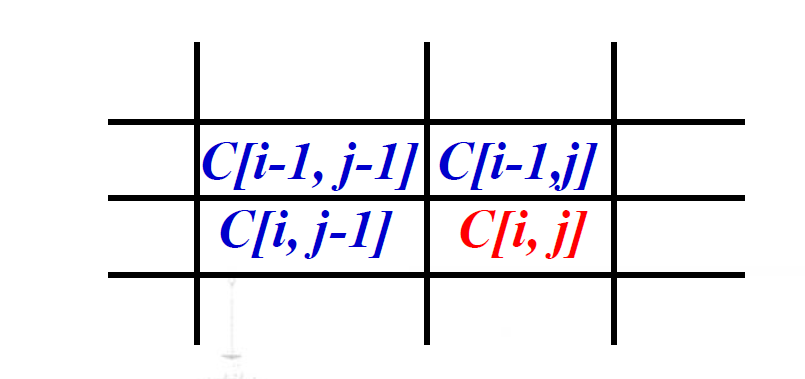

计算LCS长度的算法
– 数据结构
C[0:m,0:n]: C[i,j]是Xi
与Yj
的LCS的长度
B[1:m,1:n]: B[i,j] 是指针, 指向计算
C[i,j]时所选择的子问题的优化解所对
应的C表的表项
LCS-length(X, Y)
m←length(X);n←length(Y);
For i←1 To m Do C[i,0]←0;
For j←1 To n Do C[0,j]←0;
For i←1 To m Do
For j←1 To n Do
If xi = yj
Then C[i,j]←C[i-1,j-1]+1;B[i,j]←“↖”;
Else If C[i-1,j]≥C[i,j-1]
Then C[i,j]≥C[i-1,j]; B[i,j]←“↑”;
Else C[i,j]≥C[i,j-1]; B[i,j]←“←”;
Return C and B.
构造优化解
• 基本思想
– 从B[m, n]开始按指针搜索
– 若B[i, j]=“↖”,则xi=yj
是LCS的一个元
素
– 如此找到的“LCS”是X与Y的LCS
Print-LCS(B, X, i, j)
IF i=0 or j=0 THEN Return;
IF B[i, j]=“↖”
THEN Print-LCS(B, X, i-1, j-1);
Print xi;
ELSE If B[i, j]=“↑”
THEN Print-LCS(B, X, i-1, j);
ELSE Print-LCS(B, X, i, j-1).
Print-LCS(B, X, length(X), length(Y))
可打印出X与Y的LCS。
1 /*功能:计算最优值 2 *参数: 3 * x:字符串x X:字符串x最大长度 4 * y:字符串y Y:字符串y最大长度 5 * b:标志数组 6 * xlen:字符串x的长度 7 * ylen:字符串y的长度 8 *返回值:最长公共子序列的长度 9 * 10 */ 11 int Lcs_Length(string x, string y, int b[][Y+1],int xlen,int ylen) 12 { 13 int i = 0; 14 int j = 0; 15 16 int c[X+1][Y+1]; 17 for (i = 0; i<=xlen; i++) 18 { 19 c[i][0]=0; 20 } 21 for (i = 0; i <= ylen; i++ ) 22 { 23 c[0][i]=0; 24 } 25 for (i = 1; i <= xlen; i++) 26 { 27 28 for (j = 1; j <= ylen; j++) 29 { 30 if (x[i - 1] == y[j - 1]) 31 { 32 c[i][j] = c[i-1][j-1]+1; 33 b[i][j] = 1; 34 } 35 else 36 if (c[i-1][j] > c[i][j-1]) 37 { 38 c[i][j] = c[i-1][j]; 39 b[i][j] = 2; 40 } 41 else 42 if(c[i-1][j] <= c[i][j-1]) 43 { 44 c[i][j] = c[i][j-1]; 45 b[i][j] = 3; 46 } 47 48 } 49 } 50 51 cout << "计算最优值效果图如下所示:" << endl; 52 for(i = 1; i <= xlen; i++) 53 { 54 for(j = 1; j < ylen; j++) 55 { 56 cout << c[i][j] << " "; 57 } 58 cout << endl; 59 } 60 61 return c[xlen][ylen]; 62 }
完整代码
//只能打印一个最长公共子序列
#include <iostream>
using namespace std;
const int X = 1000, Y = 1000; //串的最大长度
char result[X+1]; //用于保存结果
int count=0; //用于保存公共最长公共子串的个数
int c[X+1][Y+1];
int b[X + 1][Y + 1];
/*功能:计算最优值
*参数:
* x:字符串x
* y:字符串y
* b:标志数组
* xlen:字符串x的长度
* ylen:字符串y的长度
*返回值:最长公共子序列的长度
*
*/
int Lcs_Length(string x, string y, int b[][Y+1],int xlen,int ylen)
{
int i = 0;
int j = 0;
//int c[X+1][Y+1];
for (i = 0; i<=xlen; i++)
{
c[i][0]=0;
}
for (i = 0; i <= ylen; i++ )
{
c[0][i]=0;
}
for (i = 1; i <= xlen; i++)
{
for (j = 1; j <= ylen; j++)
{
if (x[i - 1] == y[j - 1])
{
c[i][j] = c[i-1][j-1]+1;
b[i][j] = 1;
}
else
if (c[i-1][j] > c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 2;
}
else
if(c[i-1][j] <= c[i][j-1])
{
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
/*
cout << "计算最优值效果图如下所示:" << endl;
for(i = 1; i <= xlen; i++)
{
for(j = 1; j < ylen; j++)
{
cout << c[i][j] << " ";
}
cout << endl;
}
*/
return c[xlen][ylen];
}
void Display_Lcs(int i, int j, string x, int b[][Y+1],int current_Len)
{
if (i ==0 || j==0)
{
return;
}
if(b[i][j]== 1)
{
current_Len--;
result[current_Len]=x[i- 1];
Display_Lcs(i-1, j-1, x, b, current_Len);
}
else
{
if(b[i][j] == 2)
{
Display_Lcs(i-1, j, x, b, current_Len);
}
else
{
if(b[i][j]==3)
{
Display_Lcs(i, j-1, x, b, current_Len);
}
else
{
Display_Lcs(i-1,j,x,b, current_Len);
}
}
}
}
int main(int argc, char* argv[])
{
string x;
string y;
cin>>x>>y;
int xlen = x.length();
int ylen = y.length();
//int b[X + 1][Y + 1];
int lcs_max_len = Lcs_Length( x, y, b, xlen,ylen );
//cout << lcs_max_len << endl;
Display_Lcs( xlen, ylen, x, b, lcs_max_len );
//打印结果如下所示
for(int i = 0; i < lcs_max_len; i++)
{
cout << result[i];
}
cout << endl;
return 0;
}
算法复杂性:
• 时间复杂性
– 计算代价的时间
• (i, j)两层循环,i循环m步, j循环n步
• O(mn)
– 构造最优解的时间: O(m+n)
– 总时间复杂性为:O(mn)
• 空降复杂性
– 使用数组C和B
– 需要空间O(mn)
posted on 2017-01-25 10:23 KID_XiaoYuan 阅读(445) 评论(0) 编辑 收藏 举报




