「学习笔记」树链剖分
「学习笔记」树链剖分
点击查看目录
树链剖分
树链剖分就是把一棵树分成多个链,再维护每条链的信息。剖分的方法有很多种,如重链剖分,长链剖分。一般情况下,树链剖分指重链剖分。
算法
By OI-Wiki:
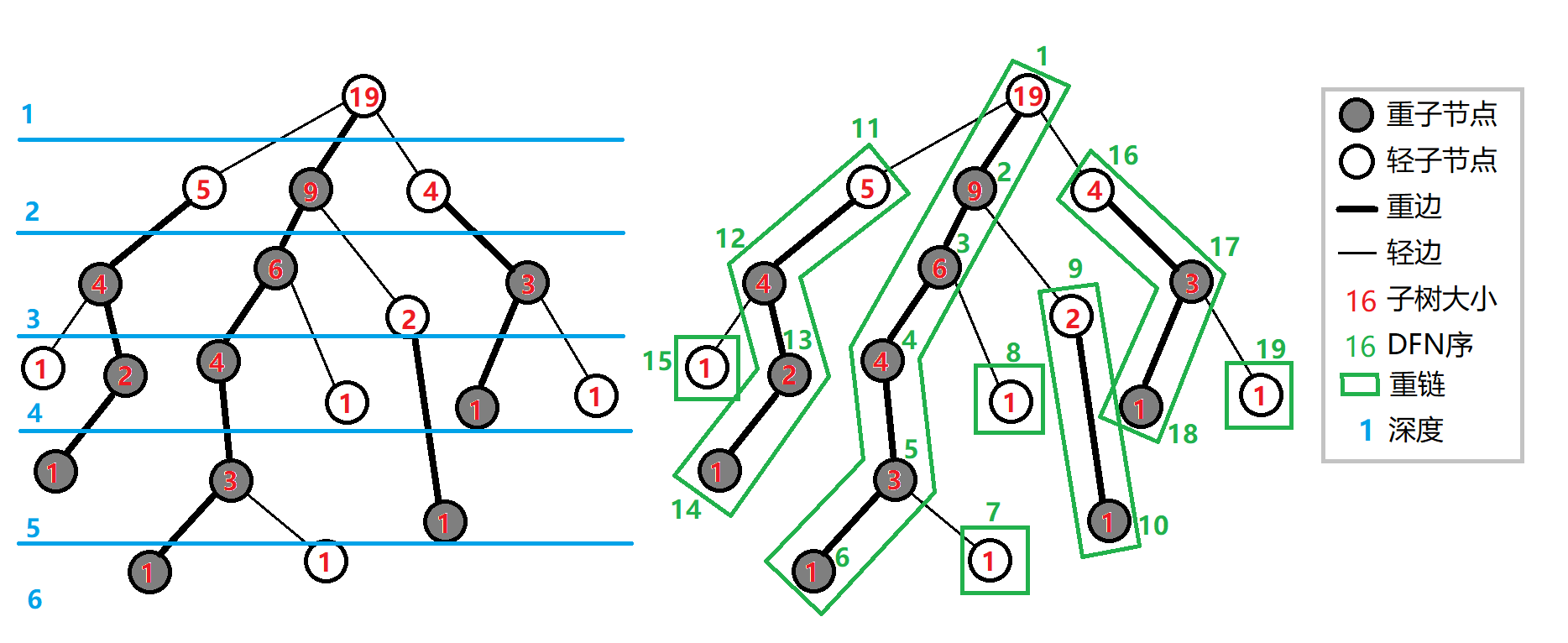
定义重子节点表示其子节点中子树最大的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。
定义轻子节点表示剩余的所有子结点。
从这个结点到重子节点的边为重边。
到其他轻子节点的边为轻边。
若干条首尾衔接的重边构成重链。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
如图:
为什么我要整段搬过来?因为除了上边那点东西本来就没什么可写的。
实现
首先我们要预处理出以下数组:
-
fa[u]:节点 \(u\) 的父亲。 -
dep[u]:节点 \(u\) 的深度。 -
sz[u]:以节点 \(u\) 为根的子树大小。 -
son[u]:节点 \(u\) 的重儿子。 -
top[u]:节点 \(u\) 所在链的链顶。 -
dfn[u]:节点 \(u\) 的 \(\operatorname{dfs}\) 序。 -
rk[u]:\(\operatorname{dfs}\) 序为 \(u\) 的节点。
这些东西并不难求,下面直接给出代码:
void Dfs1(ll u){
son[u]=-1,sz[u]=1;
far(v,tu[u]){
if(v==fa[u])continue;
dep[v]=dep[u]+1,fa[v]=u;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[v]>sz[son[u]])son[u]=v;//取重儿子
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);//优先遍历重儿子,因为这样可以保证一条链上的 dfs 序连续,方便数据结构处理!!!
far(v,tu[u])if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
return;
}
接下来问题是:如何更改和查询?
我们让输入的两个节点 \(u,v\) 不断往上跳,具体来说:
-
如果 \(u,v\) 在同一条链上,直接查询/修改两点的 \(\operatorname{dfs}\) 序之间的值。
-
如果 \(u,v\) 不在同一条链上,直接查询/修改 深度较深的节点 与 它所在链的链顶的节点 的 \(\operatorname{dfs}\) 序之间的值,并将其跳到它所在链的链顶的父亲。
例题
思路
单点修改直接在线段树上 \(dfs\) 序的位置改。
查询像上面说的边跳别查就行。
代码
点击查看代码
const ll N=3e4+10,inf=1ll<<40;
ll n,q,w[N];
vector<ll>tu[N];
ll fa[N],dep[N],sz[N],son[N];//dfs1
ll cnt=0,top[N],dfn[N],rk[N];//dfs2
class SegmentTree{
public:
class TREE{
public:
ll mx,va;
}tr[N<<2];
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mx(p) tr[p].mx
#define va(p) tr[p].va
#define l_s(p) ls(p),l,mid
#define r_s(p) rs(p),mid+1,r
inline void Pushup(ll p){
mx(p)=max(mx(ls(p)),mx(rs(p)));
va(p)=va(ls(p))+va(rs(p));
}
void Build(ll p,ll l,ll r){
if(l==r)mx(p)=va(p)=w[rk[l]];
else{
bdmd;
Build(l_s(p));
Build(r_s(p));
Pushup(p);
}
return;
}
void Update(ll p,ll l,ll r,ll x,ll val){
if(l>x||r<x)return;
if(l==r)mx(p)=va(p)=val;
else{
bdmd;
Update(l_s(p),x,val);
Update(r_s(p),x,val);
Pushup(p);
}
return;
}
ll QueryMax(ll p,ll l,ll r,ll le,ll ri){
if(r<le||ri<l)return -inf;
if(le<=l&&r<=ri)return mx(p);
bdmd;
return max(QueryMax(l_s(p),le,ri),QueryMax(r_s(p),le,ri));
}
ll QuerySum(ll p,ll l,ll r,ll le,ll ri){
if(r<le||ri<l)return 0;
if(le<=l&&r<=ri)return va(p);
bdmd;
return QuerySum(l_s(p),le,ri)+QuerySum(r_s(p),le,ri);
}
}tr;
class KillTree{
public:
void Dfs1(ll u){
son[u]=-1,sz[u]=1;
far(v,tu[u]){
if(v==fa[u])continue;
dep[v]=dep[u]+1,fa[v]=u;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[v]>sz[son[u]])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(v,tu[u])if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
return;
}
inline void Update(ll x,ll val){tr.Update(1,1,n,dfn[x],val);}
inline ll QueryMax(ll x,ll y){
ll num=-inf,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>=dep[ty])num=max(num,tr.QueryMax(1,1,n,dfn[tx],dfn[x])),x=fa[tx];
else num=max(num,tr.QueryMax(1,1,n,dfn[ty],dfn[y])),y=fa[ty];
tx=top[x],ty=top[y];
}
num=max(num,tr.QueryMax(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y])));
return num;
}
inline ll QuerySum(ll x,ll y){
ll num=0,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>=dep[ty])num+=tr.QuerySum(1,1,n,dfn[tx],dfn[x]),x=fa[tx];
else num+=tr.QuerySum(1,1,n,dfn[ty],dfn[y]),y=fa[ty];
tx=top[x],ty=top[y];
}
num+=tr.QuerySum(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y]));
return num;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline void In(){
n=rnt();
_for(i,1,n-1){
ll u=rnt(),v=rnt();
tu[u].push_back(v);
tu[v].push_back(u);
}
_for(i,1,n)w[i]=rnt();
kt.Dfs1(1),kt.Dfs2(1,1),tr.Build(1,1,n);
q=rnt();
ll c=0;
_for(i,1,q){
char s[10];
scanf("%s",s);
ll x=rnt(),y=rnt();
if(s[1]=='H')kt.Update(x,y);
else if(s[1]=='M')printf("%lld\n",kt.QueryMax(x,y));
else printf("%lld\n",kt.QuerySum(x,y));
}
return;
}
}
练习题
染色
思路
教训:板子没写熟别着急做难题。
我们用线段树维护颜色段数量:如果线段树上一个节点两个儿子首尾颜色相同,将颜色段数量加起来后还要去掉 \(1\)。
同一条链上颜色段数量的非常好维护,然后考虑如何合并不同链上的颜色段数量:
-
法一:记录上次跳完后的颜色,判断与现在的是否相等。
-
法二:当前节点跳到原链顶的父亲时,判断它与原链顶是否相等。
代码
点击查看代码
const ll N=2e5+10,inf=1ll<<40;
ll n,q,co[N],k[N];
vector<ll>tu[N];
ll fa[N],dep[N],sz[N],son[N];//dfs1
ll cnt=0,top[N],dfn[N],rk[N];//dfs2
class KillTree{
public:
class SegmentTree{
public:
class TREE{public:ll hd,tl,cnt,tag;}tr[N<<2];
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define hd(p) tr[p].hd
#define tl(p) tr[p].tl
#define cn(p) tr[p].cnt
#define ta(p) tr[p].tag
#define l_s(p) ls(p),l,mid
#define r_s(p) rs(p),mid+1,r
inline void Pushup(ll p){
hd(p)=hd(ls(p)),tl(p)=tl(rs(p));
cn(p)=cn(ls(p))+cn(rs(p));
if(tl(ls(p))==hd(rs(p)))--cn(p);
return;
}
inline void Tag(ll p,ll color){
cn(p)=1,ta(p)=color;
hd(p)=color,tl(p)=color;
return;
}
inline void Pushdown(ll p){
if(ta(p)==-1)return;
Tag(ls(p),ta(p));
Tag(rs(p),ta(p));
ta(p)=-1;
return;
}
void Build(ll p,ll l,ll r){
if(l==r)Tag(p,co[rk[l]]);
else{
bdmd;
Build(l_s(p));
Build(r_s(p));
Pushup(p);
}
ta(p)=-1;
return;
}
void Update(ll p,ll l,ll r,ll le,ll ri,ll color){
if(ri<l||r<le)return;
Pushdown(p);
if(le<=l&&r<=ri)Tag(p,color);
else{
bdmd;
Update(l_s(p),le,ri,color);
Update(r_s(p),le,ri,color);
Pushup(p);
}
return;
}
ll Query(ll p,ll l,ll r,ll le,ll ri){
if(ri<l||r<le)return 0;
Pushdown(p);
if(le<=l&&r<=ri)return cn(p);
else{
bdmd;
ll ans1=Query(l_s(p),le,ri);
ll ans2=Query(r_s(p),le,ri);
if(ans1>0&&ans2>0&&tl(ls(p))==hd(rs(p)))--ans1;
return ans1+ans2;
}
}
ll QueryP(ll p,ll l,ll r,ll x){
if(x<l||r<x)return 0;
Pushdown(p);
if(l==r)return hd(p);
else{
bdmd;
ll an=QueryP(l_s(p),x)+QueryP(r_s(p),x);
return an;
}
}
}tr;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(v,tu[u]){
if(v==fa[u])continue;
fa[v]=u,dep[v]=dep[u]+1;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[v]>sz[son[u]])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(v,tu[u])if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
return;
}
inline void Build(){fa[1]=1,Dfs1(1),Dfs2(1,1),tr.Build(1,1,n);}
inline void Update(ll x,ll y,ll color){
ll tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>=dep[ty])swap(x,y),swap(tx,ty);
tr.Update(1,1,n,dfn[ty],dfn[y],color),y=fa[ty];
tx=top[x],ty=top[y];
}
tr.Update(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y]),color);
}
inline ll Query(ll x,ll y){
ll num=0,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>=dep[ty])swap(x,y),swap(tx,ty);
num+=tr.Query(1,1,n,dfn[ty],dfn[y]),y=fa[ty];
if(y&&tr.QueryP(1,1,n,dfn[ty])==tr.QueryP(1,1,n,dfn[y]))--num;
tx=top[x],ty=top[y];
}
num+=tr.Query(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y]));
return num;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline char rch(){
char c=getchar();
while(c<'A'||c>'Z')c=getchar();
return c;
}
inline void In(){
n=rnt(),q=rnt();
_for(i,1,n)co[i]=rnt();
_for(i,1,n-1){
ll u=rnt(),v=rnt();
tu[u].push_back(v);
tu[v].push_back(u);
}
kt.Build();
_for(i,1,q){
char op=rch();
if(op=='C'){
ll a=rnt(),b=rnt(),op=rnt();
kt.Update(a,b,op);
}
else{
ll a=rnt(),b=rnt();
printf("%lld\n",kt.Query(a,b));
}
}
return;
}
}
QTREE
SPOJ 在机房上不去,垃圾洛谷 RemoteJudge 交不了 C++,只能用 Vjudge 凑合了。
思路
首先为了方便处理,我们化边权为点权,即把边权赋到深度较大的点上成为点权。
但是会有一个问题:查询到两点的 \(\text{LCA}\) 时,有可能多算一条边(即 \(\text{LCA}\) 与其父亲相连的那条边)。
那么我们暂时把它的点权设为 \(-\infty\),查询完再还原回来就可以了。
代码
点击查看代码
const ll N=2e4+10,inf=1ll<<40;
ll n,q,c[N],k[N];
class Edge{public:ll u,v,w;}e[N];
vector<pair<ll,ll> >tu[N];
ll fa[N],dep[N],sz[N],son[N];
ll cnt,top[N],dfn[N],rk[N];
class KillTree{
public:
class SegmentTree{
public:
ll mx[N<<4];
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define l_s(p) ls(p),l,mid
#define r_s(p) rs(p),mid+1,r
void Build(ll p,ll l,ll r){
if(l==r)mx[p]=c[rk[l]];
else{
bdmd;
Build(l_s(p)),Build(r_s(p));
mx[p]=max(mx[ls(p)],mx[rs(p)]);
}
return;
}
void Update(ll p,ll l,ll r,ll x,ll val){
if(r<x||x<l)return;
if(l==r)mx[p]=val;
else{
bdmd;
Update(l_s(p),x,val),Update(r_s(p),x,val);
mx[p]=max(mx[ls(p)],mx[rs(p)]);
}
return;
}
ll Query(ll p,ll l,ll r,ll le,ll ri){
if(r<le||ri<l)return -inf;
if(le<=l&&r<=ri)return mx[p];
else{
bdmd;
return max(Query(l_s(p),le,ri),Query(r_s(p),le,ri));
}
}
}tr;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(pr,tu[u]){
ll v=pr.first;
if(v==fa[u])continue;
c[v]=pr.second;
fa[v]=u,dep[v]=dep[u]+1;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(pr,tu[u]){
ll v=pr.first;
if(v!=fa[u]&&v!=son[u])
Dfs2(v,v);
}
return;
}
inline void Build(){Dfs1(1),Dfs2(1,1),tr.Build(1,1,n);}
inline void Update(ll x,ll y,ll z){
if(fa[y]==x)swap(x,y);
tr.Update(1,1,n,dfn[x],z);
return;
}
inline ll GetLCA(ll x,ll y){
ll tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>dep[ty])swap(x,y),swap(tx,ty);
y=fa[ty],ty=top[y];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
inline ll Query(ll x,ll y){
ll lca=GetLCA(x,y),la=tr.Query(1,1,n,dfn[lca],dfn[lca]);
tr.Update(1,1,n,dfn[lca],-inf);
ll num=-inf,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]>dep[ty])swap(x,y),swap(tx,ty);
num=max(num,tr.Query(1,1,n,dfn[ty],dfn[y])),y=fa[ty],ty=top[y];
}
num=max(num,tr.Query(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y])));
tr.Update(1,1,n,dfn[lca],la);
return num;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline char rch(){
char c=getchar();
while(c<'A'||c>'Z')c=getchar();
return c;
}
inline void Clear(){
_for(i,1,n)tu[i].clear();
memset(e,0,sizeof(e));
memset(fa,0,sizeof(fa));
memset(dep,0,sizeof(dep));
memset(sz,0,sizeof(sz));
memset(son,0,sizeof(son));
memset(top,0,sizeof(top));
memset(dfn,0,sizeof(dfn));
memset(rk,0,sizeof(rk));
memset(c,0,sizeof(c));
memset(k,0,sizeof(k));
memset(kt.tr.mx,0,sizeof(kt.tr.mx));
cnt=0;
}
inline void In(){
Clear();
n=rnt();
_for(i,1,n-1){
ll u=rnt(),v=rnt(),w=rnt();
e[i]=(Edge){u,v,w};
tu[u].push_back(make_pair(v,w));
tu[v].push_back(make_pair(u,w));
}
kt.Build();
while(1){
char op=rch();
if(op=='C'){
ll a=rnt(),b=rnt();
kt.Update(e[a].u,e[a].v,b);
}
else if(op=='Q'){
ll a=rnt(),b=rnt();
printf("%lld\n",kt.Query(a,b));
}
else return;
}
return;
}
}
[HAOI2015]树上操作
思路
操作 \(1,3\) 都是板子,很好求。考虑如何求操作 \(2\)。
一棵子树内的 DFS 序连续,那么我们更新一个节点 \(u\) 的子树时,直接在线段树上更改区间 \([dfn_u,dfn_u+size_u-1]\) 即可。
代码
点击查看代码
using namespace std;
const ll N=2e5+10,inf=1ll<<40;
ll n,q,c[N];
vector<ll>tu[N];
ll fa[N],dep[N],sz[N],son[N];
ll cnt,top[N],dfn[N],rk[N];
class KillTree{
public:
class SegmentTree{
public:
class TREE{public:ll val,sz,tag;}tr[N<<2];
#define va(p) tr[p].val
#define sz(p) tr[p].sz
#define ta(p) tr[p].tag
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define l_s(p) ls(p),l,mid
#define r_s(p) rs(p),mid+1,r
inline void Tag(ll p,ll tg){va(p)+=tg*sz(p),ta(p)+=tg;}
inline void PushUp(ll p){va(p)=va(ls(p))+va(rs(p));}
inline void PushDown(ll p){
if(!ta(p))return;
Tag(ls(p),ta(p));
Tag(rs(p),ta(p));
ta(p)=0;
return;
}
void Build(ll p,ll l,ll r){
sz(p)=r-l+1,ta(p)=0;
if(l==r)va(p)=c[rk[l]];
else{
bdmd;
Build(l_s(p));
Build(r_s(p));
PushUp(p);
}
return;
}
void Update(ll p,ll l,ll r,ll le,ll ri,ll val){
if(ri<l||r<le)return;
PushDown(p);
if(le<=l&&r<=ri)Tag(p,val);
else{
bdmd;
Update(l_s(p),le,ri,val);
Update(r_s(p),le,ri,val);
PushUp(p);
}
return;
}
ll Query(ll p,ll l,ll r,ll le,ll ri){
if(ri<l||r<le)return 0;
PushDown(p);
if(le<=l&&r<=ri)return va(p);
else{
bdmd;
ll ans1=Query(l_s(p),le,ri);
ll ans2=Query(r_s(p),le,ri);
return ans1+ans2;
}
}
}tr;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(v,tu[u]){
if(v==fa[u])continue;
fa[v]=u,dep[v]=dep[u]+1;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(v,tu[u])if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
return;
}
inline void Build(){Dfs1(1),Dfs2(1,1),tr.Build(1,1,n);}
inline void UpdateP(ll x,ll val){tr.Update(1,1,n,dfn[x],dfn[x],val);}
inline void UpdateR(ll x,ll val){tr.Update(1,1,n,dfn[x],dfn[x]+sz[x]-1,val);}
inline ll Query(ll x){
ll num=0,tx=top[x];
while(tx>=1){
num+=tr.Query(1,1,n,dfn[tx],dfn[x]);
x=fa[tx],tx=top[x];
}
return num;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline char rch(){
char c=getchar();
while(c<'A'||c>'Z')c=getchar();
return c;
}
inline void In(){
n=rnt(),q=rnt();
_for(i,1,n)c[i]=rnt();
_for(i,1,n-1){
ll u=rnt(),v=rnt();
tu[u].push_back(v);
tu[v].push_back(u);
}
kt.Build();
_for(i,1,q){
ll op=rnt(),a=rnt(),b=0;
if(op==1)b=rnt(),kt.UpdateP(a,b);
else if(op==2)b=rnt(),kt.UpdateR(a,b);
else printf("%lld\n",kt.Query(a));
}
return;
}
}
[NOIP2013 提高组] 货车运输
思路
给出的不是一棵树,但是我们可以发现查询只与路径上最小值相关,而不管距离,所以我们只留下一些有用的边即可,即求出一棵最小生成树。
剩下的就是板子了。
代码
点击查看代码
const ll N=1e5+10,inf=1ll<<40;
ll n,m,q,c[N],k[N];
vector<pair<ll,ll> >tu[N];
ll fa[N],dep[N],sz[N],son[N];
ll cnt,top[N],dfn[N],rk[N];
class BCJ{
public:
ll f[N];
inline void Pre(){_for(i,1,n)f[i]=i;}
ll Find(ll x){return (f[x]==x)?x:(f[x]=Find(f[x]));}
inline void Merge(ll x,ll y){f[y]=x;}
}bcj;
namespace Kru{
class Edge{
public:
ll u,v,w;
inline bool operator<(const Edge &d)const{return w>d.w;}
}e[N];
inline void Add(ll i,ll u,ll v,ll w){e[i].u=u,e[i].v=v,e[i].w=w;}
inline void Solve(){
sort(e+1,e+m+1);
ll k=0;
bcj.Pre();
_for(i,1,m){
ll fu=bcj.Find(e[i].u),fv=bcj.Find(e[i].v);
if(fu!=fv){
tu[e[i].u].push_back(make_pair(e[i].v,e[i].w));
tu[e[i].v].push_back(make_pair(e[i].u,e[i].w));
bcj.Merge(fu,fv);
++k;
}
if(k==n-1)break;
}
return;
}
}
class KillTree{
public:
class SegmentTree{
public:
class TREE{public:ll mn;}tr[N<<2];
#define mn(p) tr[p].mn
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define l_s(p) (p<<1),l,mid
#define r_s(p) (p<<1|1),mid+1,r
void Build(ll p,ll l,ll r){
if(l==r)mn(p)=c[rk[l]]?c[rk[l]]:inf;
else{
bdmd;
Build(l_s(p)),Build(r_s(p));
mn(p)=min(mn(ls(p)),mn(rs(p)));
}
return;
}
ll Query(ll p,ll l,ll r,ll le,ll ri){
if(ri<l||r<le)return inf;
if(le<=l&&r<=ri)return mn(p);
else{
bdmd;
return min(Query(l_s(p),le,ri),Query(r_s(p),le,ri));
}
}
}tr;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(pr,tu[u]){
ll v=pr.first,w=pr.second;
if(v==fa[u])continue;
c[v]=w,fa[v]=u,dep[v]=dep[u]+1;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(pr,tu[u]){
ll v=pr.first;
if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
}
return;
}
inline void Build(){Dfs1(1),Dfs2(1,1),tr.Build(1,1,n);}
inline ll Query(ll x,ll y){
if(bcj.Find(x)!=bcj.Find(y))return -1;
ll num=inf,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]<dep[ty])swap(x,y),swap(tx,ty);
num=min(num,tr.Query(1,1,n,dfn[tx],dfn[x]));
x=fa[tx],tx=top[x];
}
if(x!=y)num=min(num,tr.Query(1,1,n,min(dfn[x],dfn[y])+1,max(dfn[x],dfn[y])));
return num;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline char rch(){
char c=getchar();
while(c<'A'||c>'Z')c=getchar();
return c;
}
inline void In(){
n=rnt(),m=rnt();
_for(i,1,m){
ll u=rnt(),v=rnt(),w=rnt();
Kru::Add(i,u,v,w);
}
Kru::Solve();
kt.Build();
q=rnt();
_for(i,1,q){
ll x=rnt(),y=rnt();
printf("%lld\n",kt.Query(x,y));
}
return;
}
}
[NOIP2015 提高组] 运输计划
思路
毒瘤好题。
首先老套路化边权为点权。
考虑去掉哪一条边才会产生贡献:显然是耗时最久的飞船经过的某条边。
那么我们维护一个数组 \(q\),\(q_i\) 表示不经过节点 \(i\) 的飞船中的最长时间,这样只要枚举耗时最久的飞船经过的所有边就可以了。
那么如何维护一个数组 \(q\) 呢?我们可以发现两点之间的路径会被树链截成若干个不相交的 \(\text{dfs}\) 序区间,那么我们对这些区间排个序,将相邻区间之间形成的区间打上当前答案的标记即可。
然后说一下我踩过的坑:
-
读错题,飞船应是同时出发的。(\(0\text{pts}\longrightarrow15\text{pts}\))
-
#define ls(p) (p<<2)(\(15\text{pts}\longrightarrow55\text{pts}\)) -
新来的标记把原标记覆盖了,但可能原标记才是有用的。(\(55\text{pts}\longrightarrow95\text{pts}\))
-
答案可能为 \(0\),但由于 \(x=y\) ,\(\text{ans}\) 压根就没更新,还是 \(\infty\),可以通过 \(\bmod{\infty}\) 解决。(\(95\text{pts}\longrightarrow100\text{pts}\))
代码
点击查看代码
const ll N=3e6+10,inf=1ll<<40;
ll n,m,q,c[N],ans=inf,lgst,lx,ly;
vector<pair<ll,ll> >tu[N];
ll fa[N],dep[N],sz[N],son[N];
ll cnt,top[N],dfn[N],rk[N];
class KillTree{
public:
class TreeArray{
public:
ll b[N];
inline void Update(ll x,ll y){while(x&&x<=n)b[x]+=y,x+=(x&-x);}
inline ll Query(ll x){ll sum=0;while(x)sum+=b[x],x-=(x&-x);return sum;}
inline void Build(){_for(i,1,n)Update(i,c[rk[i]]);}
}tra;
class SegmentTree{
public:
class Tree{public:ll mx,tag,sz;}tr[N<<2];
#define sz(p) tr[p].sz
#define mx(p) tr[p].mx
#define ta(p) tr[p].tag
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define l_s(p) (p<<1),l,mid
#define r_s(p) (p<<1|1),mid+1,r
inline void Tag(ll p,ll tg){if(tg>ta(p))ta(p)=tg,mx(p)=max(mx(p),tg);}
inline void PushUp(ll p){mx(p)=max(mx(ls(p)),mx(rs(p)));}
inline void PushDown(ll p){if(ta(p))Tag(ls(p),ta(p)),Tag(rs(p),ta(p)),ta(p)=0;}
void Build(ll p,ll l,ll r){
ta(p)=0,sz(p)=r-l+1;
if(l==r)mx(p)=0;
else{
bdmd;
Build(l_s(p)),Build(r_s(p));
PushUp(p);
}
return;
}
void Update(ll p,ll l,ll r,ll le,ll ri,ll val){
if(ri<l||r<le)return;
PushDown(p);
if(le<=l&&r<=ri)Tag(p,val);
else{
bdmd;
Update(l_s(p),le,ri,val);
Update(r_s(p),le,ri,val);
PushUp(p);
}
}
ll Query(ll p,ll l,ll r,ll x){
if(x<l||r<x)return 0;
PushDown(p);
if(l==r)return mx(p);
else{
bdmd;
return max(Query(l_s(p),x),Query(r_s(p),x));
}
}
}set;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(pr,tu[u]){
ll v=pr.first,w=pr.second;
if(v==fa[u])continue;
fa[v]=u,dep[v]=dep[u]+1,c[v]=w;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(pr,tu[u]){
ll v=pr.first;
if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
}
return;
}
inline void Build(){Dfs1(1),Dfs2(1,1),tra.Build(),set.Build(1,1,n);}
inline ll Query(ll x,ll y){
ll num=0,tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]<dep[ty])swap(x,y),swap(tx,ty);
num+=tra.Query(dfn[x])-tra.Query(dfn[tx]-1);
x=fa[tx],tx=top[x];
}
num+=tra.Query(max(dfn[x],dfn[y]))-tra.Query(min(dfn[x],dfn[y]));
return num;
}
inline void Add(ll x,ll y){
ll tx=top[x],ty=top[y],num=Query(x,y);
if(num>lgst)lgst=num,lx=x,ly=y;
vector<pair<ll,ll> >e;
while(tx!=ty){
if(dep[tx]<dep[ty])swap(x,y),swap(tx,ty);
e.push_back(make_pair(dfn[tx],dfn[x]));
x=fa[tx],tx=top[x];
}
if(dep[x]<dep[y])swap(x,y);
e.push_back(make_pair(dfn[y]+1,dfn[x]));
sort(e.begin(),e.end());
if(!e.empty()){
ll sz=e.size()-1;
if(e[0].first!=1)set.Update(1,1,n,1,e[0].first-1,num);
if(e[sz].second!=n)set.Update(1,1,n,e[sz].second+1,n,num);
_for(i,1,sz){
if(e[i-1].second+1==e[i].first)continue;
set.Update(1,1,n,e[i-1].second+1,e[i].first-1,num);
}
}
return;
}
inline ll Solve(){
while(lx!=ly){
if(dep[lx]<dep[ly])swap(lx,ly);
ans=min(ans,max(lgst-c[lx],set.Query(1,1,n,dfn[lx])));
lx=fa[lx];
}
return ans;
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline char rch(){
char c=getchar();
while(c<'A'||c>'Z')c=getchar();
return c;
}
inline void In(){
n=rnt(),m=rnt();
_for(i,1,n-1){
ll u=rnt(),v=rnt(),w=rnt();
tu[u].push_back(make_pair(v,w));
tu[v].push_back(make_pair(u,w));
}
kt.Build();
_for(i,1,m){
ll x=rnt(),y=rnt();
if(x!=y)kt.Add(x,y);
}
printf("%lld\n",kt.Solve()%inf);
return;
}
}
遥远的国度
思路
只要想清楚了就很简单。
开个变量 \(\text{root}\) 记录当前根,修改是常规树剖。
然后考虑如何查询,我们设当前查询节点 \(u\),然后分情况讨论:
- \(u\) 就是 \(\text{root}\):直接查询整棵树。
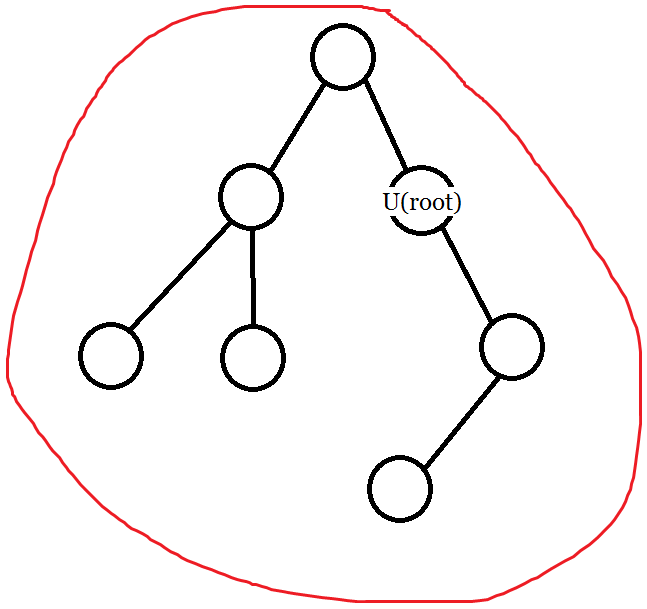
- \(\text{root}\) 是 \(u\) 祖先:直接查询以 \(u\) 为根的子树。
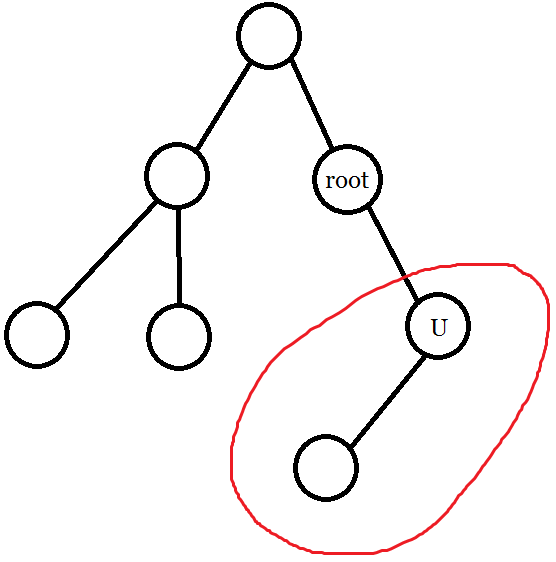
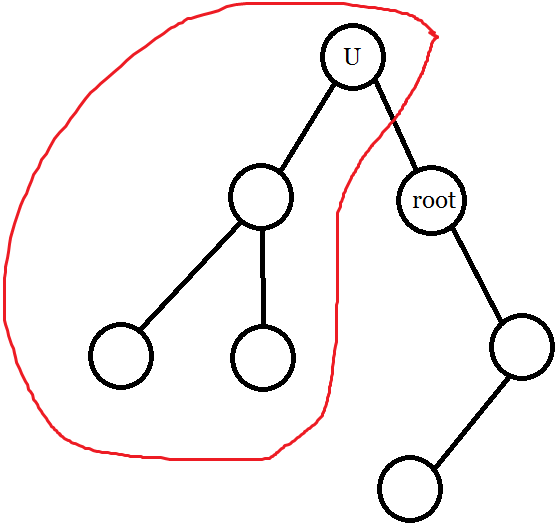
- \(u\) 是 \(\text{root}\) 祖先:直接把以 \(u\) 为根的子树刨去。即设以 \(u\) 为根的子树对应的区间为 \([l,r]\),则查询区间 \([1,l-1]\) 和 \([r+1,n]\) 的最小值。
代码
点击查看代码
const ll N=2e5+10,inf=1ll<<40;
ll n,m,root,val[N],ans;
vector<ll>tu[N];
ll fa[N],dep[N],sz[N],son[N];
ll cnt,top[N],dfn[N],rk[N];
class KillTree{
public:
class SegmentTree{
public:
class{public:ll va,ta;}tr[N<<2];
#define va(p) tr[p].va
#define ta(p) tr[p].ta
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define l_s(p) (p<<1),l,mid
#define r_s(p) (p<<1|1),mid+1,r
inline void Tag(ll p,ll tg){va(p)=ta(p)=tg;return;}
inline void PushUp(ll p){va(p)=min(va(ls(p)),va(rs(p)));}
inline void PushDown(ll p){
if(ta(p)==-1)return;
Tag(ls(p),ta(p));
Tag(rs(p),ta(p));
ta(p)=-1;
return;
}
void Build(ll p,ll l,ll r){
ta(p)=-1;
if(l==r)va(p)=val[rk[l]];
else{
bdmd;
Build(l_s(p)),Build(r_s(p));
PushUp(p);
}
return;
}
void Update(ll p,ll l,ll r,ll le,ll ri,ll val){
if(ri<l||r<le)return;
PushDown(p);
if(le<=l&&r<=ri)Tag(p,val);
else{
bdmd;
Update(l_s(p),le,ri,val);
Update(r_s(p),le,ri,val);
PushUp(p);
}
return;
}
ll Query(ll p,ll l,ll r,ll le,ll ri){
if(ri<l||r<le)return inf;
PushDown(p);
if(le<=l&&r<=ri)return va(p);
else{
bdmd;
return min(Query(l_s(p),le,ri),Query(r_s(p),le,ri));
}
}
}tr;
void Dfs1(ll u){
sz[u]=1,son[u]=-1;
far(v,tu[u]){
if(v==fa[u])continue;
fa[v]=u,dep[v]=dep[u]+1;
Dfs1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v])son[u]=v;
}
return;
}
void Dfs2(ll u,ll t){
top[u]=t;
dfn[u]=++cnt;
rk[cnt]=u;
if(son[u]==-1)return;
Dfs2(son[u],t);
far(v,tu[u])if(v!=fa[u]&&v!=son[u])Dfs2(v,v);
return;
}
inline void Build(){Dfs1(1),Dfs2(1,1),tr.Build(1,1,n);}
inline void Update(ll x,ll y,ll z){
ll tx=top[x],ty=top[y];
while(tx!=ty){
if(dep[tx]<dep[ty])swap(x,y),swap(tx,ty);
tr.Update(1,1,n,dfn[tx],dfn[x],z);
x=fa[tx],tx=top[x];
}
if(dep[x]<dep[y])swap(x,y);
tr.Update(1,1,n,dfn[y],dfn[x],z);
}
inline ll Query(ll x,ll y){
ll q=x,tx=top[x],ty=top[y],s=x;
while(tx!=ty){
if(dep[tx]<dep[ty])s=y,y=fa[ty],ty=top[y];
else x=fa[tx],tx=top[x];
}
if(x!=y)s=son[x];
if(dep[x]>dep[y])swap(x,y);
if(q==root)return tr.Query(1,1,n,1,n);
else if(x!=q)return tr.Query(1,1,n,dfn[q],dfn[q]+sz[q]-1);
else return min(tr.Query(1,1,n,1,dfn[s]-1),tr.Query(1,1,n,dfn[s]+sz[s],n));
}
}kt;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline void In(){
n=rnt(),m=rnt(),root=1;
_for(i,1,n-1){
ll u=rnt(),v=rnt();
tu[u].push_back(v);
tu[v].push_back(u);
}
_for(i,1,n)val[i]=rnt();
root=rnt();
kt.Build();
_for(i,1,m){
ll op=rnt();
if(op==1)root=rnt();
else if(op==2){
ll x=rnt(),y=rnt(),z=rnt();
kt.Update(x,y,z);
}
else{
ll x=rnt();
printf("%lld\n",kt.Query(x,root));
}
}
return;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号