「杂题乱写」AGC 001
「杂题乱写」AGC 001
点击查看目录
A | BBQ Easy
排序奇数项求和,贪心正确性显然。
B | Mysterious Light
发现可以分割成若干个等边三角形,考虑计算等边三角形的边长之和。
发现边长就是 \(n - x\) 与 \(x\) 不断更相减损,其和为 \(n - \gcd(n, x)\)。
那么答案就是 \(3(n - \gcd(n, x))\)。
C | Shorten Diameter
枚举直径中心,判断多少个点与这个中心距离小于等于 \(\left\lfloor\frac{k}{2}\right\rfloor\) 即可得知需要扔几个点。\(k\) 为奇数中心是条边,是偶数中心是个点。
D | Arrays and Palindrome
有趣的构造题。
不难发现把每个数看成一个点,那么要求一个子串为回文可以转化为一堆点连边,两个点联通说明这两个数相等,如下图:
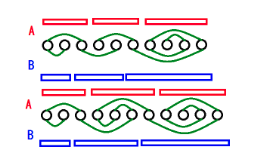
一个合理的构造是直接错排一位,如上图。
但是注意一个长度为奇数的回文的中心不会连边,如果这样的回文数量大于 \(2\),用 \(b\) 数组是无法解决的,否则需要特殊处理一下。
点击查看代码
const ll N = 1e5 + 10;
namespace SOLVE {
ll n, m, a[N], c1, ans, b[N];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline ll cmp (ll x, ll y) { return (x & 1) > (y & 1); }
inline void In () {
n = rnt (), m = rnt ();
_for (i, 1, m) a[i] = rnt (), c1 += a[i] & 1;
return;
}
inline void Solve () {
if (m == 1) {
ans = 2, b[1] = 1, b[2] = a[1] - 1;
return;
}
if (c1 > 2) { ans = -1; return; }
std::sort (a + 1, a + m + 1, cmp);
_for (i, 3, m) std::swap (a[i], a[i - 1]);
b[++ans] = a[1] + 1;
_for (i, 2, m - 1) b[++ans] = a[i];
b[++ans] = a[m] - 1;
return;
}
inline void Out () {
if (ans == -1) { puts ("Impossible"); return; }
if (!b[ans]) --ans;
_for (i, 1, m) printf ("%lld ", a[i]);
printf ("\n%lld\n", ans);
_for (i, 1, ans) printf ("%lld ", b[i]);
puts ("");
return;
}
}
E | BBQ Hard
这个 trick 我是真想不到。jjdw 说这个 trick 是类似「来自学长的馈赠 1」的,看了一下确实,越学越倒退是吧。
一个比较经典的东西是 \(\dbinom{x + y}{x}\) 可表示从 \((0, 0)\) 出发只能向右或向上走走到 \((x, y)\) 的方案数。
那么 \(\dbinom{a_i + b_i + a_j + b_j}{a_i + a_j}\) 的组合意义就是从 \((-a_i, -b_i)\) 出发只能向右或向上走走到 \((a_j, b_j)\) 的方案数。
那么设 \(f_{x, y}\) 表示共有多少种方案可以走到 \((x, y)\),初始所有 \(f_{-a_i, -b_i}\) 为 \(1\)。转移方程:\(f_{i, j} \leftarrow f_{i, j} + f_{i - 1, j} + f_{i, j - 1}\)。
注意到会把从 \((-a_i, -b_i)\) 走到 \((a_i, b_i)\) 给算上,这一部分是多余的。同时还要求 \(i < j\),因此答案要除二。那么最后统计答案为 \(\dfrac{1}{2}\sum_{i = 1}^{n}(f_{a_i, b_i} - \dbinom{2a_i + 2b_i}{2a_i})\)。
点击查看代码
const ll N = 2e5 + 10, M = 4e3 + 10, P = 1e9 + 7;
namespace SOLVE {
ll n, a[N], b[N], f[M][M], ans;
ll fac[M << 1], inv[M << 1];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline ll FastPow (ll a, ll b) {
ll ans = 1;
while (b) {
if (b & 1) ans = ans * a % P;
a = a * a % P, b >>= 1;
}
return ans;
}
inline ll C (ll x, ll y) { return fac[x] * inv[y] % P * inv[x - y] % P;}
inline void Pre () {
fac[0] = 1;
_for (i, 1, 8000) fac[i] = fac[i - 1] * i % P;
inv[8000] = FastPow (fac[8000], P - 2);
for_ (i, 7999, 0) inv[i] = inv[i + 1] * (i + 1) % P;
return;
}
inline void In () {
n = rnt ();
_for (i, 1, n) a[i] = rnt (), b[i] = rnt ();
return;
}
inline void Solve () {
Pre ();
_for (i, 1, n) ++f[2001 - a[i]][2001 - b[i]];
_for (i, 1, 4001) _for (j, 1, 4001) f[i][j] = (f[i][j] + f[i - 1][j] + f[i][j - 1]) % P;
_for (i, 1, n) {
ll qwq = f[a[i] + 2001][b[i] + 2001];
ll awa = C (2 * (a[i] + b[i]), 2 * a[i]);
ans = (ans + qwq - awa + P) % P;
}
return;
}
inline void Out () {
printf ("%lld\n", ans * FastPow (2, P - 2) % P);
return;
}
}
F | Wide Swap
首先转化,定义一个序列 \(Q\) 使得 \(Q_{p_i} = i\)。然后发现交换条件变成了相邻两个数绝对值大于等于 \(k\) 时可以交换。
那么考虑使用一些特殊方法排序,注意到对于一个数对 \((Q_i, Q_j)(i < j)\),当 \(\min_{k = i}^{j - 1}Q_k \ge Q_j + k\) 时两者可以交换过来且对答案作正贡献。
那么考虑归并排序,维护前一半的后缀最小值。
点击查看代码
const ll N = 5e5 + 10;
namespace SOLVE {
ll n, k, a[N], b[N], mn[N], ans[N];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline void Merge (ll l, ll r) {
if (l == r) return;
bdmd; Merge (l, mid), Merge (mid + 1, r);
ll po = l - 1, pl = l, pr = mid + 1;
mn[mid] = a[mid];
for_ (i, mid - 1, l) mn[i] = std::min (mn[i + 1], a[i]);
while (pl <= mid && pr <= r) {
if (mn[pl] >= a[pr] + k) b[++po] = a[pr++];
else b[++po] = a[pl++];
}
while (pl <= mid) b[++po] = a[pl++];
while (pr <= r) b[++po] = a[pr++];
_for (i, l, r) a[i] = b[i];
return;
}
inline void In () {
n = rnt (), k = rnt ();
_for (i, 1, n) a[rnt ()] = i;
return;
}
inline void Solve () {
Merge (1, n);
_for (i, 1, n) ans[a[i]] = i;
return;
}
inline void Out () {
_for (i, 1, n) printf ("%lld\n", ans[i]);
return;
}
}
整了个好玩的:
这是官方题解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号