「闲话随笔」双极定向问题
做多校的小朋友们你们好呀(?)
一些定义:
- 「耳(Ear)」:若对于 \(G = (V, E)\) 的子图 \(G' = (V', E')\) 存在 \(x_1, x_2, \cdots, x_k\),满足 \(x_1, x_k\in V', x_2, \cdots, x_{k - 1}\notin V'\) 且 \(\forall i > 1, (x_{i - 1}, x_i)\in E\),则称顶点序列 \(x\) 是 \(G'\) 的耳 . 特别的,当 \(x_1\neq x_k\) 时,称这个耳为开耳 .
- 「耳分解(Ear Decomposition)」:若图 \(G\) 的一个子图序列 \(G_0, G_1, \cdots, G_k\) 满足 \(G_0\) 仅存在一个点或两个点及两点之间的一条边,\(G_k = G, \forall i > 0, G_{i - 1}\subsetneqq G_{i}\),且 \(G_{i}\setminus G_{i - 1}\) 是 \(G_{i - 1}\) 的一个耳,则称该子图序列为 \(G\) 的一个耳分解 . 特别的,若所有 \(G_{i}\setminus G_{i - 1}\) 都是 \(G_{i - 1}\) 的开耳,则称该耳分解为开耳分解 .
有结论:
- \(G\) 是边双 \(\iff\) \(G\) 存在耳分解 .
- \(G\) 是点双 \(\iff\) \(G\) 存在开耳分解 .
给定一张无向连通图 \(G\) 和点 \(S, T\),要求对每条边定向,使得 \(G\) 成为一张 DAG,且有且仅有 \(S\) 入度为零,有且仅有 \(T\) 出度为零 .
假设加入 \((S, T)\) 后 \(G\) 是点双,那么可以通过开耳分解构造,即初始对 \(S\rightarrow T\) 定向,之后每次将分解出的开耳 \(x\) 的相邻边按 \((x_1, x_k)\) 的方向定向,可以保证该耳一定是从 \(S\) 指向 \(T\) 的 . 如果初始没有边 \((S, T)\) 也没关系,可以假装有一下,因为 \((S, T)\) 的作用是插入第一个耳 \(S\rightsquigarrow T\),没有这条边也可以钦定插入这个耳 . 注意如果 \(G\) 仅满足边双那么分解出来的耳存在非开耳,会构造出环,导致结果不是 DAG .
那么接下来需要解决的是对一张图进行耳分解 . 考虑以 \(S\) 为根建立 DFS 树,维护一个队列,每个元素是一个二元组表示将点 \(u\) 到其第一个被定向过的祖先经过的路径上所有边如何定向 . 每次取出队首按要求定向时,将经过的所有耳加入队列 . 形式化的,如果当前正在对 \((u, v)\) 定向,存在一条返祖边 \((x, u)\),使得 \(x\) 在 \(v\) 子树内,那么应按下图绿箭头对耳 \(u\rightsquigarrow v\) 定向,\(u\rightarrow x\) 可以直接在遍历到时处理,\(x\rightsquigarrow v\) 加入队列 .
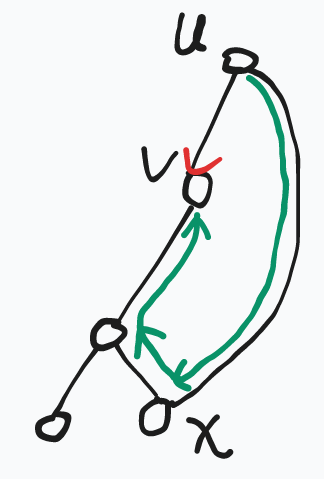
任何时刻被定向的边都是一个包含根的连通块,加入每个耳都是在对这个连通块向下延伸,由于原图加入 \((S, T)\) 后是点双,最终一定能保证每条树边和返祖边都被耳覆盖 . 定向的正确性则显然 .
由于每条边都被覆盖恰好一次,时间复杂度是 \(O(n + m)\) .
给定一个 \(n_1 + n_2\) 个点 \(m\) 条边的点双,要求将其分成两个大小分别为 \(n_1, n_2\) 的连通导出子图 .
\(1\le n_1, n_2\le 2000, 1\le m\le 5000\) .
其实官解有平方做法,不过我们暂且不理 .
经典结论:对于任意 DAG \(G\) 的一个任意拓扑序 \(p\),\(p\) 的任意前缀和任意后缀均连通 .
由于原图是点双,可以考虑随便双极定向一下然后拓扑排序拉下来前 \(n_1\) 个数 . 复杂度是线性的,比官解优秀 .


