浅谈Link-Cut Tree(LCT)

0XFF 前言&概念

Link-Cut Tree 是一种用来维护动态森林连通性的数据结构，适用于动态树问题。它采用类似树链剖分的轻重边路径剖分，把树边分为实边和虚边，并用 Splay 来维护每一条实路径。Link-Cut Tree 的基本操作复杂度为均摊O(logn），但常数因子较大，一般效率会低于树链剖分。但是却可以解决树链剖分解决不了的问题(或者优化码量) -----Menci dalao

动态树LCT(link cut tree)是一个可以动态维护森林上各种信息的东西(删除查找合并啥的都有吧)，原来的森林我们称为原森林，里面有实边和虚边，为啥有这两种边呢，首先LCT是用很多个splay维护这个森林的信息，那么因为splay本来就是个二叉树，所以我们要将原森林”剖分”成很多个二叉树并且用splay来维护它，用实边连接起来的一棵树就是原森林中的一棵树，我们称它为原树。

这个Splay会有些特殊，它的关键字是节点在树里面的深度。

这棵原树我们也不是直接用splay维护，而是按每个点在原树中的深度为优先级，将每个点以优先级的中序遍历丢到splay上。我们一般将原树所对应的splay称为辅助树，原森林就对应一个辅助树森林。
-----quhengyi11 dalao

请务必先将上文读清楚，再继续下面的阅读。

Splay是辅助树，阅读时不要将主的和辅的搞混了。

显然原树中同一个深度的点是不可能在一个splay里的，因此每个splay里面就是维护了原树中的一条链

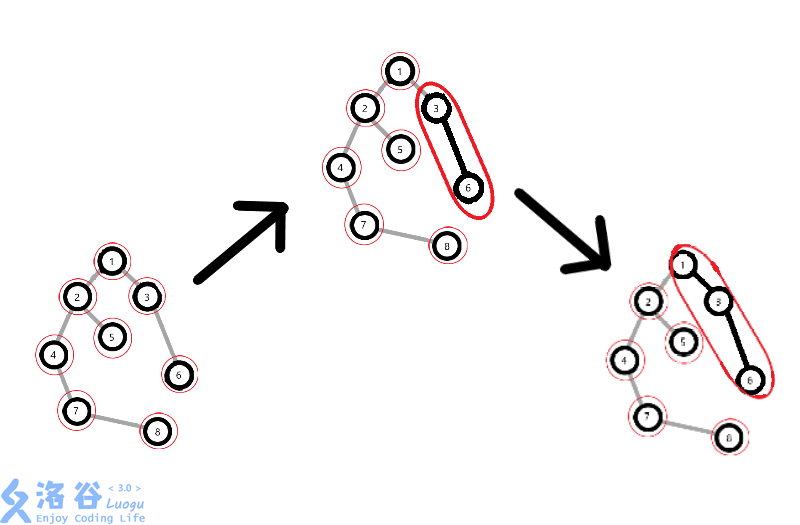
Link-Cut Tree 准确的说是一个 Splay 森林。每棵 Splay 都用"虚边"链接(下图灰边表示虚边)，每棵 Splay 中的结点都用"实边"链接起来(下图用黑色表示实边)。假如我们现在有一个栗子：(用红色圈圈圈在一起的结点是一个 Splay 中的结点)

LCT

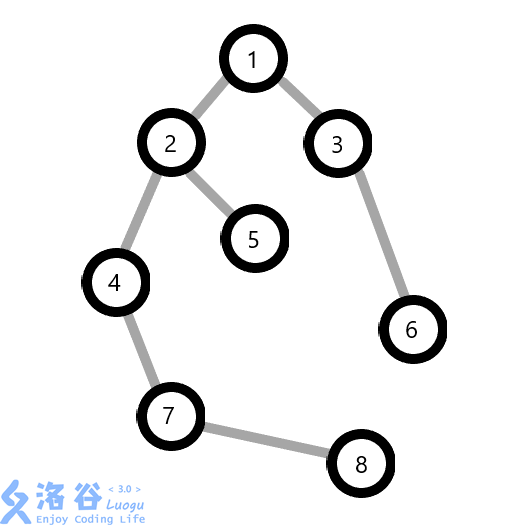
那么现在每个结点都是一颗 Splay。

就像这样：

LCT

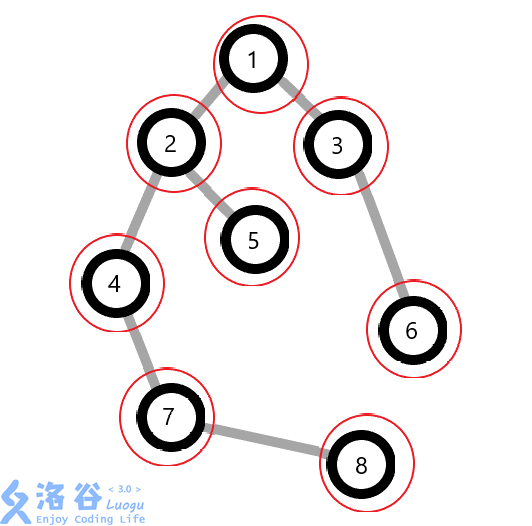
如果我们将1,2连接起来的话。

那么1,2就是同一个 Splay 中的节点了。

那么现在的情况就是这样：

LCT

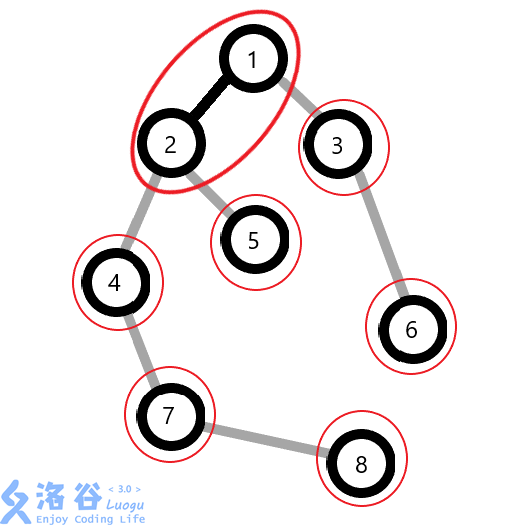
相信你一定对此有些了解了吧。

0X01 一些基本的定义

f[x]:结点x的爸爸(father)

v[x]:结点x的权值(value)

s[x]:结点x及它的子树的权值和(sum)

r[x]:结点x的翻转情况(rev)

ch[x][0/1]:结点x的左/右儿子

0X02 一些操作

Link-Cut Tree 支持以下几种基本操作：

Access(x)：将x到根节点的路径上全部变成实边，并弃掉自己所有的儿子(变成虚边：认父不认子)(每一个父结点对于自己的每个子结点只有一条实边)

findroot(x):找出x所在的原树的根结点(实际上就是上图的一号点)

makeroot(x):这个操作的意思是将x点变为原树的根节点

split(x,y):将x,y搞在一个 Splay 中，以方便操作。

link(x,y):将x和y所在原树合并起来(链接)

cut(x,y):将x和y所在原树拆开(切断)

Access(x):

这是最基础的操作，意思是将点x到原树中根结点root之间的链丢到一个辅助树splay里面

比方说，现在森林的状态是这样的：

LCT

我们的 x 现在等于6。执行 Access(6) 。

那么就会将{1-3，3-6}变成实边，1-2变成虚边，假设6有一儿子n，之间用实边连着，那么这条边也将变成虚边。

每次将\(x\)点 splay 到当前所在辅助树的根节点，将它的右儿子更新为上一个\(x\)，然后令\(x\)跳到它的父节点，特别的，第一个\(x\)的右儿子设为0(NULL)。

Q：为什么是右儿子而不是左儿子呢？

A：因为f[x]的深度小于x，而在Splay里面f[x]是x的爸爸，所以x在Splay中是f[x]的右儿子。

所以就变成了这样：

LCT

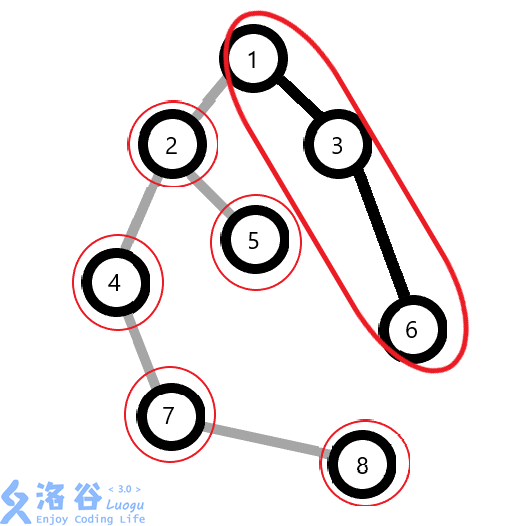
我们将\(x\)旋转到辅助树的根节点，也就是将当前原树这条链上深度小于\(x\)(在\(x\)上面的点)丢到了\(x\)的左子树上，将\(x\)的右子树设为上一个\(x\)点相当于将\(x\)原来的右子树丢到了新的 splay 里面(而它们之间用虚边相连)，并且将上一段链连接起来。

现在就可以了。这棵新 Splay 中只有这条链上的结点，没有其他任何的结点。如果我们指定要这三个结点同时进行操作，可以直接下传懒标记到这三个结点组成的 Splay 的根结点哦!到后面Splay的时候就可以直接下传跟新结点信息了。

总体过程：

LCT

虚边：儿子认父，父不认子

实边：儿子认父，父也认子

用FlashHu大佬的话来说，就是四步：

1.转到根。

2.换儿子。

3.更新信息。

4.当前操作点切换为轻边所指的父亲，转1。

代码实现：

inline void Access(int x){
      for(register int y=0;x;y=x,x=f[x]){
            Splay(x);//转到所在Splay的根节点
            ch[x][1]=y;//认儿子了
            pushup(x);//儿子有变化，更新
      }
}

findroot(x):
首先要明白：
根节点是的深度最小的

我们可以通过x向上找，用 Access 操作可以将x和x的根结点搞到一个 Splay 里。

又因为有BST的性质：x的左子树所有结点的权值 < x < x右子树所有结点的权值。

而我们又知道，在执行完 Access 操作后，这课 Splay 里面的结点权值最大的(深度最大的)就是x。

于是我们可以将x Splay 到这棵 Splay 的根结点，那么现在最左边的节点便是这课树的根结点了。

代码实现：

inline int findroot(int x){
      Access(x);//Access将x和根结点搞到同一个Splay中
      Splay(x);//转到Splay的根结点
      while(ch[x][0])pushdown(x),x=ch[x][0];//不断的找左儿子&更新节点信息
      return x;//最左边的就是根结点了。
}

makeroot(x):

将x到根结点的路径上的点全部翻转(即x变成了根节点)

具体操作是我们先将x点与原树中的根打通一条链，那么现在它们就在同一棵辅助树里面了，我们发现x一定是在它所在的辅助树的中序遍历的最后一个的(因为它是这条链上最深的点)，我们把x点 splay 到辅助树的根上，那么x显然是没有右子树的，我们要实现将x移到原树的根上，也就是将x到根的这条链的深度全部翻转一遍，在辅助树上的体现就是将整棵树翻转一遍，我们可以写个翻转标记来减少复杂度。

代码实现：

inline void filp(int x){//Splay普通区间翻转
      swap(ch[x][0],ch[x][1]);r[x]^=1;
} 
inline void makeroot(int x){
      Access(x);
      Splay(x);
      filp(x);//懒标记&翻转区间
}

split(x,y)

这个操作是将x到y之间的那条路径丢到一棵辅助树里，并且这棵辅助树以y节点为根(方便处理信息)。

Splay 维护的是原树中的一条链，我们不能保证x,y会在同一条链里。

所以我们可以先把x变成原树的根节点(这下子Access(y)就会将x到y之间的所有节点丢到一个 Splay 中了)。

最后如上面所讲的，最后来一个 Splay(y) 就大功告成了。

代码实现：

inline void split(int x,int y){
      makeroot(x);Access(y);Splay(y);
}

link(x,y):

将x和y所在原树合并起来(链接)

首先将x点丢到原树的根，然后去找找y的根是不是x，如果不是说明x,y不在一个原树内，我们将x的父节点设为y，也就相当于从y到x连了一条虚边。

代码实现：

inline void link(int x,int y){
      makeroot(x);//丢到根
      if(findroot(y)!=x)f[x]=y;//链接一条虚边
//注意因为是虚边，所以不能认儿子
}

cut(x,y):

首先我们先把x,y之间的那条边用split(x,y)拎出来，因为x,y是相邻的，所以y的左儿子一定是x，将它们的父子关系消灭掉即可。

消灭父子关系时一定满足以下条件：

1.x和y在一个原树里(不在一个树里面往哪儿切啊)

2.split之后x是y的左儿子

3.x的右儿子是空的(保证了中序遍历中y紧跟在x的后面，即深度相邻)(x的权值(深度)只比y小1，而x又正好是直接连着y的，所以我们无法再找到 >x 而又 <y 的整数了)

代码实现：

inline void cut(int x,int y){
      split(x,y);
      if(findroot(y)==x&&f[x]==y&&!ch[x][1]){//判断各种条件
            f[x]=ch[y][0]=0;//彻底切断关系
            pushup(y);//儿子变了，更新
      }return;
}

0X03 Splay的改动：
旋转的改动：

这里需要注意一下，如果x的父亲节点的父亲节点y已经不在当前的这棵辅助树上，只需要连单向边(也就是虚边，认父不认子)，否则正常连就行，这里要和普通的rotate区分开来。

做个对比：

现在的rotate(x):

inline void rotate(int x){
      int y=f[x],z=f[y],k=chk(x),v=ch[x][!k]; 
      if(get(y))ch[z][chk(y)]=x;ch[x][!k]=y,ch[y][k]=v;
      if(v)f[v]=y;f[y]=x,f[x]=z;pushup(y),pushup(x);
}

普通的rotate(x):

inline void rotate(int x){
      int y=f[x],z=f[y],k=chk(x),v=ch[x][!k]; 
      ch[z][chk(y)]=x;ch[x][!k]=y,ch[y][k]=v;
      f[v]=y;f[y]=x,f[x]=z;pushup(y),pushup(x);
}

Splay的改动

同样要注意一下只能Splay到辅助树的根节点，Splay之前需先下传一下这一条链上需操作的所有的点，用栈来完成即可，可以手写栈来减少常数。

inline void Splay(int x){
      int y=x,top=0;hep[++top]=y;
      while(get(y))hep[++top]=y=f[y];
      while(top)pushdown(hep[top--]);

      while(get(x)){//基本普通的Splay
            y=f[x],top=f[y];
            if(get(y))
                  rotate((ch[y][0]==x)^(ch[top][0]==y)?x:y);
            rotate(x);
      }pushup(x);return; 
}

0X04 一些题目代码：
luogu P3690【模板】Link Cut Tree（动态树）(模板题)

就是上文讲的。

Code:

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define RI register int
#define A printf("A")
#define C printf(" ") 
using namespace std;
const int N=3e5+2;
template <typename Tp> inline void IN(Tp &x){
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9')if(ch=='-')f=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();x*=f;
}int f[N],v[N],s[N],r[N],hep[N],ch[N][2];
inline int get(int x){
    return ch[f[x]][0]==x||ch[f[x]][1]==x;
}
inline void pushup(int x){
    s[x]=s[ch[x][1]]^s[ch[x][0]]^v[x];
}
inline void filp(int x){
    swap(ch[x][0],ch[x][1]);r[x]^=1;
} 
inline void pushdown(int x){
    if(!r[x])return;r[x]=0;
    if(ch[x][0])filp(ch[x][0]);
    if(ch[x][1])filp(ch[x][1]);
} 
inline void rotate(int x){
    int y=f[x],z=f[y],k=ch[y][1]==x,v=ch[x][!k]; 
    if(get(y))ch[z][ch[z][1]==y]=x;ch[x][!k]=y,ch[y][k]=v;
    if(v)f[v]=y;f[y]=x,f[x]=z;pushup(y);
}
inline void Splay(int x){
    int y=x,top=0;hep[++top]=y;
    while(get(y))hep[++top]=y=f[y];
    while(top)pushdown(hep[top--]);
    while(get(x)){
        y=f[x],top=f[y];
        if(get(y))
           rotate((ch[y][0]==x)^(ch[top][0]==y)?x:y);
        rotate(x);
    }pushup(x);return; 
}
inline void Access(int x){
    for(register int y=0;x;x=f[y=x])
       Splay(x),ch[x][1]=y,pushup(x);
}
inline void makeroot(int x){
    Access(x);Splay(x);filp(x);
}
inline int findroot(int x){
    Access(x);Splay(x);
    while(ch[x][0])pushdown(x),x=ch[x][0];
    return x;
}
inline void split(int x,int y){
    makeroot(x);Access(y);Splay(y);
} 
inline void link(int x,int y){
    makeroot(x);if(findroot(y)!=x)f[x]=y;
}
inline void cut(int x,int y){
    makeroot(x);
    if(findroot(y)==x&&f[x]==y&&!ch[x][1]){
        f[x]=ch[y][0]=0;pushup(y);
    }return;
}int n,m,x,y,op;
int main(){
    scanf("%d%d",&n,&m);
    for(register int i=1;i<=n;++i)scanf("%d",&v[i]); 
    for(register int i=1;i<=m;++i){
        scanf("%d%d%d",&op,&x,&y);
        if(op==0)split(x,y),printf("%d\n",s[y]);
        else if(op==1)link(x,y);
        else if(op==2)cut(x,y);
        else Splay(x),v[x]=y;
    }return 0;
}

[SDOI2008]洞穴勘测

分析：题目只要求link(有一条新道路连接)和cut(道路被摧毁了cut)以及判断连通性(直接findroot，一样的话那么就是联通的)

就是LCT的板子，真的没那么难。

Code:

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define RI register int
#define A printf("A")
#define C printf(" ") 
using namespace std;
const int N=2e5+2;
template <typename Tp> inline void IN(Tp &x){
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9')if(ch=='-')f=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();x*=f;
}int n,m,f[N],r[N],hep[N],ch[N][2];
inline int get(int x){return ch[f[x]][0]==x||ch[f[x]][1]==x;}
inline void filp(int x){swap(ch[x][0],ch[x][1]);r[x]^=1;} 
inline void pushdown(int x){
    if(!r[x])return;r[x]=0;
    if(ch[x][0])filp(ch[x][0]);
    if(ch[x][1])filp(ch[x][1]);
}
inline void rotate(int x){
    int y=f[x],z=f[y],k=ch[y][1]==x,v=ch[x][!k]; 
    if(get(y))ch[z][ch[z][1]==y]=x;ch[x][!k]=y,ch[y][k]=v;
    if(v)f[v]=y;f[y]=x,f[x]=z;return; 
}
inline void Splay(int x){
    int y=x,top=0;hep[++top]=y;
    while(get(y))hep[++top]=y=f[y];
    while(top)pushdown(hep[top--]);
    while(get(x)){
        y=f[x],top=f[y];
        if(get(y))
           rotate((ch[y][0]==x)^(ch[top][0]==y)?x:y);
        rotate(x);
    }return; 
}
inline void Access(int x){
    for(register int y=0;x;x=f[y=x])
       Splay(x),ch[x][1]=y;
}
inline void makeroot(int x){
    Access(x);Splay(x);filp(x);
}
inline int findroot(int x){
    Access(x);Splay(x);
    while(ch[x][0])pushdown(x),x=ch[x][0];
    return x;
}
inline void split(int x,int y){
    makeroot(x);Access(y);Splay(y);
} 
inline void link(int x,int y){
    makeroot(x);if(findroot(y)!=x)f[x]=y;
}
inline void cut(int x,int y){
    makeroot(x);
    if(findroot(y)==x&&f[x]==y&&!ch[x][1]){
        f[x]=ch[y][0]=0;
    }return;
}char op[16];
int main(){
    scanf("%d%d",&n,&m);
    for(register int x,y,i=1;i<=m;++i){
    	scanf("%s%d%d",op,&x,&y);
        if(op[0]=='C')link(x,y);
        else if(op[0]=='D')cut(x,y);
        else if(op[0]=='Q'){
            if(findroot(x)==findroot(y))printf("Yes\n");
            else printf("No\n");
        }	
    }return 0;
}

再推存一道题目:P1501 [国家集训队]Tree II

这道题目主要就是懒标记的运用，建议在做这一道题之前先去做一做线段树的模板2，其实道理差不多，相通的，并不难。(讲乘法标记的正确下传方法弄到Splay的下传上即可)

当然这道题我也附上题解：题解 P1501【[国家集训队]Tree II】(Link-Cut-Tree)

0X05 致谢：
感谢FlashHu大佬的文章:LCT总结
感谢Menci大佬的文章：Link-Cut Tree 学习笔记
感谢学长quhengyi11的文章:LCT学习笔记
感谢tgop_knight大佬的文章：link-cut tree
感谢露迭月大佬的文章：Link Cat Tree(连喵树)学习笔记
鸣谢洛谷图床，方便我上传手绘图片!
最后推荐一个网址，这里面有一些基本的LCT例题以及作者的解析：传送门

posted @ 2019-01-01 10:56 babingbaboom 阅读(655) 评论(0) 编辑收藏举报

刷新页面返回顶部

Qiuly

梦想是要有的，万一实现了呢？

浅谈Link-Cut Tree(LCT)

0XFF 前言&概念

0X01 一些基本的定义

0X02 一些操作

Link-Cut Tree 支持以下几种基本操作：

Access(x):

findroot(x):

makeroot(x):

split(x,y)

link(x,y):

cut(x,y):

0X03 Splay的改动：

旋转的改动：

做个对比：

Splay的改动

0X04 一些题目代码：

luogu P3690【模板】Link Cut Tree（动态树）(模板题)

Code:

[SDOI2008]洞穴勘测

Code:

0X05 致谢：

感谢FlashHu大佬的文章:LCT总结

感谢Menci大佬的文章：Link-Cut Tree 学习笔记

感谢学长quhengyi11的文章:LCT学习笔记

感谢tgop_knight大佬的文章：link-cut tree

感谢露迭月大佬的文章：Link Cat Tree(连喵树)学习笔记

鸣谢洛谷图床，方便我上传手绘图片!

最后推荐一个网址，这里面有一些基本的LCT例题以及作者的解析：传送门

公告