数据结构--(AVL)平衡二叉树
AVL树本质上还是二叉树,但是比二叉搜索树多了一个条件:每个节点的左右子树高度不超过1
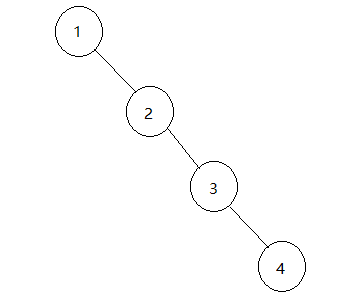
因为二叉搜索树在极端情况下无限趋近于链表,这种情况下不能体现二叉搜索树的高效率。如下图
AVL树定义及节点定义
public class AVLTree<T extends Comparable<T>>{
private Node<T> root;
class Node<T>{
private T key;
private Node<T> left;
private Node<T> right;
public Node(T key) {
this.key = key;
}
}
}
树的高度
public int height(){
return height(root);
}
private int height(Node<T> tree) {
if (tree == null) return 0;
else {
return Math.max(height(tree.left),height(tree.right))+1;
}
}
旋转
AVL树在添加或者删除后,可能导致AVL树失去平衡。
失去平衡包括四种:LL(左左),LR(左右),RR(右右),RL(右左),具体参考下图


LL旋转及代码
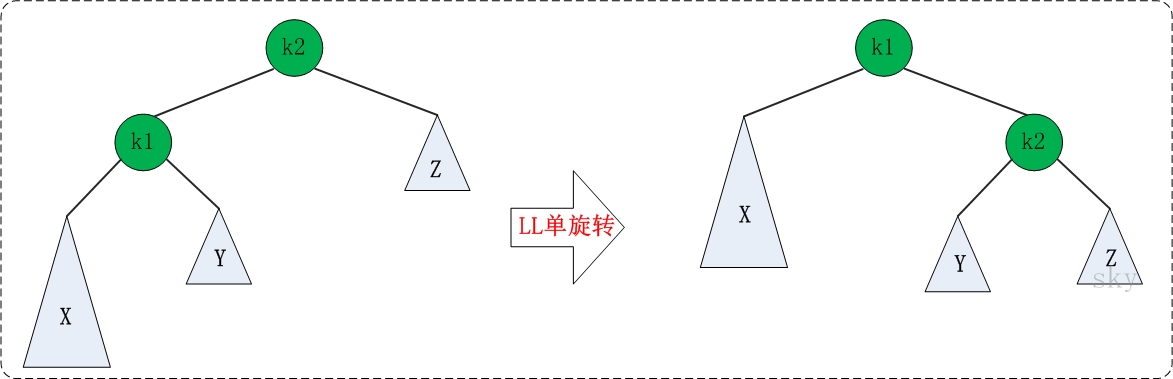
旋转方式:将k1变成根节点,k2变成k1的右子树,"k1的右子树"变成"k2的左子树"
/**
* 左左旋转
* @param tree
* @return
*/
private Node<T> llRotation(Node<T> tree){
Node<T> lTree = tree.left;
tree.left = lTree.right;
lTree.right = tree;
return lTree;
}
RR旋转及代码
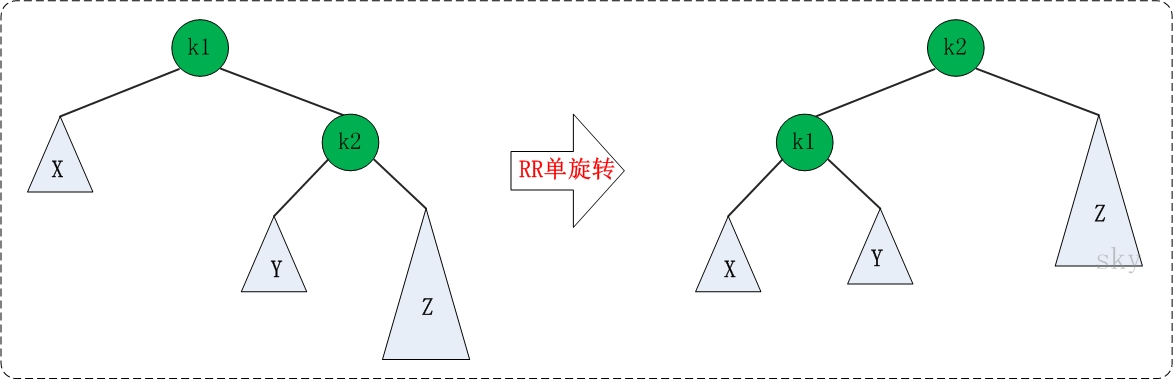
旋转方式:旋转方式与LL旋转类似
/**
* 右右旋转
* @param tree
* @return
*/
private Node<T> rrRotation(Node<T> tree){
Node<T> rTree = tree.right;
tree.right = rTree.left;
rTree.left = tree;
return rTree;
}
LR旋转及代码

旋转方式:左右旋转需要经过两次调整,第一次旋转是围绕"k1"进行的"RR旋转",第二次是围绕"k3"进行的"LL旋转"
/**
* 左右旋转
* @param tree
* @return
*/
private Node<T> lrRotation(Node<T> tree){
rrRotation(tree.left);
return llRotation(tree);
}
RL旋转及代码

旋转方式:右左旋转同样需要经过两次调整,第一次旋转是围绕"k3"进行的"LL旋转",第二次是围绕"k1"进行的"RR旋转"
/**
* 右右旋转
* @param tree
* @return
*/
private Node<T> rlRotation(Node<T> tree){
llRotation(tree.right);
return rrRotation(tree);
}
插入元素
public void add(T key){
if (root == null){
root = new Node<>(key);
}else {
add(root,key);//插入元素
root = fixAfterOperation(root);//插入元素后如果失去平衡则旋转
}
}
private Node<T> add(Node<T> tree, T key) {
int tmp;
if (tree == null){
tree = new Node<>(key);
}else {
tmp = key.compareTo(tree.key);
if (tmp < 0){
tree.left = add(tree.left,key);
}else if (tmp > 0){
tree.right = add(tree.right,key);
}else {
return tree;
}
}
return tree;
}
调整代码
当树添加或者删除某一节点后,如果导致AVL树失衡,旋转树
private Node<T> fixAfterOperation(Node<T> tree) {
if (tree != null) {
if (height(tree.left) - height(tree.right) == 2) {//如果左子树高度比右子树高度 高2,需要旋转
if (height(tree.left.left) > height(tree.left.right)) {//如果左子树的左子树比左子树的右子树高
tree = llRotation(tree);//左左旋转
} else {//如果左子树的左子树比左子树的右子树低
tree = lrRotation(tree);//左右旋转
}
}
if (height(tree.right) - height(tree.left) == 2) {//如果右子树高度比左子树高度 高2,需要旋转
if (height(tree.right.left) > height(tree.right.right)) {//如果右子树的左子树比右子树的右子树高
tree = rlRotation(tree);//右左旋转
} else {
tree =rrRotation(tree);//右右旋转
}
}
}
return tree;
}
删除元素
public void remove(T key){
if (root != null && key != null){
remove(root,key);
root = fixAfterOperation(root);
}
}
private Node<T> remove(Node<T> tree, T key) {
if (tree == null || key == null) return tree;
int tmp = key.compareTo(tree.key);
if (tmp < 0){
tree.left = remove(tree.left,key);
}else if (tmp > 0){
tree.right = remove(tree.right,key);
}else {
Node<T> successor = successor(tree);//获取后继节点
if (successor == null){//若后继节点为空,则删除节点的右子树为空
Node<T> l = tree.left;//查看左子树
if (l == null){//左子树为空,当前节点没有子节点
tree = null;
}else {//左子树不为空,当前节点值置为左子节点的值,然后删除左子树刚才替换节点值
tree.key = l.key;
tree.left = remove(tree.left,l.key);
}
}else {//后继节点不为空,则删除节点的值置为后继节点的值,然后在删除节点的右子树删除后继节点的值
tree.key = successor.key;
tree.right = remove(tree.right,successor.key);
}
}
return tree;
}
//获取后继节点
private Node<T> successor(Node<T> tree) {
Node<T> result = tree.right;
while (result != null && result.left != null){
result = result.left;
}
return result;
}