CFG 和 DFA 的交集为 CFG

起因是我队友问了我一个问题：

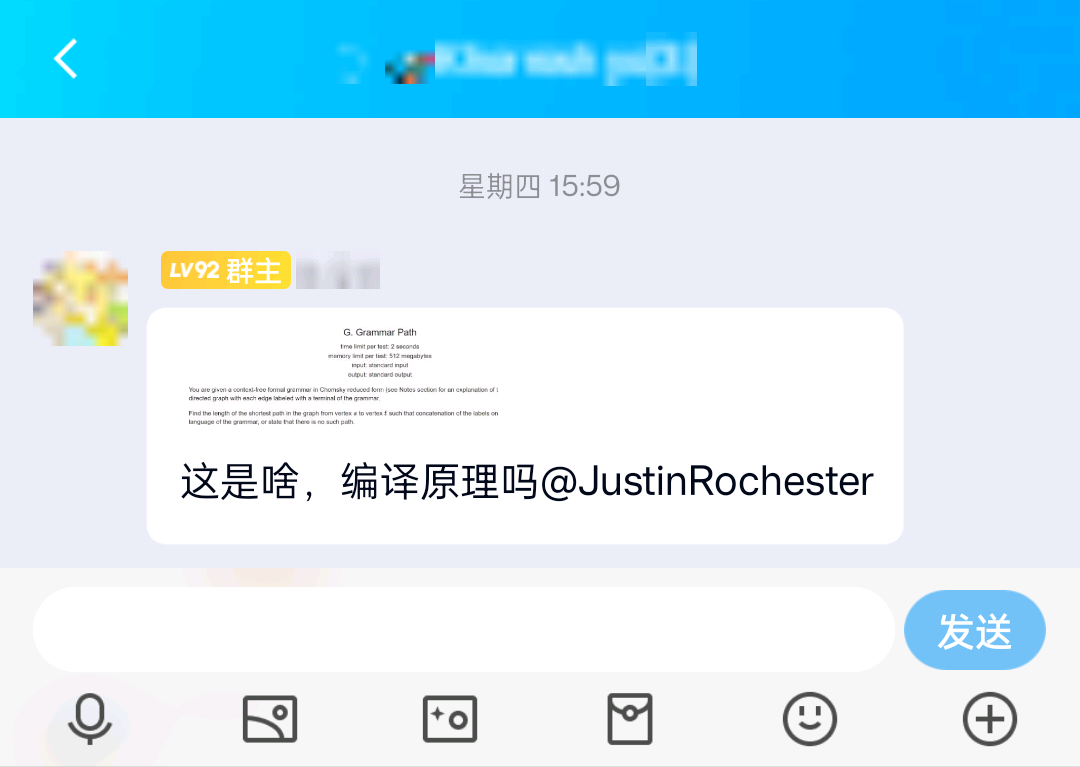
我后面看了一下那题，等价的题意是求一个 CFG 和 DFA 交集，能识别的最短串的长度。

虽然编译原理没学过，但是我在可计算理论上有学到过：有个结论是，CFG 和 DFA 的交集也是 CFG ；而 CFG 推导出的最短串可以用队列+贪心的方法求解。但并没有学过如何对于给定的 CFG 和 DFA，求出交集的 CFG。

我在国内某搜索引擎上并没有找到答案，最终在外网找到了一个比较靠谱的 文献 。所以我这篇笔记就是记录一下这个算法的流程。

定义

DFA

我们称一个确定型有穷状态自动机（Deterministic Finite Automaton, DFA）是一个五元组 ⟨Q,Σ,δ,q0,F⟩ ，其中五个参数依次为状态集、字符集、转移函数（δ:Q×Σ→Q）、起始状态和接收状态集。

在 DFA 的计算过程中，我们从初始状态 q0 出发，不断读入字符 c∈Σ ，并通过转移函数 δ(qi,c)=qi+1 不断更新状态。当读入完成后，若状态 qe∈F 则接受该读入，否则拒绝该读入。

对于一个 DFA M ，我们称所有能被 M 识别的字符串为 M 的语言 L(M) ，即 L(M)={s|δ(q0,s)∈F} 。

这里我们拓展了转移函数的意义：当字符串 s 的长度大于 1 时，我们将其划分为最后的字符 c 和前缀 t ，我们定义 δ(q,s)=δ(δ(q,t),c) 。

CFG

我们称一个上下文无关文法（Context-Free Grammer, CFG）是一个四元组 ⟨V,Σ,R,S⟩ ，其中五个参数依次为变元集、终结符集、产生式规则（R:V→(V∪Σ)∗）和起始变元。

其中，为了方便描述，产生式规则往往采用 A->BCdefG 的形式描述。其中产生式规则的左侧必须为变元。

在一个 CFG G 的计算过程中，我们从初始变元 S 出发，不断地选择当前串中的一个变元 A ，然后选择一个左侧为 A 的产生式规则进行替换：将 A 修改成产生式规则的右侧的串。

当我们将串推导成只含终结符的串 s 时，我们称该 CFG 接受串 s ，同理可定义语言 L(G)={s|S⇒+s∧(∀c∈s→c∈Σ)} 。

其中 ⇒ 符号表示推导，即上述使用产生式规则的一次替换过程；而 ⇒+ 符号表示若干正整数次的推导。

CNF

我们称一个 CFG 满足乔姆斯基范式（Chomsky Normal Form, CNF）指该 CFG 的产生式规则仅含有以下三种形式的产生式规则：

  1. 由起始变元推导出空串：S→ε
  2. 由一个变元推导出两个变元：A→BC
  3. 由一个变元推导出一个终结符：A→a

很显然，对于任何一个 CFG G ，必然存在 CNF G′ 使得 L(G′)=L(G)

CFG 可以模拟 DFA 的计算

我们常说 DFA 的描述能力是 CFG 描述能力的一个子集。即对于所有 DFA 语言构成的集合 S1 和所有 CFG 语言构成的集合 S2 必然有 S1⊂S2 。

经典的证明方法

一个比较经典的证明方法是，我们可以通过广义非确定型有穷状态自动机（Generalized Nondeterministic Finite Automaton, GNFA）将一个 DFA 转化成等价的正则语言 R 。

而我们众所周知：

  1. 空语言为正则语言。
  2. c 为正则语言（c∈Σ）。
  3. ε 为正则语言。
  4. 若 R1,R2 为正则语言，则 R1R2 为正则语言。
  5. 若 R1,R2 为正则语言，则 R1∪R2 为正则语言
  6. 若 R 为正则语言，则 (R) 为正则语言。
  7. 若 R 为正则语言，则 R∗ 为正则语言。

于是我们可以对于该正则语言 R 构造对应的 CFG：

  1. 若 L(R)=∅ 则产生式规则集合为 ∅ 。
  2. 若 L(R)={c},c∈Σ 则产生式规则集合为 {S→c} 。
  3. 若 L(R)={ε} 则产生式规则集合为 {S→ε} 。
  4. 若 R=R1R2 则分别构造 S1,S2 能表示 R1,R2 ，然后添加产生式 S→S1S2 。
  5. 若 R=R1∪R2 则分别构造 S1,S2 能表示 R1,R2 ，然后添加产生式 S→S1 和 S→S2。
  6. 若 R=(R1) 则构造 S1 表示 R1 ，然后添加产生式 S→S1 。
  7. 若 R=R1∗ 则构造 S1 表示 R1 ，然后添加产生式 S→S1S 和 S→ε 。

很显然，两者描述的是同一种语言。

比较特别的证明方法

但在那篇文献的思想里，其实我们有一种不通过正则语言中转的方法直接证明两者的能力关系：

当 DFA M=⟨Q,Σ,δ,q0,F⟩ 的接受状态集 F 是大小为 1 的集合 {f} 时，我们按如下方法构造一个 CFG G=⟨V,Σ,R,S⟩ ：

首先，DFA 的字符集和 CFG 的终结符集是同一个集合，而变元集 V 我们定义为 Q×Q∪{S} ，起始变元为 S ，产生式规则定义如下：

  1. ∀x,y,z∈Q ，向 R 中添加规则 ⟨x,y⟩→⟨x,z⟩⟨z,y⟩ 。
  2. ∀x∈Q,c∈Σ ，向 R 中添加规则 ⟨x,δ(x,c)⟩→c 。
  3. ∀x∈Q ，向 R 中添加规则 ⟨x,x⟩→ε 。
  4. 向 R 中添加规则 S→⟨q0,f⟩ 。

这看起来很奇怪，但实际上它描述的语言也和 M 等价。一个比较好的理解方法是：变元 ⟨u,v⟩ 描述的是状态 u 读入一些字符串后会转移到 v 状态，而该变元能推导出所有满足这条件的字符串。

而对于多接受状态的 DFA M ，一个方法是将其拆解为多个单接收状态的 DFA，分别产生上述的 S1,S2,S3,⋯ 后，再通过引入 S→S1,S→S2,S→S3,⋯ 进行合并。

另一个更为简便的方法是，直接修改最后一个规则为：∀f∈F ，向 R 中添加规则 S→⟨q0,f⟩ 。

CFG 和 DFA 的交集为 CFG

经过这个比较特别的证明方法后，这一步的理解会变得更为简单。我们同样是考虑一个 DFA M=⟨Q,Σ,δ,q0,F⟩ 和一个 CFG G0=⟨V0,Σ,R0,S0⟩ 。这里，我们直接假设 G0 的一个 CNF，若不满足，可以进行转化。

同样的，当 DFA 的接受状态集 F 是大小为 1 的集合 {f} 时，我们按如下方法构造一个 CFG G=⟨V,Σ,R,S⟩ ：

首先，M 的字符集和 G,G0 的终结符集仍是同一个集合，而变元集 V 我们定义为 Q×V0×Q∪{S} ，起始变元为 S ，产生式规则定义如下：

  1. 对于 G0 的一个产生式规则 A→BC ，我们对 ∀x,y,z∈Q ，向 R 中添加规则 ⟨x,A,y⟩→⟨x,B,z⟩⟨z,C,y⟩ 。
  2. 对于 G0 的一个产生式规则 A→c,c∈Σ ，我们对 ∀x∈Q ，向 R 中添加规则 ⟨x,A,δ(x,c)⟩→c 。
  3. 若 G0 存在产生式规则 S0→ε 且 q0∈F ，则向 R 中添加规则 ⟨q0,S0,q0⟩→ε 。
  4. 向 R 中添加规则 S→⟨q0,S0,f⟩ 。

参考上述的理解方法，变元 ⟨u,A,v⟩ 描述的其实是从状态 u 出发，读入了一些能规约成 A 变元的字符串，转移到 v 状态，这个变元能推导出所有满足该条件的字符串。

从该理解角度，证明的正确性十分显然。

最后，对于多接收状态的 DFA，可以像上文方法直接进行拆解后，通过引入新产生式进行合并；也可以类似上述方法，直接修改最后一个规则为：∀f∈F ，向 R 中添加规则 S→⟨q0,S0,f⟩ 。

posted @   JustinRochester  阅读(246)  评论(0)  编辑  收藏  举报
相关博文：
· 题解 G. Grammar Path 2020-2021 ICPC NERC (NEERC)
· 快速傅里叶变换（FFT）的分治实现
· 证明正则语言和上下文无关语言的交集还是一个上下文无关语言
· C# 词法分析器（五）转换 DFA update 2022.09.11
· CS3231 Theory of Computation 归档
阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· Manus爆火，是硬核还是营销？
· 终于写完轮子一部分：tcp代理 了，记录一下
· 别再用vector＜bool＞了！Google高级工程师：这可能是STL最大的设计失误
· 单元测试从入门到精通
历史上的今天：
2020-02-04 题解 P1447 【[NOI2010]能量采集】
点击右上角即可分享
微信分享提示