复数的运算性质和几何性质

本文作者为 JustinRochester。

目录地址

上一篇

下一篇

---

复数的运算性质和几何性质

虚数的来源

我们考虑一个递推方程：\(f_n= \begin{cases} \begin{aligned} 2f_{n-1}-2f_{n-2}&,n\geq 2\\ n&,n\in\{0, 1\}\\ \end{aligned} \end{cases}\) 。我们可以递推出这个方程的前几项：

\(n\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(f_n\)	\(0\)	\(1\)	\(2\)	\(2\)	\(0\)	\(-4\)

同时，我们可以通过特征方程法求出通项公式：\(\displaystyle f_n={(1+\sqrt{-1})^n-(1-\sqrt{-1})^n\over 2\sqrt{-1}}\)

很可惜，方程中涉及到了 \(\sqrt{-1}\) ，它在实数上是无解的。然而，假设我们将 \(\sqrt{-1}\) 当成一个单独的变元，计算后再通过 \((\sqrt{-1})^2=-1\) 可以重新得到上述的递推结果。例如：

\(\begin{aligned} f_5&={(1+\sqrt{-1})^5-(1-\sqrt{-1})^5\over 2\sqrt{-1}}\\ &={[1+5\sqrt{-1}+10(\sqrt{-1})^2+10(\sqrt{-1})^3+5({\sqrt{-1}})^4+({\sqrt{-1}})^5]-[1-5\sqrt{-1}+10(\sqrt{-1})^2-10(\sqrt{-1})^3+5({\sqrt{-1}})^4-({\sqrt{-1}})^5]\over 2\sqrt {-1}}\\ &={2[5\sqrt{-1}+10({\sqrt{-1}})^3+({\sqrt{-1}})^5]\over 2\sqrt{-1}}\\ &=5+10(\sqrt{-1})^2+(\sqrt{-1})^4 \end{aligned}\)

我们代入 \((\sqrt{-1})^2=-1\) 得到： \(f_5=5+10\cdot (-1)+(-1)^2=-4\) ，这和我们递推得到的结果一致。

这启示我们，\(\sqrt{-1}\) 是一个具有数学意义的单位。我们将其记为 \(i=\sqrt{-1}\) ，并命名为虚数，方便我们进一步研究它的性质。

---

复数的定义和四则运算

我们称，形如 \(z=a+bi(a,b\in R, i=\sqrt{-1}, \text{ 下同})\) 的数字为虚数，其中必须满足 \(b\neq 0\) ，否则式子将退化为实数。

我们统称虚数（imaginary number）和实数（real number）为复数（complex number），因此复数的形式同上式一致，但不必满足 \(b\neq 0\) 条件。我们记复数集为字母 \(C\) 。

对于复数 \(z=a+bi\)，我们称 \(a\) 为它的实部，记为 \(\Re z=a\) 或 \(\text{Re }a\)；同理，称 \(b\) 为它的虚部，记为 \(\Im z=b\) 或 \(\text{Im }b\)。

我们称实部相同，虚部互为相反数的两个复数互为共轭复数。对于复数 \(z=a+bi\) ，我们记它的共轭复数 \(\bar z=a-bi\) 。

于是，根据定义，我们可以很快定义两个复数的加减乘三个运算：

\(z_1=a_1+b_1i,z_2=a_2+b_2i\)

则 \(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\)

而 \(z_1\cdot z_2=a_1a_2+(a_1b_2+a_2b_1)i+b_1b_2i^2=a_1a_2+(a_1b_2+a_2b_1)i-b_1b_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\)

对于除法，我们想直接写成上述的形式则比较困难了。有什么办法解决呢？

首先，我们观察一下，两个共轭复数的乘积会有什么特点：

\(z_2\cdot \bar{z_2}=(a_2a_2+b_2b_2)+(-a_2b_2+a_2b_2)i=a_2^2+b_2^2\in R\)

因此，当我们计算 \({z_1\over z_2}\) 时，我们往往会分子分母同乘一个 \(\bar z_2\) 使得分母实数化。如若需要展开来写，则是：

\(\displaystyle {z_1\over z_2}={z_1\cdot \bar{z_2}\over z_2\cdot \bar{z_2}}={(a_1a_2+b_1b_2)+(-a_1b_2+a_2b_1)i\over a_2^2+b_2^2}={a_1a_2+b_1b_2\over a_2^2+b_2^2}+{-a_1b_2+a_2b_1\over a_2^2+b_2^2}i\)

我们可以发现，复数在加减乘除的运算下，得到的答案仍然是复数；即复数和实数一样，在四则运算下是封闭的。

但是这仍然有个问题：实数在开方运算下不封闭，例如 \(-1\) 开平方运算后得到了 \(\sqrt{-1}=i\not\in R\) ，复数能满足这个要求吗？

若 \(\sqrt{i}\not\in C\) ，我们还需要定义“复复数”、“复复复数”、......这样的递归定义将显得非常鸡肋。

---

复数四则运算的几何性质

我们观察到，复数的加减法运算和二维直角坐标系上的向量的加减法运算形式一致。这启示我们，会不会复数的四则运算和二维直角坐标系上的一些几何性质相关。

显然，当复数进行加减法时，若 \(z_1=a_1+b_1i,z_2=a_2+b_2i\) 则 \(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\) ；它等价于向量 \(\boldsymbol v_1=(a_1,b_1)^T\) 与向量 \(\boldsymbol v_2=(a_2,b_2)^T\) 进行加减法 \(\boldsymbol v_1\pm \boldsymbol v_2=(a_1\pm a_2, b_1\pm b_2)^T\) 。

但很可惜，二维向量并没有定义从两个二维向量到一个二维向量的乘法运算。因此，我们需要重新观察复数乘法的几何性质。

我们取两个复数 \(z_1=\sqrt 3+3 i, z_2=\sqrt 3+i\) ，两个向量的复数为 \(z=z_1\cdot z_2=4\sqrt 3i\) 。

这时候，我们如果在二维直角坐标系上画出三个向量，进行观察，会发现两个特殊的性质：

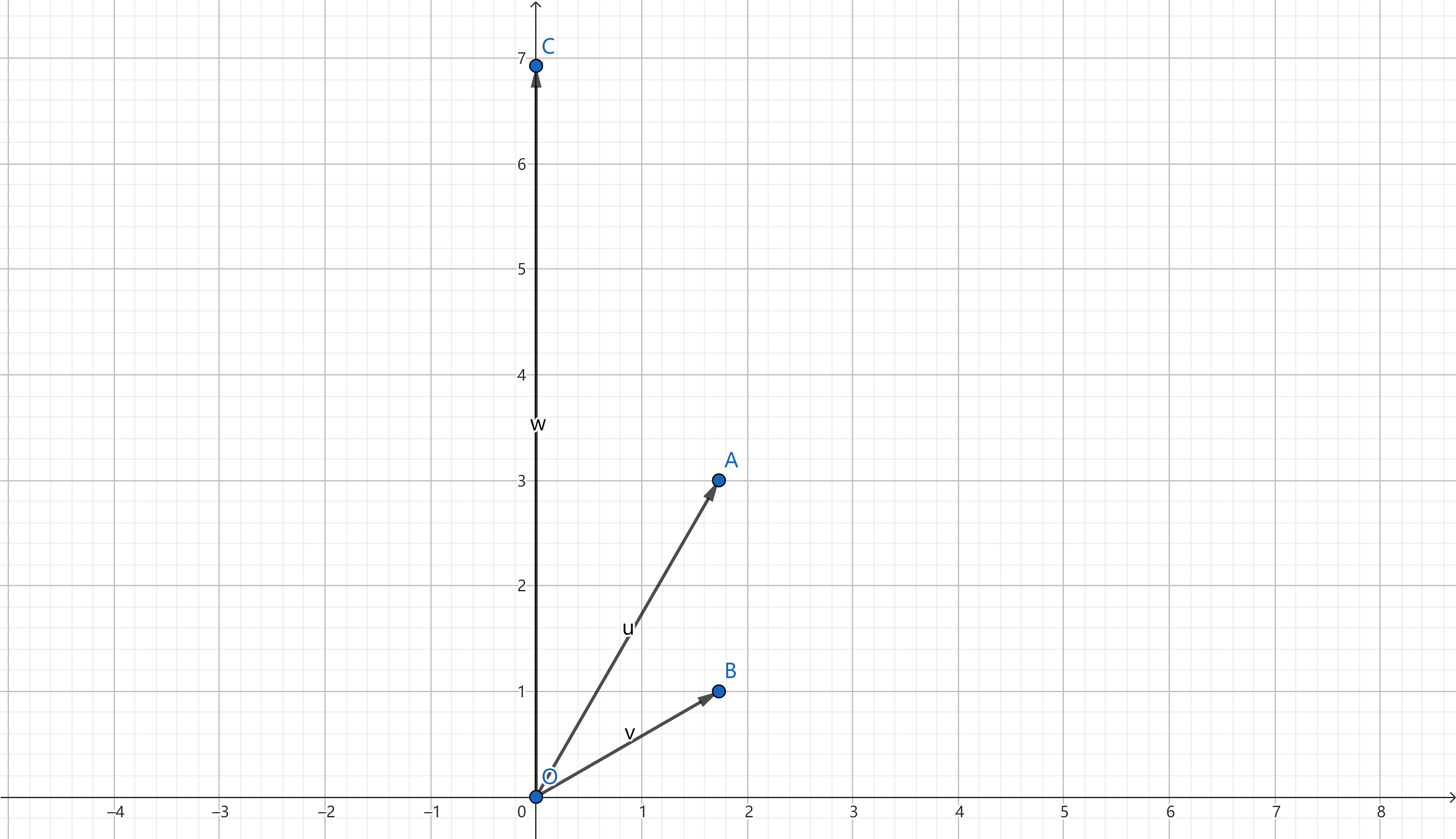
第一个向量的一个幅角（即从 \(x\) 正半轴逆时针旋转到向量的角度）为 \({\pi\over 3}\) ，第二个为 \({\pi\over 6}\) ，第三个为 \({\pi\over 2}\) 。而 \({\pi\over 2}={\pi\over 3}+{\pi\over 6}\) 。

此外，第一个向量的模长（即从原点到向量端点的长度）为 \(2\sqrt{3}\) ，第二个为 \(2\) ，第三个为 \(4\sqrt {3}\) 。而 \(4\sqrt{3}=2\sqrt{3}\cdot 2\) 。

似乎两个复数的乘积满足幅角相加和模长相乘两个性质。这是否是真的呢？

为了证明这个性质，首先我们对于向量 \(z=a+bi\) ，定义其模长 \(|z|=\sqrt{a^2+b^2}\) ，定义其幅角 \(\arg(z)=2k\pi+\text{Arg}(z)= \begin{cases} \begin{aligned} 2\arctan{b\over \sqrt{a^2+b^2}+a}&,b\neq 0\\ 0&,b=0\wedge a>0\\ \pi&,b=0\wedge a<0\\ \end{aligned} \end{cases},k\in Z\) 。为了方便描述，我们定义主幅角 \(\text{Arg}(z)\) 为 \(\arg(z)\) 中，位于 \((-\pi,\pi]\) 范围的那一个取值。

当两个复数 \(z_1=a_1+b_1i, z_2=a_2+b_2i\) 乘法得到 \(z=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\) 时：

\(\begin{aligned} |z|^2&=(a_1a_2-b_1b_2)^2+(a_1b_2+a_2b_1)^2\\ &=a_1^2a_2^2+b_1^2b_2^2+a_1^2b_2^2+a_2^2b_1^2-2a_1a_2b_1b_2+2a_1b_2a_2b_1\\ &=a_1^2(a_2^2+b_2^2)+b_1^2(a_2^2+b_2^2)\\ &=(a_1^2+b_2^2)(a_2^2+b_2^2)\\ &=|z_1|^2\cdot |z_2|^2\\ \end{aligned}\)

幅角也类似上述的方式，通过分类讨论可以得出复数相乘幅角相加的结论。这里碍于篇幅，便不展开叙述了。

因此，我们知道了，复数乘法时，模长相乘、幅角相加；复数相除时，模长相除、幅角相减。

正向3B1B在视频里表示的那样，实数中，加减法表示数轴的平移，乘除法表示数轴的缩放；复数中，加减法表示数轴的平移，乘除法表示数轴的缩放与旋转。

---

复数的极坐标形式

我们原来的复数表示法是二维直角坐标系下的表现形式。然而我们知道，二维直角坐标系下的点可以唯一地表示为一个二维极坐标的形式。而二维极坐标的极径恰好可以表示复数的模长，极角恰好可以表示复数的幅角。这启示我们复数能否有一个极坐标意义下，等价的表现形式。

我们知道，指数可以将乘除法化为加减法。于是我们考虑，能否用 \(r\cdot C^{\theta}\) 的方法表示一个复数，其中 \(r\in R\wedge r\geq 0, C\) 为一常数。

这样，复数就可以直接用模长和幅角进行表示，此时若 \(\displaystyle z_1=r_1\cdot C^{\theta_1}, z_2=r_2\cdot C^{\theta_2}\) 则 \(\displaystyle z_1\cdot z_2=(r_1\cdot r_2)\cdot C^{\theta_1+\theta_2}, {z_1\over z_2}={r_1\over r_2}\cdot C^{\theta_1-\theta_2}\) ，符合了复数乘法的要求。

很幸运，这个常数被欧拉找到了。根据欧拉公式：\(e^{i\theta}=\cos\theta+i\sin\theta\) 。

一个很著名的推论为 \(e^{i\pi}=\cos\pi+i\sin\pi=-1+i\cdot 0=-1\iff e^{i\pi}+1=0\)

所以我们找到了这个常数 \(C=e^i\) 。于是我们也可以用 \(z=re^{i\theta}\) 的形式表示一个复数，我们称之为复数的极坐标形式。

显然，复数的笛卡尔坐标形式和复数的极坐标形式是可以互转的。

---

复数的初等函数运算

根据复数的极坐标形式，我们很快就能推广复数的初等函数运算：

对于幂函数，我们对于复数 \(z=re^{i\theta}\) ，我们定义其 \(k\) 次幂为 \(c=r^ke^{i(k\theta)}\) 。

当然，当 \(k\) 不为整数时，会有一些问题：

因为实际上复数的幅角有无穷多个，每个之间都相差一个 \(2\pi\) 的整数倍。所以，当 \(k\) 不为整数时，可能会导致运算后，落在 \((-\pi, \pi]\) 范围内复数并不止一个。这虽然有点反直觉，但复数上的幂函数值确实是多值的。

例如 \(i=1\cdot e^{i({\pi\over 2}+2k\pi)}\) 则 \(\sqrt{i} = \sqrt{1}\cdot e^{i({\pi\over 4}+k\pi)}=1\cdot e^{i({\pi\over 4}+2k\pi)}\) 或 \(1\cdot e^{i({5\pi\over 4}+2k\pi)}={\sqrt 2\over 2}+{\sqrt 2\over 2}i\) 或 \(-{\sqrt 2\over 2}-{\sqrt 2\over 2}i, k\in Z\) 。

一个理解方法是，复数在进行初等函数运算的时候，是一个复数的集合，通过函数生成另一个复数的集合。这样就避免了函数多值的问题。

这也解释了上述的问题，复数的开方运算结果是复数，它在开方运算下也是封闭的。不存在所谓的“复复数”。

而关于复数的极坐标形式，若其模长不为 \(0\) ，则 \(z=e^{\ln r} e^{i\theta}=e^{\ln r+\theta i}\) ，于是我们就得到了复数的对数函数结果：

\(\ln z=\ln r+(\theta+2k\pi)i,k\in Z\) 。

同理也有复数的指数运算：当 \(z=a+bi\) 时

\(\exp z=e^a\cdot e^{bi}=e^a\cos b+e^a\sin b \cdot i\)

关于三角函数，我们根据 \(e^{i\theta}=\cos\theta+i\sin\theta\) 可以通过指数函数和消元法，得到：

\(\cos\theta={e^{i\theta}+e^{-i\theta}\over 2}=\cosh i\theta, \sin\theta={e^{i\theta}-e^{-i\theta}\over 2i}=-i\sinh i\theta\)

于是我们可以通过这个方法定义出其他的三角函数和反三角函数。于是复数的初等函数运算都已定义完毕。

可以发现，复数确实是一个很好的数系，在各个初等函数内进行运算，都是封闭的。

---

例题

2022杭电多校6 1009.Map

大意

给定一张地图的四角，将它缩小并旋转后，放回原地图内部。现给定变换前后地图四角的八个坐标，求变化后坐标没变化的点。

分析

缩小旋转这样的操作刚好可以用复数的乘法进行描述。

我们称原地图的四角为复数 \(ABCD\) 而变换后的为复数 \(abcd\) ，不变点为 \(P\) 。

我们将不变点平移到坐标原点，则所有点的变换方向都一致了，可以用一个复数 \(z\) 表示。于是有：

\(\begin{cases} \begin{aligned} a-P&=&z(A-P)\\ b-P&=&z(B-P)\\ c-P&=&z(C-P)\\ d-P&=&z(D-P)\\ \end{aligned} \end{cases}\)

随便挑两个方程（例如前两个）对除一下，则消去了 \(z\) ，得到：

\(\displaystyle {a-P\over b-P}={A-P\over B-P}\)

再交叉相乘得到：

\(aB+P^2-(a+B)P=Ab+P^2-(A+b)P\)

\(P={Ab-aB\over A+b-a-B}\)

于是我们实现一下复数的乘除法就可以得到答案了。

#include <bits/stdc++.h>
using namespace std;
typedef long double db;
struct vir {
	db r, i;
	inline vir(db r_=0, db i_=0):r(r_), i(i_) {}
	inline db len2() const { return r*r+i*i; }
	inline db len() const { return sqrtl(r*r+i*i); }
	inline db arg() const { return atan2l(i, r); }
	
	inline vir& operator += (const vir &x) {
		r+=x.r; i+=x.i;
		return *this;
	}
	inline vir& operator -= (const vir &x) {
		r-=x.r; i-=x.i;
		return *this;
	}
	inline vir& operator *= (const vir &x) {
		tie(r, i) = make_pair(
			r*x.r-i*x.i,
			r*x.i+i*x.r
		);
		return *this;
	}
	inline vir& operator /= (const vir &x) {
		db l=x.len2();
		tie(r, i) = make_pair(
			(r*x.r+i*x.i)/l,
			(-r*x.i+i*x.r)/l
		);
		return *this;
	}
	
	inline vir operator ! () const { return vir(r, -i); }
	inline vir operator + (const vir &x) const { vir y=*this; return y+=x; }
	inline vir operator - (const vir &x) const { vir y=*this; return y-=x; }
	inline vir operator * (const vir &x) const { vir y=*this; return y*=x; }
	inline vir operator / (const vir &x) const { vir y=*this; return y/=x; }
	
	inline friend istream& operator >> (istream& in, vir &v) { return in>>v.r>>v.i; }
	inline friend ostream& operator << (ostream& out, const vir &v) { return out<<v.r<<" "<<v.i; }
};
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cout<<fixed<<setprecision(9);
	int T; cin>>T;
	while(T--) {
		vir A, B, C, D, a, b, c, d;
		cin>>A>>B>>C>>D;
		cin>>a>>b>>c>>d;
		cout<<(A*b-a*B)/(A+b-a-B)<<"\n";
	}
	return 0;
}