The 19th Zhejiang Provincial Collegiate Programming Contest - J. Frog 题解
【大意】
在平面直角坐标系的原点上,放置一个半径为 \(1\) ,不可穿透的圆柱体。
一只青蛙需要从坐标 \((\cos ({d_s\over 180}\cdot \pi), \sin ({d_s\over 180}\cdot \pi))\) 处跳跃到 \((\cos ({d_t\over 180}\cdot \pi), \sin ({d_t\over 180}\cdot \pi))\) 处,且每一步的距离必须严格为 \(1\) 。
求最少步数,并输出方案。
【分析】
由于涉及到两个角度,我们不妨通过旋转,消除其中一个:将整个坐标系顺时针旋转 \(\theta_s={d_s\over 180}\cdot \pi\) 个弧度,最后计算答案的时候再逆回去,等价于左乘一个 \(M_0=\left(\begin{matrix}\cos\theta_s&-\sin\theta_s\\\sin\theta_s&\cos\theta_s\end{matrix}\right)\) 。
这下问题等价于从 \((1,0)\) 跳至 \((\cos ({d_t-d_s\over 180}\cdot \pi), \sin ({d_t-d_s\over 180}\cdot \pi))\) 处。
而题目要求步数最少,故当角度差值大于 \(180^\circ\) 时,答案等价于小于 \(180^\circ\) 的答案翻转得到。
故,若 \((d_t-d_s\bmod 360)>180\) 时,将 \(y\) 翻转,等价于先左乘一个 \(M_1=\left(\begin{matrix}1&0\\0&-1\end{matrix}\right)\),再左乘一个 \(M_0\) 。此时 \(M_0M_1=\left(\begin{matrix}\cos\theta_s&-\sin\theta_s\\-\sin\theta_s&-\cos\theta_s\end{matrix}\right)\) 。
现在,我们只要解决从 \((1, 0)\) 跳至 \((\cos\theta, \sin\theta)\) 处的问题即可,\(0\leq \theta\leq \pi\)。只要将过程中的每个点 \((x, y)\) 输出前,进行 \(M\) 的逆变换还原原坐标即可。
不难,对于当 \(\theta=0\) 的时候,步数为 \(0\) 。
而当 \(\theta>0\) 时,由于圆柱体不可跨越,不可能从圆柱边缘一点,跳跃至令一点。故不存在步数为 \(1\) 的解。
同时,为了保证跳跃过程中不会穿过圆柱,我们需要保证起始的方向起码要与圆柱相切(可以更外)。
很容易想到,当 \(\theta\leq {\pi\over 2}\) 时,存在路径 \((1, 0)\to(1+\cos\theta, \sin\theta)\to(\cos\theta, \sin\theta)\) ,长度为 \(2\) 。
再根据样例中 \(\theta=\pi\) 时需要 \(4\) 步,也很容易构造。对于 \(\theta>{\pi\over 2}\) 时,必然存在路径 \((1, 0)\to(1, 1)\to(0, 1)\to(\cos\theta, 1+\sin\theta)\to(\cos\theta, \sin\theta)\) ,长度为 \(4\) 。
剩下的问题就是,确认是否在 \(\theta>{\pi\over 2}\) 时,存在步数为 \(3\) 的路径。
直观上,我们会觉得,存在一条路径关于 \({\theta\over 2}\) 对称。
不妨假设路径如下所示:
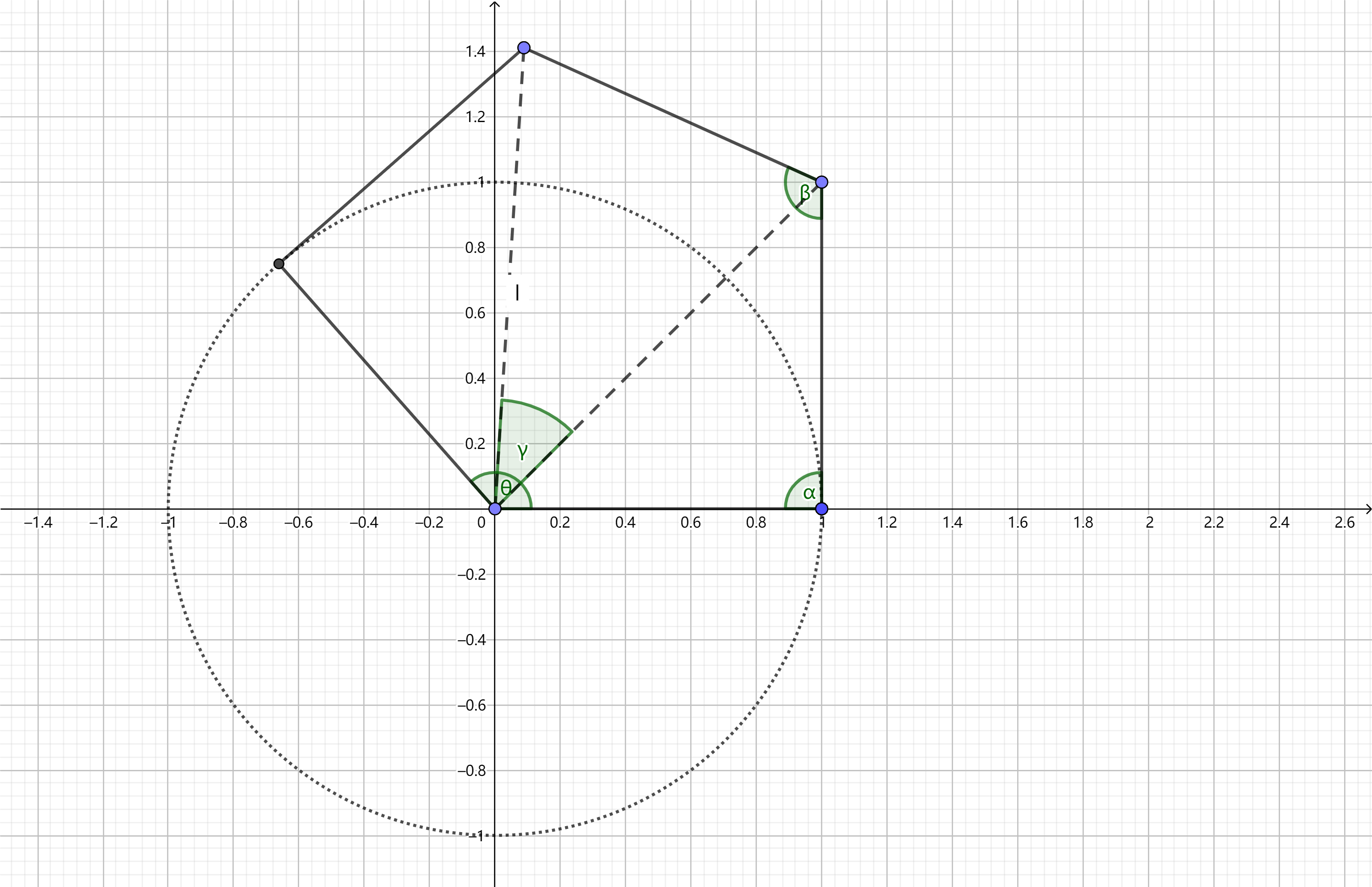
根据图上几何关系,显然有 \(\theta+2\alpha+2\beta=3\pi, \theta\in({\pi\over 2}, \pi], \alpha\in[{\pi\over 2}, \pi]\) 。
于是有 \(\gamma=\theta-2\cdot {\pi-\alpha\over 2}=\theta+\alpha-\pi\) (等腰三角形性质)。
由于每条边都是 \(1\) ,对 \(\alpha\) 用余弦定理得 \(l^2=1^2+1^2-2\cdot 1\cdot 1\cdot \cos\alpha=2(1-\cos\alpha)\) 。
再对 \(\gamma\) 用余弦定理得 \(1^2=l^2+l^2-2\cdot l\cdot l\cdot \cos\gamma=2l^2(1-\cos\gamma)\) 。
代入整理得到 \((1-\cos\alpha)(1+\cos(\theta+\alpha))={1\over 4}\) 。
直观上我们发现,\(\alpha\) 越接近 \({\pi\over 2}\) ,\(\theta\) 越大。
故代入得到 \(\alpha={\pi\over 2}\) 时,\(\sin \theta={3\over 4}\) 。由于 \(\theta>{\pi\over 2}\) ,故 \(\theta=\pi-\arcsin{3\over 4}\approx 131.4^\circ\) 。
利用半角公式展开得到 \(\sin^2{\alpha\over 2}\cos^2{\theta+\alpha\over 2}={1\over 16}\) 。
注意到 \(\sin{\alpha\over 2}>0\wedge \cos{\theta+\alpha\over 2}<0\) ,故 \(\sin{\alpha\over 2}\cos{\theta+\alpha\over 2}=-{1\over 4}\) 。
再由积化和差公式得到 \(-{1\over 4}={1\over 2}(\sin(\alpha+{\theta\over 2})-\sin{\theta\over 2})\) 。
即 \(\sin(\alpha+{\theta\over 2})-\sin{\theta\over 2}=-{1\over 2}\) 。
由于 \(\alpha+{\theta\over 2}>{\pi\over 2}\) 。因此,对于确定的 \(\theta\) ,有 \(\alpha=\pi-\arcsin(\sin{\theta\over 2}-{1\over 2})-{\theta\over 2}\) 。
于是我们得到结论:当角度差值不超过 \(131\) 时,存在 \(3\) 步路径,否则为 \(4\) 步。
且第一步落脚点为 \((1+\cos(\pi-\alpha), \sin(\pi-\alpha))=(1-\cos\alpha, \sin\alpha)\) 。
第二步落脚点为 \((1-\cos\alpha, \sin\alpha)+(\cos(\pi-\beta+(\pi-\alpha)), \sin(\pi-\beta+(\pi-\alpha)))\) 。
即 \((1-\cos\alpha, \sin\alpha)+(\cos(\alpha+\beta), -\sin(\alpha+\beta))\) 。
其中,\(\beta={3\pi-\theta\over 2}-\alpha\) 。
【代码】
#include <bits/stdc++.h>
using namespace std;
#define de(x) cout << #x <<" = "<<x<<endl
#define dd(x) cout << #x <<" = "<<x<<" "
typedef long double db;
const db pi = acosl(-1);
const int lim=131;
db a11, a12, a21, a22;
inline void printxy(db x, db y) {
cout<<a11*x+a12*y<<" "<<a21*x+a22*y<<"\n";
}
inline void work() {
int ds, dt;
cin>>ds>>dt;
a11=cosl(pi*ds/180), a21=sinl(pi*ds/180), a12=-a21, a22=a11;
dt=(dt-ds+360)%360;
ds=0;
if(dt>180) {
a12=-a12;
a22=-a22;
dt=360-dt;
}
if(!dt) {
cout<<"0\n";
printxy(1, 0);
return ;
}
db theta=dt*pi/180;
if(dt<=90) {
cout<<"2\n";
printxy(1, 0);
printxy(1+cosl(theta), sinl(theta));
printxy(cosl(theta), sinl(theta));
return ;
}
if(dt>lim) {
cout<<"4\n";
printxy(1, 0);
printxy(1, 1);
printxy(0, 1);
printxy(cosl(theta), sinl(theta)+1);
printxy(cosl(theta), sinl(theta));
return ;
}
db alpha=pi-asinl(sinl(theta/2)-1.0/2)-theta/2;
db beta=pi*3/2-alpha-theta/2;
cout<<"3\n";
db nowx=1, nowy=0;
printxy(nowx, nowy);
nowx+=-cosl(alpha);
nowy+=sinl(alpha);
printxy(nowx, nowy);
nowx+=cosl(alpha+beta);
nowy+=-sinl(alpha+beta);
printxy(nowx, nowy);
printxy(cosl(theta), sinl(theta));
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cout<<fixed<<setprecision(9);
int T; cin>>T;
while(T--)
work();
cout.flush();
return 0;
}




