图论-链式前向星

学习笔记-链式前向星

作为一个学习OI刚刚两个月出头的蒟蒻，我的学习来源有一半都来自一本通教材，但是一本通里关于图论只重点介绍了邻接矩阵的存图方式，邻接表只提了一笔，然而在OI时最常用的是链式前向星方法

邻接矩阵

存图原理

开二维数组，a[x][y]表示从x到y的边。如果没有边权，0表示断1表示通。如果有边权，INF表示断，反之输入边权。对于无向图，把一条边当成来回两条边处理

例

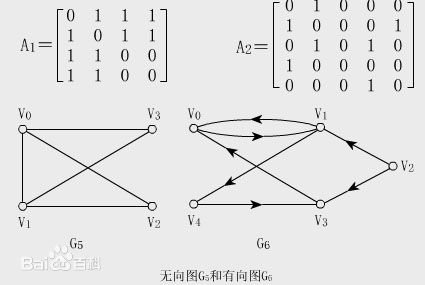
所以这种存图虽然易于理解，但是缺点显而易见，那就是空间是n²一定会炸，那么我们就需要学习▼

链式前向星

边的存储

这种存图方式只需要开一个数组存储每个点引出的第一条边，然后存储每个点作为起点的每条边，这样就可以做到不重不漏。所以代码是这样的

struct EDGE {//上一条边next同起点下一条边to终点w权值 
    int next;
    int to;
    int w;
};
EDGE edge[MAXM];
int head[MAXN];//head[i]为i点的第一条边 
int cnt=0;//存边时记录当前存了多少条边
void Add(int u, int v, int w) {//uvw起点终点权值 
    edge[++cnt].next = head[u];//更新cnt
    edge[cnt].to = v;
    edge[cnt].w = w;
    head[u] = cnt;
}

 

 注意：这里的next指的是遍历时的下一条边，head指的是遍历时的第一条边，而存边时相当于反过来操作，所以next记录上一条边，而head记录最后一条边。

边的遍历

这样，在遍历以x为起点的所有边时，只需要这样就行

for( int i = head[x]; i != 0; i = edge[i].next)

这个循环的结束条件是i等于0，因为最后一条边，也就是存边时第一条边，在把head值存进next时，head还没有更新过，也就是0。所以当next返回0时，就说明这些边遍历完毕了。

优势与特点

比起邻接矩阵，链式前向星的空间复杂度是O（m），大大节省了存储空间，因为按边存储省掉了很多两点无边的空间。并且在遍历的时候，那些与起点无边相连的点也不需要进行处理，可以说时间和空间都占优势，这就是被OIer们广泛使用的原因。